深度学习与TensorFlow2

环境（版本需要匹配）：

TensorFlow：TensorFlow2.0 GPU版本
Anaconda：4.8.1（conda -V，conda -list，Python 3.7 version），链接：https://www.anaconda.com/distribution/#download-section
CUDA：V10.0.130（nvcc -V），链接：https://developer.nvidia.com/cuda-toolkit-archive
- cuDNN：，链接：https://developer.nvidia.com/rdp/cudnn-archive

一、TensorFlow2基础操作

TensorFlow中的数据载体叫做张量（Tensor）对象，即tf.Tensor，对应不同的类型，能够存储大量的连续的数据。同时所有的运算操作(Operation，简称 OP)也都是基于张量对象进行的

什么是Tensor：

Tensor是一个比较广泛的数据
标量（scalar）：1.1、2.2等准确的数据类型（维度dim=0）
向量（vector）：[1.1]、[1.1,2.2,…]（dim=1）
矩阵（matrix）：[[1.1,2.2],[2.2,2.2],[3.3,2.2]]
数学上tensor：一般指维度>2时的数据，但是在TensorFlow中维度>=1时的数据全称为tensor，甚至标量也可以看作是tensor，所以工程上讲tensor一般指所有的数据

1、数据类型

1.数值类型

数值类型的张量是 TensorFlow 的主要数据载体，根据维度数来区分，可分为：

标量(Scalar)：单个的实数，如 1.2, 3.4 等，维度(Dimension)数为 0， shape 为[]
向量(Vector)：单个实数的有序集合，通过中括号包裹，如[1.2]， [1.2, 3.4]等，维度数为 1，长度不定， shape 为[n]
矩阵(Matrix)：n行m列实数的有序集合，如[[1,2], [3,4]]，也可以写成 $\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}$ ，维度数为 2，每个维度上的长度不定， shape 为[n,m]
张量(Tensor)：所有维度数dim > 2的数组统称为张量。张量的每个维度也作轴(Axis)，一般来说，维度代表了具体的物理含义，张量的维度数以及每个维度所代表的具体物理含义需要由用户自行定义。

比如 Shape 为[2,32,32,3]的张量共有 4 维，如果表示图片数据的话，每个维度/轴代表的含义分别是图片数量、图片高度、图片宽度、图片通道数，其中 2 代表了 2 张图片， 32 代表了高、宽均为 32， 3 代表了 RGB 共 3 个通道

在 TensorFlow 中，为了表达方便，一般把标量、向量、矩阵也统称为张量，不作区分，需要根据张量的维度数或形状自行判断

张量的创建：

>>> import tensorflow as tf
>>> aa = tf.constant(1.2) # TF方式创建标量
>>> x = tf.constant([1,2.,3.3]) # TF方式创建向量
>>> x
<tf.Tensor: id=0, shape=(3,), dtype=float32, numpy=array([1. , 2. , 3.3],dtype=float32)>
>>> a = tf.constant([[1,2],[3,4]]) # TF方式创建2行2列的矩阵
>>> a
<tf.Tensor: id=1, shape=(2, 2), dtype=int32, numpy=
array([[1, 2],
       [3, 4]])>
>>> a = tf.constant([[[1,2],[3,4]],[[5,6],[7,8]]])# TF方式创建3维张量
>>> a
<tf.Tensor: id=2, shape=(2, 2, 2), dtype=int32, numpy=
array([[[1, 2],
        [3, 4]],

       [[5, 6],
        [7, 8]]])>

id：TensorFlow 中内部索引对象的编号
shape：张量的形状
dtype：张量的数值精度

张量可以通过 numpy()方法可以返回 Numpy.array 类型的数据，方便导出数据到系统的其他模块
1
2
>>> x.numpy() # 将 TF 张量的数据导出为 numpy 数组格式
array([1. , 2. , 3.3], dtype=float32)

2.字符串类型

使用频率较低。通过传入字符串对象即可创建字符串类型的张量：

1
2
3

>>> a = tf.constant('Hello, Deep Learning.') # 创建字符串
>>> a
<tf.Tensor: id=3, shape=(), dtype=string, numpy=b'Hello, Deep Learning.'>

在 tf.strings 模块中，提供了常见的字符串类型的工具函数，如小写化 lower()、拼接join()、长度 length()、切分 split()等

将字符串全部小写化：

1 2	>>> tf.strings.lower(a) # 小写化字符串 <tf.Tensor: id=19, shape=(), dtype=string, numpy=b'hello, deep learning.'>

3.布尔类型

布尔类型的张量需要传入 Python 语言的布尔类型数据，转换成 TensorFlow 内部布尔型即可：

>>> a = tf.constant(True) # 创建布尔类型标量
<tf.Tensor: id=22, shape=(), dtype=bool, numpy=True>
>>> a = tf.constant([True, False]) # 创建布尔类型向量
<tf.Tensor: id=25, shape=(2,), dtype=bool, numpy=array([ True, False])>

TensorFlow 的布尔类型和 Python 语言的布尔类型并不等价，不能通用

2、数值精度

保存的数据位越长，精度越高，同时占用的内存空间也就越大。常用的精度类型有tf.int16、tf.int32、tf.int64、tf.float16、tf.float32、tf.float64等，其中tf.float64即为tf.double

在创建张量时，可以指定张量的保存精度：

1 2	>>> tf.constant(123456789, dtype=tf.int16) >>> tf.constant(123456789, dtype=tf.int32)

对于大部分深度学习算法，一般使用 tf.int32 和 tf.float32 可满足大部分场合的运算精度要求，部分对精度要求较高的算法，如强化学习某些算法，可以选择使用 tf.int64 和 tf.float64 精度保存张量

1.读取精度

通过访问张量的dtype成员属性可以判断张量的保存精度

print('before:',a.dtype) # 读取原有张量的数值精度
if a.dtype != tf.float32: # 如果精度不符合要求，则进行转换
    a = tf.cast(a,tf.float32) # tf.cast 函数可以完成精度转换
print('after :',a.dtype) # 打印转换后的精度

2.类型转换

通常通过tf.cast函数进行转换：

1
2
3

>>> a = tf.constant(np.pi, dtype=tf.float16) # 创建 tf.float16 低精度张量
>>> tf.cast(a, tf.double) # 转换为高精度张量
<tf.Tensor: id=44, shape=(), dtype=float64, numpy=3.140625>

布尔类型与整型之间相互转换也是合法的：

1
2
3

>>> a = tf.constant([True, False])
>>> tf.cast(a, tf.int32) # 布尔类型转整型
<tf.Tensor: id=48, shape=(2,), dtype=int32, numpy=array([1, 0])>

一般默认 0 表示 False， 1 表示 True，在 TensorFlow 中，将非 0 数字都视为 True

3、待优化张量

为了区分需要计算梯度信息的张量与不需要计算梯度信息的张量， TensorFlow 增加了
一种专门的数据类型来支持梯度信息的记录：tf.Variable

tf.Variable类型在普通的张量类型基础上添加了 name， trainable 等属性来支持计算图的构建。由于梯度运算会消耗大量的计算资源，而且会自动更新相关参数，对于不需要的优化的张量，如神经网络的输入X，不需要通过 tf.Variable 封装；相反，对于需要计算梯度并优化的张量，如神经网络层的W和b，需要通过 tf.Variable 包裹以便TensorFlow 跟踪相关梯度信息。

通过tf.Variable()函数可以将普通张量转换为待优化张量：

>>> a = tf.constant([-1, 0, 1, 2]) # 创建 TF 张量
>>> aa = tf.Variable(a) # 转换为 Variable 类型
>>> aa.name, aa.trainable # Variable 类型张量的属性
('Variable:0', True)

name 属性：命名计算图中的变量，这套命名体系是 TensorFlow 内部维护的，一般不需要用户关注 name 属性
trainable属性：当前张量是否需要被优化（创建 Variable 对象时默认启用优化标志，可以设置trainable=False来设置张量不需要优化）

直接创建待优化张量：

>>> a = tf.Variable([[1,2],[3,4]]) # 直接创建 Variable 张量
<tf.Variable 'Variable:0' shape=(2, 2) dtype=int32, numpy=
array([[1, 2],
       [3, 4]])>

待优化张量可视为普通张量的特殊类型，普通张量其实也可以通过GradientTape.watch()方法临时加入跟踪梯度信息的列表，从而支持自动求导功能

4、创建张量

1.从数组、列表中创建

通过tf.convert_to_tensor函数可以创建新 Tensor，并将保存在 Python List 对象或者Numpy Array 对象中的数据导入到新 Tensor 中：

>>> tf.convert_to_tensor([1,2.]) # 从列表创建张量
<tf.Tensor: id=86, shape=(2,), dtype=float32, numpy=array([1., 2.],
dtype=float32)>
>>> tf.convert_to_tensor(np.array([[1,2.],[3,4]])) # 从数组中创建张量
<tf.Tensor: id=88, shape=(2, 2), dtype=float64, numpy=
array([[1., 2.],
       [3., 4.]])>

Numpy 浮点数数组默认使用 64 位精度保存数据，可以在需要的时候将其转换为 tf.float32 类型
实际上， tf.constant()和 tf.convert_to_tensor()都能够自动的把 Numpy 数组或者 Python列表数据类型转化为 Tensor 类型，这两个 API 命名来自 TensorFlow 1.x 的命名习惯，在TensorFlow 2 中函数的名字并不是很贴切，使用其一即可

2.创建全0全1张量

通过tf.zeros()和tf.ones()可创建任意形状，且内容全 0 或全 1 的张量：

>>> tf.zeros([]),tf.ones([]) # 创建全 0，全 1 的标量
(<tf.Tensor: id=90, shape=(), dtype=float32, numpy=0.0>,
<tf.Tensor: id=91, shape=(), dtype=float32, numpy=1.0>)

>>> tf.zeros([1]),tf.ones([1]) # 创建全 0，全 1 的向量
(<tf.Tensor: id=96, shape=(1,), dtype=float32, numpy=array([0.],
dtype=float32)>,
<tf.Tensor: id=99, shape=(1,), dtype=float32, numpy=array([1.],
dtype=float32)>)

>>> tf.ones([3,2]) # 创建全 1 矩阵，指定 shape 为 3 行 2 列
<tf.Tensor: id=108, shape=(3, 2), dtype=float32, numpy=
array([[1., 1.],
       [1., 1.],
       [1., 1.]], dtype=float32)>

通过tf.zeros_like、tf.ones_like可以方便地新建与某个张量 shape 一致，且内容为全 0 或全 1 的张量：

>>> a = tf.ones([2,3]) # 创建一个矩阵
>>> tf.zeros_like(a) # 创建一个与 a 形状相同，但是全 0 的新矩阵
<tf.Tensor: id=113, shape=(2, 3), dtype=float32, numpy=
array([[0., 0., 0.],
       [0., 0., 0.]], dtype=float32)>

tf.*_like是一系列的便捷函数，可以通过tf.zeros(a.shape)等方式实现

3.创建自定义数值张量

通过tf.fill(shape, value)可以创建全为自定义数值 value 的张量，形状由 shape 参数指定：

>>> tf.fill([2,2], 99) # 创建 2 行 2 列，元素全为 99 的矩阵
<tf.Tensor: id=136, shape=(2, 2), dtype=int32, numpy=
array([[99, 99],
       [99, 99]])>

4.创建已知分布的张量

通过tf.random.normal(shape, mean=0.0, stddev=1.0)可以创建形状为 shape，均值为mean，标准差为 stddev 的正态分布：

>>> tf.random.normal([2,2]) # 创建标准正态分布的张量
<tf.Tensor: id=143, shape=(2, 2), dtype=float32, numpy=
array([[-0.4307344 , 0.44147003],
       [-0.6563149 , -0.30100572]], dtype=float32)>

通过tf.random.uniform(shape, minval=0, maxval=None, dtype=tf.float32)可以创建采样自[minval, maxval)区间的均匀分布的张量：

>>> tf.random.uniform([2,2]) # 创建采样自[0,1)均匀分布的矩阵
<tf.Tensor: id=158, shape=(2, 2), dtype=float32, numpy=
array([[0.65483284, 0.63064325],
       [0.008816 , 0.81437767]], dtype=float32)>

5.创建序列

tf.range(limit, delta=1)可以创建[0, limit)之间，步长为 delta 的整型序列，不包含 limit 本身：

1 2	>>> tf.range(10) # 0~10，不包含 10 <tf.Tensor: id=180, shape=(10,), dtype=int32, numpy=array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])>

通过tf.range(start, limit, delta=1)可以创建[start, limit)，步长为 delta 的序列，不包含limit 本身

1 2	>>> tf.range(1,10,delta=2) # 1~10 <tf.Tensor: id=190, shape=(5,), dtype=int32, numpy=array([1, 3, 5, 7, 9])>

5、张量的典型用途

标量：误差值的表示、各种测量指标的表示，比如准确度(Accuracy，简称 acc)，精度(Precision)和召回率(Recall)等

向量：如在全连接层和卷积神经网络层中，偏置张量b就是使用向量来表示

矩阵：比如全连接层的批量输入张量X的形状为[b,din]，其中b表示输入样本的个数，即Batch Size，din表示输入特征的长度

三维张量：表示序列信号，它的格式是 $X=[b,sequence,feature\ len]$ ，其中b表示序列信号的数量， sequence len 表示序列信号在时间维度上的采样点数或步数，feature len 表示每个点的特征长度，自然语言处理(Natural Language Processing，简称 NLP)中会使用到

四维张量：卷积神经网络中应用广泛，用于保存特征图数据，格式一般为 $[b,h,w,c]$ ，其中b表示输入样本的数量， h/w 分别表示特征图的高/宽，c表示特征图的通道数。部分深度学习框架（如PyTorch）会使用 $[b,c,h,w]$ 格式

大于四维的张量一般应用的比较少，如在元学习(Meta Learning)中会采用五维的张量表示方法，理解方法与三、四维张量类似

6、索引与切片

1.索引

在 TensorFlow 中，支持基本的 $[i][j]...$ 标准索引方式，也支持通过逗号分隔索引号的索引方式

>>> x = tf.random.normal([4,32,32,3]) # 创建 4D 张量（4张32*32大小的彩色图片）
>>> x[0] # 程序中的第一的索引号应为 0，容易混淆，不过不影响理解
<tf.Tensor: id=379, shape=(32, 32, 3), dtype=float32, numpy=
array([[[ 1.3005302 , 1.5301839 , -0.32005513],
        [-1.3020388 , 1.7837263 , -1.0747638 ], ...
        [-1.1092019 , -1.045254 , -0.4980363 ],
        [-0.9099222 , 0.3947732 , -0.10433522]]], dtype=float32)>
>>> x[2][1][0][1] # 取第 3 张图片，第 2 行，第 1 列的像素， B 通道(第 2 个通道)颜色强度值
<tf.Tensor: id=418, shape=(), dtype=float32, numpy=-0.84922135>

当张量的维度数较高时，使用 $[i][j]...[k]$ 的方式书写不方便，可以采用 $[i,j,...,k]$ 方式索引，他们是等价的：

1
2

>>> x[1,9,2] # 取第 2 张图片，第 10 行，第 3 列的数据，实现如下
<tf.Tensor: id=436, shape=(3,), dtype=float32, numpy=array([ 1.7487534 , -0.41491988, -0.2944692 ], dtype=float32)>

2.切片

通过start:end:step切片方式可以方便地提取一段数据，其中 start 为开始读取位置的索引， end 为结束读取位置的索引(不包含 end 位)， step 为采样步长

>>> x[1:3] # 读取第 2,3 张图片
<tf.Tensor: id=441, shape=(2, 32, 32, 3), dtype=float32, numpy=
array([[[[ 0.6920027 , 0.18658352, 0.0568333 ],
         [ 0.31422952, 0.75933754, 0.26853144],
         [ 2.7898 , -0.4284912 , -0.26247284],...

start:end:step切片方式有很多简写方式

全部省略时即为::，表示从最开始读取到最末尾，步长为 1（不跳过任何元素）。为了更加简洁， ::可以简写为单个冒号:
从第一个元素读取时start可以省略（即start=0可以省略）
取到最后一个元素时end可以省略
步长为 1 时step可以省略

特别地，step可以为负数，当step = -1时，start:end:-1表示从 start 开始，逆序读取至 end 结束(不包含 end)，索引号 $end\leqslant start$

>>> x = tf.range(9) # 创建 0~9 向量
>>> x[8:0:-1] # 从 8 取到 0，逆序，不包含 0
<tf.Tensor: id=466, shape=(8,), dtype=int32, numpy=array([8, 7, 6, 5, 4, 3, 2, 1])>
>>> x = tf.random.normal([4,32,32,3])
>>> x[0,::-2,::-2] # 行、列逆序间隔采样
<tf.Tensor: id=487, shape=(16, 16, 3), dtype=float32, numpy=
array([[[ 0.63320625, 0.0655185 , 0.19056146],
        [-1.0078577 , -0.61400175, 0.61183935],
        [ 0.9230892 , -0.6860094 , -0.01580668],
        ...

为了避免出现像 [: , : , : ,1]这样过多冒号的情况，可以使用...符号表示取多个维度上所有的数据，其中维度的数量需根据规则自动推断：

当切片方式出现...符号时，...符号左边的维度将自动对齐到最左边
...符号右边的维度将自动对齐到最右边，此时系统再自动推断...符号代表的维度数量

>>> x = tf.random.normal([4,32,32,3])
>>> x[0:2,...,1:] # 高宽维度全部采集
<tf.Tensor: id=497, shape=(2, 32, 32, 2), dtype=float32, numpy=
array([[[[ 0.575703 , 0.8872789 ],
         [ 0.11028383, -0.27128693],
         [-0.9950867 , -1.7737272 ],
         ...

7、维度变换

算法的每个模块对于数据张量的格式有不同的逻辑要求，当现有的数据格式不满足算法要求时，需要通过维度变换将数据调整为正确的格式。这就是维度变换的功能。

基本的维度变换操作函数包含了改变视图 reshape、插入新维度 expand_dims，删除维度 squeeze、交换维度 transpose、复制数据 tile 等函数

Batch 维度：为了实现维度变换，我们需要将原始数据插入一个新的维度，并把它定义为 Batch 维度，然后在 Batch 维度对数据进行相关操作，得到变换后的新的数据。这一系列的操作就是维度变换操作。

1.改变视图 reshape

张量的视图（View）：就是我们理解张量的方式，比如 shape 为[2,4,4,3]的张量A，从逻辑上可以理解为 2 张图片，每张图片 4 行 4 列，每个位置有 RGB 3 个通道的数据

张量的存储（Storage）：体现在张量在内存上保存为一段连续的内存区域，对于同样的存储，我们可以有不同的理解方式，比如上述张量A，我们可以在不改变张量的存储下，将张量A理解为 2个样本，每个样本的特征为长度 48 的向量

同一个存储，从不同的角度观察数据，可以产生不同的视图，这就是存储与视图的关系。视图的产生是非常灵活的，但需要保证是合理。

通过 tf.range()模拟生成一个向量数据，并通过tf.reshape视图改变函数产生不同的视图：

>>> x=tf.range(96) # 生成向量
>>> x=tf.reshape(x,[2,4,4,3]) # 改变 x 的视图，获得 4D 张量，存储并未改变
# 可以观察到数据仍然是 0~95 的顺序，可见数据并未改变，改变的是数据的结构
<tf.Tensor: id=11, shape=(2, 4, 4, 3), dtype=int32, numpy=
array([[[[ 0, 1, 2],
         [ 3, 4, 5],
         [ 6, 7, 8],
         [ 9, 10, 11]],...

在存储数据时，内存只能以平铺方式按序写入内存，因此视图的层级关系需要人为管理。为了方便表达，一般把张量 shape 列表中相对靠左侧的维度叫作大维度， shape 列表中相对靠右侧的维度叫作小维度（如[2,4,4,3]的张量中，图片数量维度与通道数量相比，图片数量叫作大维度，通道数叫作小维度）

改变视图操作在提供便捷性的同时，也会带来很多逻辑隐患，主要的原因是改变视图操作的默认前提是存储不需要改变，否则改变视图操作就是非法的

张量A按着初始视图[b,h,w,c]写入的内存布局，改变A的理解方式，它可以有多种合法的理解方式：

[b,h∙w,c]张量理解为b张图片，h∙w个像素点，c个通道

[b,h,w∙c]张量理解为b张图片，h行，每行的特征长度为w∙c

[b,h∙w∙c]张量理解为b张图片，每张图片的特征长度为h∙w∙c

从语法上来说，视图变换只需要满足新视图的元素总量与存储区域大小相等即可。正是由于视图的设计的语法约束很少，使得在改变视图时容易出现逻辑隐患。

不合法的视图变换：

例如，如果定义新视图为[b,w,h,c]，[b,c,h*w]或者[b,c,h,w]等时，张量的存储顺序需要改变，如果不同步更新张量的存储顺序，那么恢复出的数据将与新视图不一致，从而导致数据错乱。

这需要用户理解数据，才能判断操作是否合法。我们会在“交换维度”一节介绍如何改变张量的存储

在通过 reshape 改变视图时，必须始终记住张量的存储顺序，新视图的维度顺序不能与存储顺序相悖，否则需要通过交换维度操作将存储顺序同步过来

在 TensorFlow 中，可以通过张量的 ndim 和 shape 成员属性获得张量的维度数和形状：

1 2	>>> x.ndim,x.shape # 获取张量的维度数和形状列表 (4, TensorShape([2, 4, 4, 3]))

通过 tf.reshape(x, new_shape)，可以将张量的视图任意地合法改变：

>>> tf.reshape(x,[2,-1])
<tf.Tensor: id=520, shape=(2, 48), dtype=int32, numpy=
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,
        16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,…
        80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95]])>

参数-1：当前轴上长度需要根据张量总元素不变的法则自动推导（该处推导成(2*4*4*3)/2=48）

再次改变数据的视图为[2,16,3] ，实现如下：

>>> tf.reshape(x,[2,-1,3])
<tf.Tensor: id=526, shape=(2, 16, 3), dtype=int32, numpy=
array([[[ 0, 1, 2], …
       [45, 46, 47]],
      [[48, 49, 50],…
       [93, 94, 95]]])>

上述一系列连续变换视图操作中，张量的存储顺序始终没有改变，数据在内存中仍然是按着初始写入的顺序0,1,2, ⋯ ,95保存

2.增删维度

增加维度

通过 tf.expand_dims(x, axis)可在指定的 axis 轴前可以插入一个新的维度（长度为1）：

>>> x = tf.random.uniform([28,28],maxval=10,dtype=tf.int32) # 产生矩阵
<tf.Tensor: id=11, shape=(28, 28), dtype=int32, numpy=
array([[6, 2, 0, 0, 6, 7, 3, 3, 6, 2, 6, 2, 9, 3, 0, 3, 2, 8, 1, 3, 6, 2, 3, 9, 3, 6, 1, 7],...
>>> x = tf.expand_dims(x,axis=2) # axis=2 表示宽维度后面的一个维度
<tf.Tensor: id=13, shape=(28, 28, 1), dtype=int32, numpy=
array([[[6],
        [2],
        [0],
        [0],
        [6],
        [7],
        [3],...

增加一个长度为 1 的维度相当于给原有的数据添加一个新维度的概念，数据并不发生改变，仅仅是改变数据的理解方式，因此它其实可以理解为改变视图的一种特殊方式

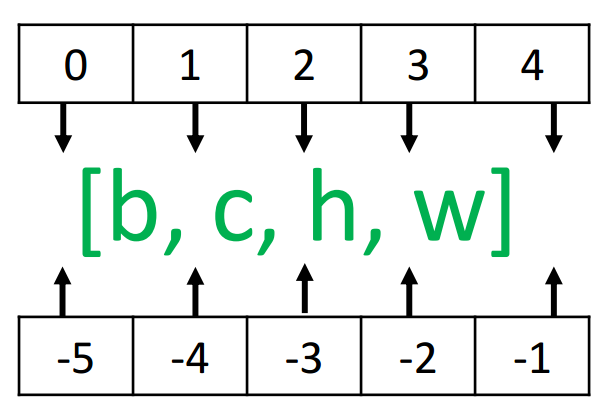
需要注意的是， tf.expand_dims 的 axis 为正时，表示在当前维度之前插入一个新维度；为负时，表示当前维度之后插入一个新的维度。以[b,h,w,c]张量为例，不同 axis 参数的实际插入位置如下所示：

增加维度 axis 参数位置示意图

删除维度

与增加维度一样，删除维度只能删除长度为1的维度，也不会改变张量的存储。

通过 tf.squeeze(x, axis)函数， axis 参数为待删除的维度的索引号：

#数据同上一个例子
>>> x = tf.squeeze(x, axis=2) # 删除图片通道数维度
<tf.Tensor: id=588, shape=(28, 28), dtype=int32, numpy=
array([[8, 2, 2, 0, 7, 0, 1, 4, 9, 1, 7, 4, 8, 2, 7, 4, 8, 2, 9, 8, 8, 0, 9, 9, 7, 5, 9, 7],
       [3, 4, 9, 9, 0, 6, 5, 7, 1, 9, 9, 1, 2, 7, 2, 7, 5, 3, 3, 7, 2, 4, 5, 2, 7, 3, 8, 0],...

如果不指定维度参数 axis，即 tf.squeeze(x)，那么它会默认删除所有长度为 1 的维度

3.交换维度

在保持维度顺序不变的条件下，仅仅改变张量的理解方式是不够的，有时需要直接调整的存储顺序，即交换维度(Transpose)。通过交换维度操作，改变了张量的存储顺序，同时也改变了张量的视图

以图片格式[b,h,w,c]转换到图片格式[b,c,h,w]为例，介绍使用 tf.transpose(x, perm)函数完成维度交换操作，其中参数 perm表示新维度的顺序 List。

>>> x = tf.random.normal([2,32,32,3])
>>> tf.transpose(x,perm=[0,3,1,2]) # 交换维度
<tf.Tensor: id=603, shape=(2, 3, 32, 32), dtype=float32, numpy=
array([[[[-1.93072677e+00, -4.80163872e-01, -8.85614634e-01, ...,
          1.49124235e-01, 1.16427064e+00, -1.47740364e+00],
         [-1.94761145e+00, 7.26879001e-01, -4.41877693e-01, ...

图片张量 shape 为[2,32,32,3]，“图片数量、行、列、通道数” 的维度索引分别为 0、 1、 2、 3。交换为[b,c,h,w]格式，新维度的排序为“图片数量、通道数、行、列”，对应的索引号为[0,3,1,2]
通过 tf.transpose 维度交换后，张量的存储顺序已经改变，视图也随之改变，后续的所有操作必须基于新的存续顺序和视图进行。相对于改变视图操作，维度交换操作的计算代价更高

4.复制数据

可以通过tf.tile(x, multiples)函数完成数据在指定维度上的复制操作， multiples 分别指定了每个维度上面的复制倍数，对应位置为 1 表明不复制，为 2 表明新长度为原来长度的2 倍，即数据复制一份，以此类推

>>> b = tf.constant([1,2]) # 创建向量 b
>>> b = tf.expand_dims(b, axis=0) # 插入新维度，变成矩阵
<tf.Tensor: id=645, shape=(1, 2), dtype=int32, numpy=array([[1, 2]])>
# 在 Batch 维度上复制数据 1 份，实现如下：
>>> b = tf.tile(b, multiples=[2,1]) # 样本维度上复制一份
<tf.Tensor: id=648, shape=(2, 2), dtype=int32, numpy=
array([[1, 2],
       [1, 2]])>

tf.tile 会创建一个新的张量来保存复制后的张量，会涉及大量数据的读写 IO 运算，计算代价相对较高

8、Broadcasting

Broadcasting 称为广播机制(或自动扩展机制)，它是一种轻量级的张量复制手段，在逻辑上扩展张量数据的形状，但是只会在需要时才会执行实际存储复制操作。

对于用户来说， Broadcasting 和 tf.tile 复制的最终效果是一样的，操作对用户透明，但是 Broadcasting 机制节省了大量计算资源，建议在运算过程中尽可能地利用 Broadcasting 机制提高计算效率

考虑一个例子： $Y=X@W+b$ ，其中 $X@W$ 的 shape 为[2,3]，b的 shape 为[3]，可以通过结合 tf.expand_dims 和 tf.tile 手动完成复制数据操作，将b变换为[2,3]，然后与 $X@W$ 完成相加运算。但实际上，直接将 shape 为[2,3]与[3]的b相加也是合法的，例如：

>>> x = tf.random.normal([2,4])
>>> w = tf.random.normal([4,3])
>>> b = tf.random.normal([3])
>>> y = x@w+b # 不同 shape 的张量直接相加

会自动调用 Broadcasting函数 tf.broadcast_to(x, new_shape)，将两者 shape 扩张为相同的[2,3]，即上式可以等效为
1
>>> y = x@w + tf.broadcast_to(b,[2,3]) # 手动扩展，并相加
操作符+在遇到 shape 不一致的 2 个张量时，会自动考虑将 2 个张量自动扩展到一致的 shape，然后再调用 tf.add 完成张量相加运算

所有的运算都需要在正确逻辑（满足Broadcasting 设计的核心思想）下进行， Broadcasting 机制并不会扰乱正常的计算逻辑，它只会针对于最常见的场景自动完成增加维度并复制数据的功能，提高开发效率和运行效率。

Broadcasting 机制的核心思想是普适性，即同一份数据能普遍适合于其他位置。在验证普适性之前，需要先将张量 shape 靠右对齐，然后进行普适性判断：

对于长度为1的维度，默认这个数据普遍适合于当前维度的其他位置

对于不存在的维度，则在增加新维度后默认当前数据也是普适于新维度的，从而可以扩展为更多维度数、任意长度的张量形状

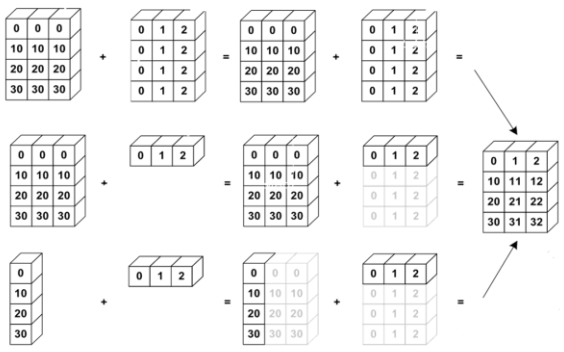
在进行张量运算时，有些运算在处理不同 shape 的张量时，会隐式地自动调用Broadcasting 机制，如+， -， *， /等运算，将参与运算的张量 Broadcasting 成一个公共shape，再进行相应的计算。

加法运算时自动Broadcasting示意图

1
2
3

>>> a = tf.random.normal([2,32,32,1])
>>> b = tf.random.normal([32,32])
>>> a+b,a-b,a*b,a/b # 测试加减乘除运算的 Broadcasting 机制

这些运算都能 Broadcasting 成[2,32,32,32]的公共 shape，再进行运算

9、数学运算

1.加减乘除

加、减、乘、除是最基本的数学运算，分别通过 tf.add, tf.subtract, tf.multiply, tf.divide函数实现， TensorFlow 已经重载了+、 - 、 ∗ 、 /运算符，推荐直接使用运算符来完成加、减、乘、除运算

整除和余除也是常见的运算之一，分别通过//和%运算符实现

>>> a = tf.range(5)
>>> b = tf.constant(2)
>>> a//b # 整除运算
<tf.Tensor: id=115, shape=(5,), dtype=int32, numpy=array([0, 0, 1, 1, 2])>
>>> a%b # 余除运算
<tf.Tensor: id=117, shape=(5,), dtype=int32, numpy=array([0, 1, 0, 1, 0])>

2.乘方

通过 tf.pow(x, a)可以方便地完成 $y=x^a$ 的乘方运算，也可以通过运算符**实现x∗∗a运算：

>>> x = tf.range(4)
>>> tf.pow(x,3) # 乘方运算
<tf.Tensor: id=124, shape=(4,), dtype=int32, numpy=array([ 0, 1, 8, 27])>

>>> x**2 # 乘方运算符
<tf.Tensor: id=127, shape=(4,), dtype=int32, numpy=array([0, 1, 4, 9])>

>>> x=tf.constant([1.,4.,9.])
>>> x**(0.5) # 平方根
<tf.Tensor: id=139, shape=(3,), dtype=float32, numpy=array([1., 2., 3.], dtype=float32)>

设置指数为 $\frac{1}{a}$ 形式，即可实现 $\sqrt[a]{x}$ 根号运算
对于常见的平方和平方根运算，可以使用 tf.square(x)和 tf.sqrt(x)实现

3.指数和对数

通过 tf.pow(a, x)或者**运算符也可以方便地实现指数运算 $a^x$

>>> x = tf.constant([1.,2.,3.])
>>> 2**x # 指数运算
<tf.Tensor: id=179, shape=(3,), dtype=float32, numpy=array([2., 4., 8.], dtype=float32)>

>>> tf.exp(1.) # 自然指数运算
<tf.Tensor: id=182, shape=(), dtype=float32, numpy=2.7182817>

对于自然指数 $e^x$ ，可以通过 tf.exp(x)实现

自然对数 $log_ex$ 可以通过 tf.math.log(x)实现：

1
2
3

>>> x=tf.exp(3.)
>>> tf.math.log(x) # 对数运算
<tf.Tensor: id=186, shape=(), dtype=float32, numpy=3.0>

如果希望计算其它底数的对数，可以根据对数的换底公式 $log_ax=\frac{log_ex}{log_ea}$ 间接实现

>>> x = tf.constant([1.,2.])
>>> x = 10**x
>>> tf.math.log(x)/tf.math.log(10.) # 换底公式
<tf.Tensor: id=6, shape=(2,), dtype=float32, numpy=array([1., 2.], dtype=float32)>

4.矩阵乘法

通过@运算符可以方便的实现矩阵相乘，还可以通过 tf.matmul(a, b)函数实现

需要注意的是， TensorFlow 中的矩阵相乘可以使用批量方式，也就是张量A和B的维度数可以大于 2。当张量A和B维度数大于 2 时， TensorFlow 会选择A和B的最后两个维度进行矩阵相乘，前面所有的维度都视作Batch 维度

>>> a = tf.random.normal([4,3,28,32])
>>> b = tf.random.normal([4,3,32,2])
>>> a@b # 批量形式的矩阵相乘
<tf.Tensor: id=236, shape=(4, 3, 28, 2), dtype=float32, numpy=
array([[[[-1.66706240e+00, -8.32602978e+00],
         [ 9.83304405e+00, 8.15909767e+00],
         [ 6.31014729e+00, 9.26124632e-01],...

矩阵相乘函数同样支持自动 Broadcasting 机制

>>> a = tf.random.normal([4,28,32])
>>> b = tf.random.normal([32,16])
>>> tf.matmul(a,b) # 先自动扩展，再矩阵相乘
<tf.Tensor: id=264, shape=(4, 28, 16), dtype=float32, numpy=
array([[[-1.11323869e+00, -9.48194981e+00, 6.48123884e+00, ...,
         6.53280640e+00, -3.10894990e+00, 1.53050375e+00],
        [ 4.35898495e+00, -1.03704405e+01, 8.90656471e+00, ...,

二、TensorFlow2进阶操作

1、合并与分割

1.合并

合并：将多个张量在某个维度上合并为一个张量

张量的合并可以使用拼接(Concatenate)和堆叠(Stack)操作实现：

拼接：不会产生新的维度，仅在现有的维度上合并
堆叠：会创建新维度

选择使用拼接还是堆叠操作来合并张量，取决于具体的场景是否需要创建新维度

拼接

通过tf.concat(tensors, axis)函数拼接张量，其中参数tensors 保存了所有需要合并的张量 List， axis 参数指定需要合并的维度索引

>>> a = tf.random.normal([4,35,8]) # 模拟成绩册 A
>>> b = tf.random.normal([6,35,8]) # 模拟成绩册 B
>>> tf.concat([a,b],axis=0) # 拼接合并成绩册
<tf.Tensor: id=13, shape=(10, 35, 8), dtype=float32, numpy=
array([[[ 1.95299834e-01, 6.87859178e-01, -5.80048323e-01, ...,
          1.29430830e+00, 2.56610274e-01, -1.27798581e+00],
        [ 4.29753691e-01, 9.11329567e-01, -4.47975427e-01, ...,

从语法上来说，拼接合并操作可以在任意的维度上进行，唯一的约束是非合并维度的长度必须一致

堆叠

使用tf.stack(tensors, axis)可以堆叠方式合并多个张量，通过 tensors 列表表示，参数axis 指定新维度插入的位置（用法与 tf.expand_dims 一致，当axis ≥ 0时，在 axis之前插入；当axis < 0时，在 axis 之后插入新维度）

>>> a = tf.random.normal([35,8])
>>> b = tf.random.normal([35,8])
>>> tf.stack([a,b],axis=0) # 堆叠合并为 2 个班级，班级维度插入在最前
<tf.Tensor: id=55, shape=(2, 35, 8), dtype=float32, numpy=
array([[[ 3.68728966e-01, -8.54765773e-01, -4.77824420e-01,
         -3.83714020e-01, -1.73216307e+00, 2.03872994e-02,
          2.63810277e+00, -1.12998331e+00],...

需要所有待合并的张量 shape 完全一致才可合并

2.分割

合并操作的逆过程就是分割，将一个张量分拆为多个张量

通过tf.split(x, num_or_size_splits, axis)可以完成张量的分割操作

x：待分割张量
num_or_size_splits：切割方案。当 num_or_size_splits 为单个数值时，如 10，表
示等长切割为 10 份；当 num_or_size_splits 为 List 时， List 的每个元素表示每份的长度，如[2,4,2,2]表示切割为 4 份，每份的长度依次是 2、 4、 2、 2
axis：指定分割的维度索引号

>>> x = tf.random.normal([10,35,8])
# 等长切割为 10 份
>>> result = tf.split(x, num_or_size_splits=10, axis=0)
>>> len(result) # 返回的列表为 10 个张量的列表
10
>>> result[0] # 查看第一个班级的成绩册张量
<tf.Tensor: id=136, shape=(1, 35, 8), dtype=float32, numpy=
array([[[-1.7786729 , 0.2970506 , 0.02983334, 1.3970423 ,
          1.315918 , -0.79110134, -0.8501629 , -1.5549672 ],
        [ 0.5398711 , 0.21478991, -0.08685189, 0.7730989 ,...

仍保留了第一个维度

如果希望在某个维度上全部按长度为 1 的方式分割，还可以使用tf.unstack(x, axis)函数。这种方式是tf.split的一种特殊情况，切割长度固定为 1，只需要指定切割维度的索引号即可

>>> x = tf.random.normal([10,35,8])
>>> result = tf.unstack(x,axis=0) # Unstack 为长度为 1 的张量
>>> len(result) # 返回 10 个张量的列表
10
>>> result[0] # 第一个班级
<tf.Tensor: id=166, shape=(35, 8), dtype=float32, numpy=
array([[-0.2034383 , 1.1851563 , 0.25327438, -0.10160723, 2.094969 , -0.8571669 , -0.48985648, 0.55798006],...

通过tf.unstack切割后，shape 变为[35,8]，即第一个维度消失了，这是与tf.split区别之处

2、数据统计

1.向量范数

向量范数(Vector Norm)是表征向量“长度”的一种度量方法，它可以推广到张量上。在神经网络中，常用来表示张量的权值大小，梯度大小等。常用的向量范数有：

L1 范数，定义为向量x的所有元素绝对值之和： $\left \| x \right \|_1=\sum_{i}\left | x_i \right |$
L2 范数，定义为向量x的所有元素的平方和，再开根号： $\left \| x \right \|_2=\sqrt{\sum_{i}\left | x_i \right |^2}$
$\infty$ -范数，定义为向量x的所有元素绝对值的最大值： $\left \| x \right \|_\infty=max_i(\left | x_i \right |)$

对于矩阵和张量，同样可以利用向量范数的计算公式，等价于将矩阵和张量打平成向量后计算

通过tf.norm(x, ord)求解张量的 L1、 L2、 $\infty$ 等范数，其中参数ord 指定为 1、 2时计算 L1、 L2 范数，指定为np.inf时计算 $\infty$ -范数

>>> x = tf.ones([2,2])
>>> tf.norm(x,ord=1) # 计算 L1 范数
<tf.Tensor: id=183, shape=(), dtype=float32, numpy=4.0>

>>> tf.norm(x,ord=2) # 计算 L2 范数
<tf.Tensor: id=189, shape=(), dtype=float32, numpy=2.0>

>>> import numpy as np
>>> tf.norm(x,ord=np.inf) # 计算∞范数
<tf.Tensor: id=194, shape=(), dtype=float32, numpy=1.0>

2.最值、均值、和

通过 tf.reduce_max、 tf.reduce_min、 tf.reduce_mean、 tf.reduce_sum 函数可以求解张量在某个维度上的最大、最小、均值、和，也可以求全局最大、最小、均值、和信息

# 假设第一个维度为样本数量，第二个维度为当前样本分别属于 10 个类别的概率
>>> x = tf.random.normal([4,10]) # 模型生成概率

>>> tf.reduce_max(x,axis=1) # 统计概率维度上的最大值
<tf.Tensor: id=203, shape=(4,), dtype=float32, numpy=array([1.2410722 , 0.88495886, 1.4170984 , 0.9550192 ], dtype=float32)>

>>> tf.reduce_min(x,axis=1) # 统计概率维度上的最小值
<tf.Tensor: id=206, shape=(4,), dtype=float32, numpy=array([-0.27862206, -2.4480672 , -1.9983795 , -1.5287997 ], dtype=float32)>

>>> tf.reduce_mean(x,axis=1) # 统计概率维度上的均值
<tf.Tensor: id=209, shape=(4,), dtype=float32, numpy=array([ 0.39526337, -0.17684573, -0.148988 , -0.43544054], dtype=float32)>

# 统计全局的最大、最小、均值、和，返回的张量均为标量
>>> x = tf.random.normal([4,10]) # 模型生成概率
>>> tf.reduce_max(x),tf.reduce_min(x),tf.reduce_mean(x)
(<tf.Tensor: id=218, shape=(), dtype=float32, numpy=1.8653786>, <tf.Tensor: id=220, shape=(), dtype=float32, numpy=-1.9751656>, <tf.Tensor: id=222, shape=(), dtype=float32, numpy=0.014772797>)

不指定 axis 参数时， tf.reduce_*函数会求解出全局元素的最大、最小、均值、和等数据

通过 tf.argmax(x, axis)和 tf.argmin(x, axis)可以求解在 axis 轴上， x 的最大值、最小值所在的索引号

# out：
<tf.Tensor: id=257, shape=(2, 10), dtype=float32, numpy=
array([[0.18773547, 0.1510464 , 0.09431915, 0.13652141, 0.06579739,
        0.02033597, 0.06067333, 0.0666793 , 0.14594753, 0.07094406],
       [0.5092072 , 0.03887136, 0.0390687 , 0.01911005, 0.03850609,
        0.03442522, 0.08060656, 0.10171875, 0.08244187, 0.05604421]], dtype=float32)>

>>> pred = tf.argmax(out, axis=1) # 选取概率最大的位置
<tf.Tensor: id=262, shape=(2,), dtype=int64, numpy=array([0, 0], dtype=int64)>

3、张量比较

通过tf.equal(a, b)(或tf.math.equal(a, b)，两者等价)函数可以比较2个张量是否相等

# pred：
<tf.Tensor: id=272, shape=(100,), dtype=int64, numpy=
array([0, 6, 4, 3, 6, 8, 6, 3, 7, 9, 5, 7, 3, 7, 1, 5, 6, 1, 2, 9, 0, 6, 5, 4, 9, 5, 6, 4, 6, 0, 8, 4, 7, 3, 4, 7, 4, 1, 2, 4, 9, 4,...
>>> y = tf.random.uniform([100],dtype=tf.int64,maxval=10)
<tf.Tensor: id=281, shape=(100,), dtype=int64, numpy=
array([0, 9, 8, 4, 9, 7, 2, 7, 6, 7, 3, 4, 2, 6, 5, 0, 9, 4, 5, 8, 4, 2, 5, 5, 5, 3, 8, 5, 2, 0, 3, 6, 0, 7, 1, 1, 7, 0, 6, 1, 2, 1, 3,...
>>> out = tf.equal(pred,y) # 预测值与真实值比较，返回布尔类型的张量
<tf.Tensor: id=288, shape=(100,), dtype=bool, numpy=
array([False, False, False, False, True, False, False, False, False, False, False, False, False, False, True, False, False, True,...

4、复制和填充

1.填充

之前我们介绍了通过复制的方式可以增加数据的长度，但是重复复制数据会破坏原有的数据结构，并不适合于此处。通常的做法是，在需要补充长度的数据开始或结束处填充足够数量的特定数值，这些特定数值一般代表了无效意义，例如 0，使得填充后的长度满足系统要求。那么这种操作就叫作填充(Padding)

填充操作可以通过tf.pad(x, paddings)函数实现，参数 paddings 是包含了多个[Left Padding, Right Padding]的嵌套方案 List，如[[0,0], [2,1], [1,2]]表示第一个维度不填充，第二个维度左边(起始处)填充两个单元，右边(结束处)填充一个单元，第三个维度左边填充一个单元，右边填充两个单元

>>> a = tf.constant([1,2,3,4,5,6]) # 第一个句子
>>> b = tf.constant([7,8,1,6]) # 第二个句子
>>> b = tf.pad(b, [[0,2]]) # 句子末尾填充 2 个 0
<tf.Tensor: id=3, shape=(6,), dtype=int32, numpy=array([7, 8, 1, 6, 0, 0])>

2.复制

即tf.tile()函数。参考基础操作->维度变换->复制数据章节

5、数据限幅

可以通过tf.maximum(x, a)实现数据的下限幅，即 $x\in [a,+\infty )$ 。可以通过tf.minimum(x, a)实现数据的上限幅，即 $x\in (-\infty ,a]$

>>> x = tf.range(9)
>>> tf.maximum(x,2) # 下限幅到 2
<tf.Tensor: id=48, shape=(9,), dtype=int32, numpy=array([2, 2, 2, 3, 4, 5, 6, 7, 8])>
>>> tf.minimum(x,7) # 上限幅到 7
<tf.Tensor: id=41, shape=(9,), dtype=int32, numpy=array([0, 1, 2, 3, 4, 5, 6, 7, 7])>

通过组合tf.maximum(x, a)和tf.minimum(x, b)可以实现同时对数据的上下边界限幅，即 $x\in [a,b]$

1
2
3

>>> x = tf.range(9)
>>> tf.minimum(tf.maximum(x,2),7) # 限幅为 2~7
<tf.Tensor: id=57, shape=(9,), dtype=int32, numpy=array([2, 2, 2, 3, 4, 5, 6, 7, 7])>

更方便地，我们可以使用tf.clip_by_value函数实现上下限幅：

1
2
3

>>> x = tf.range(9)
>>> tf.clip_by_value(x,2,7) # 限幅为 2~7
<tf.Tensor: id=66, shape=(9,), dtype=int32, numpy=array([2, 2, 2, 3, 4, 5, 6, 7, 7])>

6、高级操作

1.tf.gather

tf.gather可以实现根据索引号收集数据的目的（与切片类似，但是对于不规则的索引方式，切片实现起来非常麻烦，而tf.gather则更加方便）

参数1：带收集的张量
参数2：指定需要收集的索引号
参数3：指定收集的维度

>>> x = tf.random.uniform([4,35,8],maxval=100,dtype=tf.int32) # 成绩册张量（4个班级 35个学生 8门科目）
# 收集第 1,4,9,12,13,27 号同学成绩
>>> tf.gather(x,[0,3,8,11,12,26],axis=1)
<tf.Tensor: id=87, shape=(4, 6, 8), dtype=int32, numpy=
array([[[43, 10, 93, 85, 75, 87, 28, 19],
        [74, 11, 25, 64, 84, 89, 79, 85],...

索引号可以乱序排列，此时收集的数据也是对应顺序：

>>> a=tf.range(8)
>>> a=tf.reshape(a,[4,2]) # 生成张量 a
<tf.Tensor: id=115, shape=(4, 2), dtype=int32, numpy=
array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7]])>
>>> tf.gather(a,[3,1,0,2],axis=0) # 收集第 4,2,1,3 号元素
<tf.Tensor: id=119, shape=(4, 2), dtype=int32, numpy=
array([[6, 7],
       [2, 3],
       [0, 1],
       [4, 5]])>

2.tf.gather_nd

通过 tf.gather_nd 函数，可以通过指定每次采样点的多维坐标来实现采样多个点的目的（利用手动一个一个提取然后stack合并的方式也可以达到同样效果，但是效率极低）

参数1：带收集的张量
参数2：指定的采样点的索引坐标

>>> x = tf.random.uniform([4,35,8],maxval=100,dtype=tf.int32) # 成绩册张量（4个班级 35个学生 8门科目）
# 根据多维坐标收集数据
>>> tf.gather_nd(x,[[1,1],[2,2],[3,3]])#抽查第 2 个班级的第 2 个同学的所有科目，第 3 个班级的第 3 个同学的所有科目，第 4 个班级的第 4 个同学的所有科目
<tf.Tensor: id=256, shape=(3, 8), dtype=int32, numpy=
array([[45, 34, 99, 17, 3, 1, 43, 86],
       [11, 25, 84, 95, 97, 95, 69, 69],
       [ 0, 89, 52, 29, 76, 7, 2, 98]])>

一般地，在使用 tf.gather_nd 采样多个样本时，例如希望采样i号班级，j个学生，k门科目的成绩，则可以表达为[. . . , [i,j,k], . . . ]，外层的括号长度为采样样本的个数，内层列表包含了每个采样点的索引坐标

3.tf.boolean_mask

除了可以通过给定索引号的方式采样，还可以通过给定掩码(Mask)的方式进行采样。通过 tf.boolean_mask(x, mask, axis)可以在 axis 轴上根据mask 方案进行采样

>>> x = tf.random.uniform([4,35,8],maxval=100,dtype=tf.int32) # 成绩册张量（4个班级 35个学生 8门科目）
# 根据掩码方式采样班级，给出掩码和维度索引
>>> tf.boolean_mask(x,mask=[True, False,False,True],axis=0)
<tf.Tensor: id=288, shape=(2, 35, 8), dtype=int32, numpy=
array([[[43, 10, 93, 85, 75, 87, 28, 19],...

掩码的长度必须与对应维度的长度一致
掩码可以是List嵌套，此时效果与tf.gather_nd类似

tf.boolean_mask既可以实现了tf.gather方式的一维掩码采样，又可以实现tf.gather_nd方式的多维掩码采样

4.tf.where

通过tf.where(cond, a, b)操作可以根据 cond 条件的真假从参数A或B中读取数据，条件判定规则如下： $o_i=\left\{\begin{matrix} a_i & cond_i为True\\ b_i & cond_i为False \end{matrix}\right.$ 。其中i为张量的元素索引，返回的张量大小与A和B一致，当对应位置的 $cond_i$ 为 True， $o_i$ 从 $a_i$ 中复制数据；当对应位置的 $cond_i$ 为 False， $o_i$ 从 $b_i$ 中复制数据

>>> a = tf.ones([3,3]) # 构造 a 为全 1 矩阵
>>> b = tf.zeros([3,3]) # 构造 b 为全 0 矩阵
# 构造采样条件
>>> cond = tf.constant([[True,False,False],[False,True,False],[True,True,False]])
>>> tf.where(cond,a,b) # 根据条件从 a,b 中采样
<tf.Tensor: id=384, shape=(3, 3), dtype=float32, numpy=
array([[1., 0., 0.],
       [0., 1., 0.],
       [1., 1., 0.]], dtype=float32)>

当参数a=b=None时，tf.where 会返回 cond 张量中所有 True 的元素的索引坐标

>>> cond = tf.constant([[True,False,False],[False,True,False],[True,True,False]])
>>> tf.where(cond) # 获取 cond 中为 True 的元素索引
<tf.Tensor: id=387, shape=(4, 2), dtype=int64, numpy=
array([[0, 0],
       [1, 1],
       [2, 0],
       [2, 1]], dtype=int64)>

例子

>>> x = tf.random.normal([3,3]) # 构造 a
<tf.Tensor: id=403, shape=(3, 3), dtype=float32, numpy=
array([[-2.2946844 , 0.6708417 , -0.5222212 ],
       [-0.6919401 , -1.9418817 , 0.3559235 ],
       [-0.8005251 , 1.0603906 , -0.68819374]], dtype=float32)>
# 通过比较运算，得到所有正数的掩码：
>>> mask=x>0 # 比较操作，等同于 tf.math.greater()
<tf.Tensor: id=405, shape=(3, 3), dtype=bool, numpy=
array([[False, True, False],
       [False, False, True],
       [False, True, False]])>
# 通过 tf.where 提取此掩码处 True 元素的索引坐标：
>>> indices=tf.where(mask) # 提取所有大于 0 的元素索引
<tf.Tensor: id=407, shape=(3, 2), dtype=int64, numpy=
array([[0, 1],
       [1, 2],
       [2, 1]], dtype=int64)>
# 拿到索引后，通过 tf.gather_nd 即可恢复出所有正数的元素：
>>> tf.gather_nd(x,indices) # 提取正数的元素值
<tf.Tensor: id=410, shape=(3,), dtype=float32, numpy=array([0.6708417, 0.3559235, 1.0603906], dtype=float32)>
# 实际上，也可以直接通过 tf.boolean_mask 获取所有正数的元素向量:
>>> tf.boolean_mask(x,mask) # 通过掩码提取正数的元素值
<tf.Tensor: id=439, shape=(3,), dtype=float32, numpy=array([0.6708417, 0.3559235, 1.0603906], dtype=float32)>

5.scatter_nd

通过tf.scatter_nd(indices, updates, shape)函数可以高效地刷新张量的部分数据，但是这个函数只能在全0的白板张量上面执行刷新操作，因此可能需要结合其它操作来实现现有张量的数据刷新功能

白板的形状通过 shape 参数表示，需要刷新的数据索引号通过 indices 表示，新数据为 updates。根据 indices 给出的索引位置将 updates 中新的数据依次写入白板中，并返回更新后的结果张量

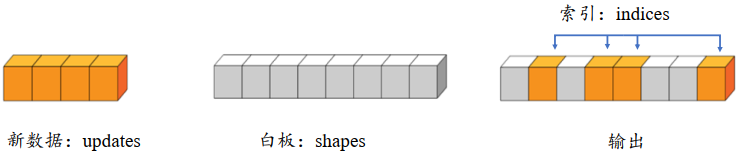
scatter_nd更新数据示意图

# 构造需要刷新数据的位置参数，即为 4、 3、 1 和 7 号位置
>>> indices = tf.constant([[4], [3], [1], [7]])
# 构造需要写入的数据， 4 号位写入 4.4,3 号位写入 3.3，以此类推
>>> updates = tf.constant([4.4, 3.3, 1.1, 7.7])
# 在长度为 8 的全 0 向量上根据 indices 写入 updates 数据
>>> tf.scatter_nd(indices, updates, [8])
<tf.Tensor: id=467, shape=(8,), dtype=float32, numpy=array([0. , 1.1, 0. , 3.3, 4.4, 0. , 0. , 7.7], dtype=float32)>

3维张量刷新例子：

# 构造写入位置，即 2 个位置
>>> indices = tf.constant([[1],[3]])
>>> updates = tf.constant([# 构造写入数据，即 2 个矩阵
[[5,5,5,5],[6,6,6,6],[7,7,7,7],[8,8,8,8]],
[[1,1,1,1],[2,2,2,2],[3,3,3,3],[4,4,4,4]]
])
# 在 shape 为[4,4,4]白板上根据 indices 写入 updates
>>> tf.scatter_nd(indices,updates,[4,4,4])
<tf.Tensor: id=477, shape=(4, 4, 4), dtype=int32, numpy=
array([[[0, 0, 0, 0],
        [0, 0, 0, 0],
        [0, 0, 0, 0],
        [0, 0, 0, 0]],
       [[5, 5, 5, 5], # 写入的新数据 1
        [6, 6, 6, 6],
        [7, 7, 7, 7],
        [8, 8, 8, 8]],
       [[0, 0, 0, 0],
        [0, 0, 0, 0],
        [0, 0, 0, 0],
        [0, 0, 0, 0]],
       [[1, 1, 1, 1], # 写入的新数据 2
        [2, 2, 2, 2],
        [3, 3, 3, 3],
        [4, 4, 4, 4]]])>

6.meshgrid

通过tf.meshgrid函数可以方便地生成二维网格的采样点坐标，方便可视化等应用场合

>>> x = tf.linspace(-8.,8,100) # 设置 x 轴的采样点
>>> y = tf.linspace(-8.,8,100) # 设置 y 轴的采样点
>>> x,y = tf.meshgrid(x,y) # 生成网格点，并内部拆分后返回
>>> x.shape,y.shape # 打印拆分后的所有点的 x,y 坐标张量 shape
(TensorShape([100, 100]), TensorShape([100, 100]))
>>> z = tf.sqrt(x**2+y**2)
>>> z = tf.sin(z)/z # sinc 函数实现
>>> import matplotlib
>>> from matplotlib import pyplot as plt
# 导入 3D 坐标轴支持
>>> from mpl_toolkits.mplot3d import Axes3D
>>> fig = plt.figure()
>>> ax = Axes3D(fig) # 设置 3D 坐标轴
# 根据网格点绘制 sinc 函数 3D 曲面
>>> ax.contour3D(x.numpy(), y.numpy(), z.numpy(), 50)
>>> plt.show()

通过在 x 轴上进行采样 100 个数据点， y 轴上采样 100 个数据点，然后利用tf.meshgrid(x, y)即可返回这 10000 个数据点的张量数据，保存在 shape 为[100,100,2]的张量中。为了方便计算， tf.meshgrid 会返回在 axis=2 维度切割后的 2 个张量A和B，其中张量A包含了所有点的 x 坐标， B包含了所有点的 y 坐标， shape 都为[100,100]

7、经典数据集加载

keras.datasets 模块提供了常用经典数据集的自动下载、管理、加载与转换功能，并且提供了 tf.data.Dataset 数据集对象，方便实现多线程(Multi-threading)、预处理(Preprocessing)、随机打散(Shuffle)和批训练(Training on Batch)等常用数据集的功能

常用的经典数据集：

Boston Housing，波士顿房价趋势数据集，用于回归模型训练与测试
CIFAR10/100，真实图片数据集，用于图片分类任务
MNIST/Fashion_MNIST，手写数字图片数据集，用于图片分类任务
IMDB，情感分类任务数据集，用于文本分类任务

通过datasets.xxx.load_data()函数即可实现经典数据集的自动加载，其中 xxx 代表具体的数据集名称，如“CIFAR10”、“MNIST”。TensorFlow会默认将数据缓存在用户目录下的.keras/datasets 文件夹，用户无需关心数据集是如何保存的。如果当前数据集不在缓存中，则会自动从网络下载、解压和加载数据集；如果已经在缓存中，则自动完成加载

>>> import tensorflow as tf
>>> from tensorflow import keras
>>> from tensorflow.keras import datasets # 导入经典数据集加载模块
# 加载 MNIST 数据集
>>> (x, y), (x_test, y_test) = datasets.mnist.load_data()
>>> print('x:', x.shape, 'y:', y.shape, 'x test:', x_test.shape, 'y test:', y_test)
# 返回数组的形状
x: (60000, 28, 28) y: (60000,) x test: (10000, 28, 28) y test: [7 2 1 ... 4 5 6]

通过 load_data()函数会返回相应格式的数据，对于图片数据集 MNIST、 CIFAR10 等，会返回 2 个 tuple，第一个 tuple 保存了用于训练的数据 x 和 y 训练集对象；第 2 个 tuple 则保存了用于测试的数据 x_test 和 y_test 测试集对象，所有的数据都用 Numpy 数组容器保存

数据加载进入内存后，需要转换成 Dataset 对象。通过Dataset.from_tensor_slices可以将数据转换成Dataset对象

1	>>> train_db = tf.data.Dataset.from_tensor_slices((x, y)) # 以将训练部分的数据图片x和标签y转换成Dataset对象

1.随机打散

通过Dataset.shuffle(buffer_size)工具可以设置 Dataset 对象随机打散数据之间的顺序，防止每次训练时数据按固定顺序产生，从而使得模型尝试“记忆”住标签信息

1 2	# train_db为Dataset对象 >>> train_db = train_db.shuffle(10000) # 随机打散样本，不会打乱样本与标签映射关系

buffer_size 参数指定缓冲池的大小，一般设置为一个较大的常数即可。调用 Dataset提供的这些工具函数会返回新的Dataset对象，可以通过db = db.step1().step2().step3()方式按序完成所有的数据处理步骤

2.批训练

为了利用显卡的并行计算能力，一般在网络的计算过程中会同时计算多个样本，把这种训练方式叫做批训练，其中一个批中样本的数量叫做Batch Size

为了一次能够从Dataset 中产生 Batch Size 数量的样本，需要设置 Dataset 为批训练方式：

1 2	# train_db为Dataset对象 >>> train_db = train_db.batch(128) # 设置批训练， batch size 为 128

一次并行计算 128 个样本的数据

Batch Size 一般根据用户的 GPU 显存资源来设置，当显存不足时，可以适量减少 Batch Size 来减少显存使用量

3.预处理

Dataset 对象通过提供map(func)工具函数，可以非常方便地调用用户自定义的预处理逻辑，它实现在func函数里

def preprocess(x, y): # 自定义的预处理函数
    # 调用此函数时会自动传入 x,y 对象， shape 为[b, 28, 28], [b]
    x = tf.cast(x, dtype=tf.float32) / 255.# 标准化到 0~1
    x = tf.reshape(x, [-1, 28*28]) # 打平
    y = tf.cast(y, dtype=tf.int32) # 转成整型张量
    y = tf.one_hot(y, depth=10) # one-hot 编码
    # 返回的 x,y 将替换传入的 x,y 参数，从而实现数据的预处理功能
    return x,y
# 预处理函数实现在 preprocess 函数中，传入函数名即可
train_db = train_db.map(preprocess)

one_hot：one hot编码会使得y的维度由[b]变为[b, 10]，在后面与网络输出结果out（维度[b, 10]）进行相减然后求计算误差

4.循环训练

对于 Dataset 对象，在使用时可以通过

1	for step, (x,y) in enumerate(train_db): # 迭代数据集对象，带 step 参数

或

1	for x,y in train_db: # 迭代数据集对象

方式进行迭代，每次返回的 x 和 y 对象即为批量样本和标签，当对 train_db 的所有样本完成一次迭代后， for 循环终止退出

这样完成一个 Batch 的数据训练（执行一次循环体），叫做一个Step

通过多个 step 来完成整个训练集的一次迭代（执行一次整个循环），叫做一个Epoch

在实际训练时，通常需要对数据集迭代多个 Epoch 才能取得较好地训练效果：

for epoch in range(20): # 训练 Epoch 数
    for step, (x,y) in enumerate(train_db): # 迭代 Step 数
        # training...
# 可以通过repeat设置epoch的迭代次数（上面与下面等价）
train_db = train_db.repeat(20) # 数据集迭代 20 遍才终止
for step, (x,y) in enumerate(train_db): # 迭代 Step 数
    # training...

通过repeat，使得数据集对象内部遍历多次才会退出

8、MNIST实战

三、神经网络

神经网络属于机器学习的一个研究分支，它特指利用多个神经元去参数化映射函数 $f_\theta$ 的模型

1、感知机

感知机是线性模型，并不能处理线性不可分问题。通过在线性模型后添加激活函数后得到
活性值(Activation) $a$ ： $a=\sigma (z)=\sigma (W^Tx+b)$ ，其中激活函数可以是阶跃函数(Step function)，也可以是符号函数(Sign function)

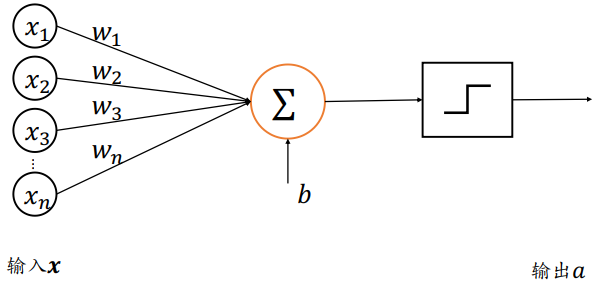
感知机模型

接受长度为𝑛的一维向量 $x=[x_1,x_2,...,x_n]$
每个输入节点通过权值为 $w_i,i\in [1,n]$ $w_{i}, i \in [1, n]$ 的连接汇集为变量𝑧，即： $z=w_1x_1+w_2x_2+...+w_nx_n+b$ $z = w_{1} x_{1} + w_{2} x_{2} + . . . + w_{n} x_{n} + b$
- 𝑏称为感知机的偏置(Bias)
- 一维向量 $W=[w_1,w_2,..w_n]$ 称为感知机的权值(Weight)
- $z$ 称为感知机的净活性值(Net Activation)

但是阶跃函数和符号函数在0处是不连续的，其他位置导数为 0，无法利用梯度下降算法进行参数优化

以感知机为代表的线性模型不能解决异或(XOR)等线性不可分问题

2、全连接层

现代深度学习的核心结构在感知机的基础上，将不连续的阶跃激活函数换成了其它平滑连续可导的激活函数，并通过堆叠多个网络层来增强网络的表达能力

如下所示的整个网络层可以通过矩阵关系式表达 $O=X@W+b$

输入矩阵 $X$ 的 shape 定义为 $[b,d_{in}]$ ， $b$ 为样本数量，此处只有1个样本参与前向运算， $d_{in}$ 为输入节点数（即输入特征长度）
权值矩阵 $W$ 的 shape 定义为 $[d_{in},d_{out}]$ ， $d_{out}$ 为输出节点数（即输出特征长度）
偏置向量 $b$ 的 shape 定义为 $[d_{out}]$
输出矩阵 $O$ 包含了 $b$ 个样本的输出特征， shape 为 $[b,d_{out}]$

由于每个输出节点与全部的输入节点相连接，这种网络层称为全连接层(Fully-connected Layer)，或者稠密连接层(Dense Layer)， $W$ 矩阵叫做全连接层的权值矩阵， $b$ 向量叫做全连接层的偏置向量

全连接层

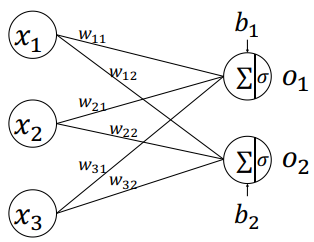
1.张量方式实现

要实现全连接层，只需要定义好权值张量𝑾和偏置张量𝒃，并利用批量矩阵相乘函数tf.matmul()即可完成网络层的计算

例如，创建输入𝑿矩阵为𝑏 = 2个样本，每个样本的输入特征长度为 $d_{in}$ = 784，输出节点数为 $d_{out}$ = 256，故定义权值矩阵𝑾的 shape 为[784,256]，并采用正态分布初始化𝑾；偏置向量𝒃的 shape 定义为[256]，在计算完𝑿@𝑾后相加即可，最终全连接层的输出𝑶的 shape 为[2,256]，即 2 个样本的特征，每个特征长度为 256，代码实现如下：

# 创建 W,b 张量
>>> x = tf.random.normal([2,784])
>>> w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
>>> b1 = tf.Variable(tf.zeros([256]))
>>> o1 = tf.matmul(x,w1) + b1 # 线性变换
>>> o1 = tf.nn.relu(o1) # 激活函数
<tf.Tensor: id=31, shape=(2, 256), dtype=float32, numpy=
array([[ 1.51279330e+00, 2.36286330e+00, 8.16453278e-01,
         1.80338228e+00, 4.58602428e+00, 2.54454136e+00,...

2.层方式实现

作为最常用的网络层之一，TensorFlow中有更高层、使用更方便的层实现方式： layers.Dense(units, activation)。

通过layer.Dense类，只需要指定输出节点数 Units 和激活函数类型 activation 即可

注意：

输入节点数会根据第一次运算时的输入 shape 确定，同时根据输入、输出节点数自动创建并初始化权值张量𝑾和偏置张量𝒃（因此在新建类 Dense 实例时，并不会立即创建权值张量𝑾和偏置张量𝒃，而是需要调用 build 函数或者直接进行一次前向计算，才能完成网络参数的创建）
activation参数指定当前层的激活函数，可以为常见的激活函数或自定义激活函数，也可以指定为 None，即无激活函数

>>> x = tf.random.normal([4,28*28])
>>> from tensorflow.keras import layers # 导入层模块
# 创建全连接层，指定输出节点数和激活函数
>>> fc = layers.Dense(512, activation=tf.nn.relu)
>>> h1 = fc(x) # 通过 fc 类实例完成一次全连接层的计算，返回输出张量
<tf.Tensor: id=72, shape=(4, 512), dtype=float32, numpy=
array([[0.63339347, 0.21663809, 0. , ..., 1.7361937 , 0.39962345, 2.4346168 ],...

通过类内部的成员名 kernel 和 bias 来获取权值张量W和偏置张量b对象：

>>> fc.kernel # 获取 Dense 类的权值矩阵
<tf.Variable 'dense_1/kernel:0' shape=(784, 512) dtype=float32, numpy=
array([[-0.04067389, 0.05240148, 0.03931375, ..., -0.01595572, -0.01075954, -0.06222073],
>>> fc.bias # 获取 Dense 类的偏置向量
<tf.Variable 'dense_1/bias:0' shape=(512,) dtype=float32, numpy=
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,

在优化参数时，需要获得网络的所有待优化的张量参数列表，可以通过类的trainable_variables来返回待优化参数列表

1
2
3

>>> fc.trainable_variables # 返回待优化参数列表
[<tf.Variable 'dense_1/kernel:0' shape=(784, 512) dtype=float32,...,
<tf.Variable 'dense_1/bias:0' shape=(512,) dtype=float32, numpy=...]

网络层除了保存了待优化张量列表 trainable_variables，还有部分层包含了不参与梯度优化的张量，如后续介绍的 Batch Normalization 层，可以通过non_trainable_variables成员返回所有不需要优化参数列表。如果希望获得所有参数列表，可以通过类的variables返回

1
2
3

>>> fc.variables # 返回所有参数列表
[<tf.Variable 'dense_1/kernel:0' shape=(784, 512) dtype=float32,...,
<tf.Variable 'dense_1/bias:0' shape=(512,) dtype=float32, numpy=...]

对于全连接层，内部张量都参与梯度优化

利用网络层类对象进行前向计算时，只需要调用类的__call__方法即可，即写成fc(x)方式便可（会自动调用类的__call__方法，在__call__方法中会自动调用call方法，由 TensorFlow 框架自动完成）

3、神经网络

通过层层堆叠全连接层，保证前一层的输出节点数与当前层的输入节点数匹配，即可堆叠出任意层数的网络。把这种由神经元相互连接而成的网络叫做神经网络

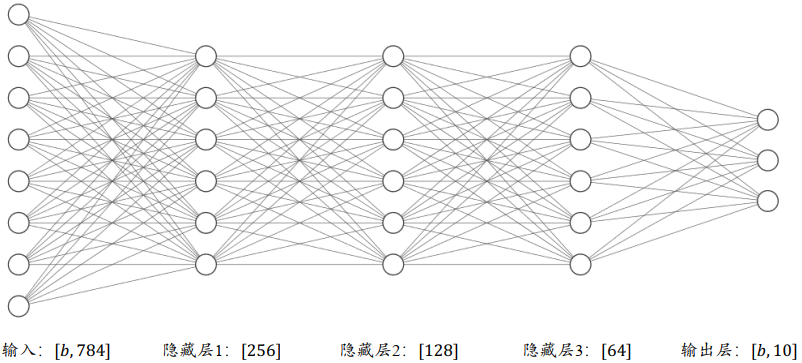
4层神经网络结构

通过堆叠 4 个全连接层，可以获得层数为 4 的神经网络，由于每层均为全连接层，称为全连接网络。其中第 1~3 个全连接层在网络中间，称之为隐藏层1、 2、3，最后一个全连接层的输出作为网络的输出，称为输出层

在设计全连接网络时，网络的结构配置等超参数可以按着经验法则自由设置，只需要遵循少量的约束即可。例如：

隐藏层 1 的输入节点数需和数据的实际特征长度匹配
每层的输入层节点数与上一层输出节点数匹配
输出层的激活函数和节点数需要根据任务的具体设定进行设计。

总的来说，神经网络模型的结构设计自由度较大，至于与哪一组超参数是最优的，这需要很多的领域经验知识和大量的实验尝试

1.张量方式实现

对于多层神经网络，以上图4层网络结构为例，需要分别定义各层的权值矩阵𝑾和偏置向量𝒃，且每层的参数只能用于对应的层，不能混淆使用。在计算时，只需要按照网络层的顺序，将上一层的输出作为当前层的输入即可。最后一层是否需要添加激活函数通常视具体的任务而定

# 隐藏层 1 张量
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
# 隐藏层 2 张量
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))
# 隐藏层 3 张量
w3 = tf.Variable(tf.random.truncated_normal([128, 64], stddev=0.1))
b3 = tf.Variable(tf.zeros([64]))
# 输出层张量
w4 = tf.Variable(tf.random.truncated_normal([64, 10], stddev=0.1))
b4 = tf.Variable(tf.zeros([10]))
with tf.GradientTape() as tape: # 梯度记录器
    # x: [b, 28*28]
    # 隐藏层 1 前向计算， [b, 28*28] => [b, 256]
    h1 = x@w1 + tf.broadcast_to(b1, [x.shape[0], 256])
    h1 = tf.nn.relu(h1)
    # 隐藏层 2 前向计算， [b, 256] => [b, 128]
    h2 = h1@w2 + b2
    h2 = tf.nn.relu(h2)
    # 隐藏层 3 前向计算， [b, 128] => [b, 64]
    h3 = h2@w3 + b3
    h3 = tf.nn.relu(h3)
    # 输出层前向计算， [b, 64] => [b, 10]
    h4 = h3@w4 + b4

在使用 TensorFlow 自动求导功能计算梯度时，需要将前向计算过程放置在tf.GradientTape()环境中，从而利用 GradientTape 对象的 gradient()方法自动求解参数的梯度，并利用 optimizers 对象更新参数

2.层方式实现

# 导入常用网络层 layers
from tensorflow.keras import layers,Sequential
fc1 = layers.Dense(256, activation=tf.nn.relu) # 隐藏层 1
fc2 = layers.Dense(128, activation=tf.nn.relu) # 隐藏层 2
fc3 = layers.Dense(64, activation=tf.nn.relu) # 隐藏层 3
fc4 = layers.Dense(10, activation=None) # 输出层
# 前向计算
x = tf.random.normal([4,28*28])
h1 = fc1(x) # 通过隐藏层 1 得到输出
h2 = fc2(h1) # 通过隐藏层 2 得到输出
h3 = fc3(h2) # 通过隐藏层 3 得到输出
h4 = fc4(h3) # 通过输出层得到网络输出

对于这种数据依次向前传播的网络，也可以通过Sequential容器封装成一个网络大类对象，调用大类的前向计算函数一次即可完成所有层的前向计算

# 导入 Sequential 容器
from tensorflow.keras import layers,Sequential
# 通过 Sequential 容器封装为一个网络类
model = Sequential([
    layers.Dense(256, activation=tf.nn.relu) , # 创建隐藏层 1
    layers.Dense(128, activation=tf.nn.relu) , # 创建隐藏层 2
    layers.Dense(64, activation=tf.nn.relu) , # 创建隐藏层 3
    layers.Dense(10, activation=None) , # 创建输出层
])
# 前向计算得到输出
out = model(x)

3.优化目标

我们把神经网络从输入到输出的计算过程叫做前向传播(Forward Propagation)或前向计算。神经网络的前向传播过程，也是数据张量(Tensor)从第一层流动(Flow)至输出层的过程，即从输入数据开始，途径每个隐藏层，直至得到输出并计算误差，这也是 TensorFlow框架名字由来

前向传播的最后一步就是完成误差的计算 $ℒ=g(𝑓_\theta(x),y)$

其中 $𝑓_\theta(\cdot)$ 代表了利用𝜃参数化的神经网络模型
$g(\cdot)$ 称之为误差函数，用来描述当前网络的预测值 $𝑓_\theta(x)$ 与真实标签𝒚之间的差距度量，比如常用的均方差误差函数
ℒ称为网络的误差(Error，或损失 Loss)，一般为标量

我们希望通过在训练集 $\mathbb{D}^{train}$ 上面学习到一组参数𝜃使得训练的误差ℒ最小：

$\theta^*=\underbrace{arg\ min}_{\theta}g(𝑓_\theta(x),y),x\in \mathbb{D}^{train}$

上述的最小化优化问题一般采用误差反向传播(Backward Propagation，简称 BP)算法来求解网络参数𝜃的梯度信息，并利用梯度下降(Gradient Descent，简称 GD)算法迭代更新参数： $\theta'=\theta-\eta\cdot\bigtriangledown_\thetaℒ$ ，其中𝜂为学习率

网络的参数量是衡量网络规模的重要指标。计算全连接层的参数量方法：

考虑权值矩阵𝑾，偏置向量𝒃，输入特征长度为 $d_{in}$ ，输出特征长度为 $d_{out}$ 的网络层， 𝑾的参数量为 $d_{in}\cdot d_{out}$ ，再加上偏置𝒃的参数，总参数量为 $d_{in}\cdot d_{out}+d_{out}$ 。对于多层的全连接神经网络，总参数量的计算应累加所有全连接层的总参数量

4、激活函数

激活函数都是平滑可导的，适合于梯度下降算法

1.Sigmoid

Sigmoid 函数也叫 Logistic 函数，定义为 $Sigmoid(x)\doteq\frac{1}{1+e^{-x}}$

它的一个优良特性就是能够把𝑥∈𝑅的输入“压缩” 到𝑥∈(0,1)区间，这个区间的数值在机器学习常用来表示以下意义：

概率分布 (0,1)区间的输出和概率的分布范围[0,1]契合，可以通过 Sigmoid 函数将输出转译为概率输出
信号强度：一般可以将 0~1 理解为某种信号的强度（如像素的颜色强度， 1 代表当前通道颜色最强， 0 代表当前通道无颜色；抑或代表门控值(Gate)的强度， 1 代表当前门控全部开放， 0 代表门控关闭）

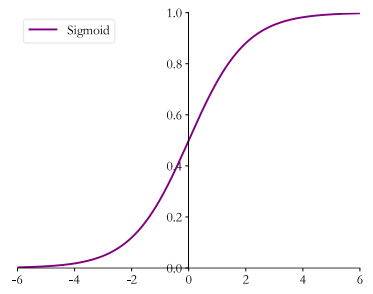
Sigmoid函数曲线

可以通过tf.nn.sigmoid实现 Sigmoid 函数：

>>> x = tf.linspace(-6.,6.,10) # 构造-6~6 的输入向量
>>> tf.nn.sigmoid(x) # 通过 Sigmoid 函数
<tf.Tensor: id=7, shape=(10,), dtype=float32, numpy=
array([0.00247264, 0.00931597, 0.03444517, 0.11920291, 0.33924365, 0.6607564 , 0.8807971 , 0.96555483, 0.99068403, 0.9975274 ], dtype=float32)>

2.ReLU

在 ReLU(REctified Linear Unit，修正线性单元)激活函数提出之前， Sigmoid 函数通常
是神经网络的激活函数首选。

Sigmoid 函数在输入值较大或较小时容易出现梯度值接近于 0 的现象，称为梯度弥散现象。出现梯度弥散现象时，网络参数长时间得不到更新，导致训练不收敛或停滞不动的现象发生，较深层次的网络模型中更容易出现梯度弥散现象

ReLU定义为 $ReLU(x)\doteq max(0,x)$ ，函数曲线如下：

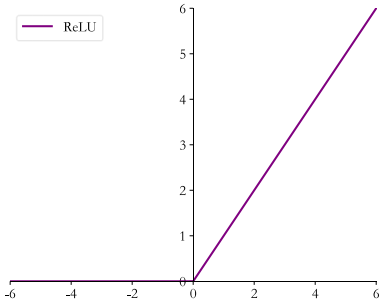
ReLU函数曲线

可以通过tf.nn.relu实现 ReLU 函数：

>>> x = tf.linspace(-6.,6.,10) # 构造-6~6 的输入向量
>>> tf.nn.relu(x) # 通过 ReLU 激活函数
<tf.Tensor: id=11, shape=(10,), dtype=float32, numpy=
array([0. , 0. , 0. , 0. , 0. , 0.666667, 2. , 3.333334, 4.666667, 6. ], dtype=float32)>

除了可以使用函数式接口 tf.nn.relu 实现 ReLU 函数外，还可以像 Dense 层一样将ReLU 函数作为一个网络层添加到网络中，对应的类为 layers.ReLU()类。一般来说，激活
函数类并不是主要的网络运算层，不计入网络的层数

ReLU 函数有着优良的梯度特性，在大量的深度学习应用中被验证非常有效，是应用最广泛的激活函数之一

3.LeakyReLU

ReLU 函数在𝑥 < 0时导数值恒为 0，也可能会造成梯度弥散现象，为了克服这个问
题， LeakyReLU 函数被提出： $LeakyReLU\doteq \left\{\begin{matrix} x & x\geqslant 0\\ px & x<0 \end{matrix}\right.$

其中𝑝为用户自行设置的某较小数值的超参数，如 0.02 等。当𝑝 = 0时， LeayReLU 函数退化为 ReLU 函数；当𝑝 ≠ 0时， 𝑥 < 0处能够获得较小的导数值𝑝，从而避免出现梯度弥散现象

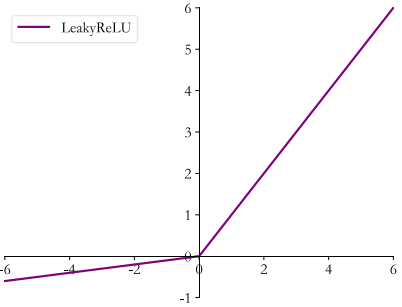
LeakyReLU函数曲线

可以通过tf.nn.leaky_relu实现 LeakyReLU 函数：

>>> x = tf.linspace(-6.,6.,10) # 构造-6~6 的输入向量
>>> tf.nn.leaky_relu(x, alpha=0.1) # 通过 LeakyReLU 激活函数
<tf.Tensor: id=13, shape=(10,), dtype=float32, numpy=
array([-0.6 , -0.46666667, -0.33333334, -0.2 , -0.06666666, 0.666667 , 2. , 3.333334 , 4.666667 , 6. ], dtype=float32)>

alpha 参数代表𝑝

tf.nn.leaky_relu 对应的类为 layers.LeakyReLU，可以通过LeakyReLU(alpha)创建LeakyReLU 网络层，并设置𝑝参数，像 Dense 层一样将 LeakyReLU层放置在网络的合适位置

4.Tanh

Tanh 函数能够将𝑥 ∈ 𝑅的输入“压缩” 到(-1,1)区间，定义为： $tanh(x)\doteq\frac{e^x-e^{-x}}{e^x+e^{-x}}=2sigmoid(2x)-1$ （tanh 激活函数可通过 Sigmoid 函数缩放平移后实现）

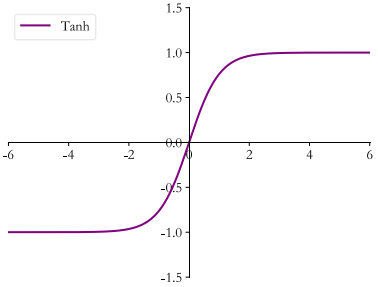
tanh函数曲线

可以通过 tf.nn.tanh 实现 tanh 函数：

>>> x = tf.linspace(-6.,6.,10) # 构造-6~6 的输入向量
>>> tf.nn.tanh(x) # 通过 tanh 激活函数
<tf.Tensor: id=15, shape=(10,), dtype=float32, numpy=
array([-0.9999877 , -0.99982315, -0.997458 , -0.9640276 , -0.58278286, 0.5827831 , 0.9640276 , 0.997458 , 0.99982315, 0.9999877 ], dtype=float32)>

5、输出层设计

常见的几种输出类型包括：

𝑜𝑖 ∈ $𝑅^𝑑$ 输出属于整个实数空间，或者某段普通的实数空间，比如函数值趋势的预测，年龄的预测问题等
𝑜𝑖 ∈ [0,1] 输出值特别地落在[0, 1]的区间，如图片生成，图片像素值一般用[0, 1]区间的值表示；或者二分类问题的概率，如硬币正反面的概率预测问题
𝑜𝑖 ∈ [0, 1], 𝑖 𝑜𝑖 = 1 输出值落在[0, 1]的区间，并且所有输出值之和为 1，常见的如多分类问题，如 MNIST 手写数字图片识别，图片属于 10 个类别的概率之和应为 1
𝑜𝑖 ∈ [-1, 1] 输出值在[-1, 1]之间

1.普通实数空间

该类问题较普遍，输出层可以不加激活函数。

误差的计算直接基于最后一层的输出𝒐和真实值𝒚进行计算，如采用均方差误差函数度量输出值𝒐与真实值𝒚之间的距离：ℒ = 𝑔(𝒐, 𝒚)，其中𝑔代表了某个具体的误差计算函数，例如 MSE 等

2.[0,1]区间

为了让像素的值范围映射到[0,1]的有效实数空间，需要在输出层后添加某个合适的激活函数𝜎，其中 Sigmoid 函数刚好具有此功能

对于二分类问题，如硬币的正反面的预测，输出层可以只设置一个节点，表示某个事件 A 发生的概率𝑃(A|𝒙)， 𝒙为网络输入。假设网络的输出标量𝑜表示正面事件出现的概率，则反面事件出现的概率即为1 - 𝑜，网络结构如下所示

𝑃(正面|𝒙) = 𝑜
𝑃(反面|𝒙) = 1 - 𝑜

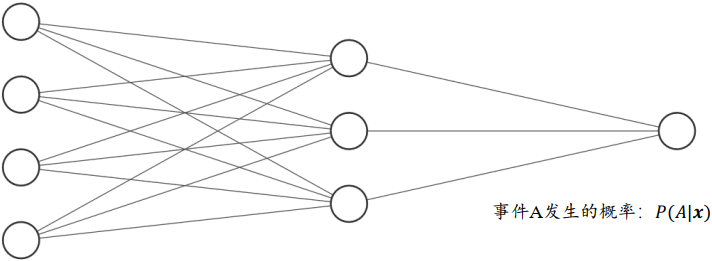
单输出节点的二分类网络

输出层的净活性值𝑧后添加 Sigmoid 函数即可将输出转译为概率值

3.[0,1]区间，和为1

输出值𝑜𝑖 ∈ [0,1]，且所有输出值之和为 1，这种设定以多分类问题最为常见

可以通过在输出层添加 Softmax 函数实现： $Softmax(z_i)=\frac{e^{Z_i}}{\sum^{d_{out}}_{j=1}e^{Z_j}}$

Softmax 函数不仅可以将输出值映射到[0,1]区间，还满足所有的输出值之和为 1 的特性
通过 Softmax函数可以将输出层的输出转译为类别概率，在分类问题中使用的非常频繁

可以通过 tf.nn.softmax 实现 Softmax 函数：

1
2
3

>>> z = tf.constant([2.,1.,0.1])
>>> tf.nn.softmax(z) # 通过 Softmax 函数
<tf.Tensor: id=19, shape=(3,), dtype=float32, numpy=array([0.6590012, 0.242433 , 0.0985659], dtype=float32)>

与 Dense 层类似， Softmax 函数也可以作为网络层类使用，通过类layers.Softmax(axis=-1)可以方便添加 Softmax 层，其中 axis 参数指定需要进行计算的维度

在 Softmax 函数的数值计算过程中，容易因输入值偏大发生数值溢出现象；在计算交叉熵时，也会出现数值溢出的问题。为了数值计算的稳定性， TensorFlow 中提供了一个统一的接口，将 Softmax 与交叉熵损失函数同时实现，同时也处理了数值不稳定的异常，一般推荐使用这些接口函数，避免分开使用 Softmax 函数与交叉熵损失函数。函数式接口为tf.keras.losses.categorical_crossentropy(y_true, y_pred, from_logits=False)

y_true：One-hot 编码后的真实标签
y_pred：网络的预测值
- 当 from_logits 设置为 True 时，y_pred 表示须为未经过 Softmax 函数的变量 z
- 当 from_logits 设置为 False 时， y_pred 表示为经过 Softmax 函数的输出
为了数值计算稳定性，一般设置 from_logits 为 True（此时tf.keras.losses.categorical_crossentropy将在内部进行 Softmax 函数计算，所以不需要在模型中显式调用 Softmax 函数）

>>> z = tf.random.normal([2,10]) # 构造输出层的输出
>>> y_onehot = tf.constant([1,3]) # 构造真实值
>>> y_onehot = tf.one_hot(y_onehot, depth=10) # one-hot 编码
# 输出层未使用 Softmax 函数，故 from_logits 设置为 True
# 这样 categorical_crossentropy 函数在计算损失函数前，会先内部调用 Softmax 函数
>>> loss = keras.losses.categorical_crossentropy(y_onehot,z,from_logits=True)
>>> loss = tf.reduce_mean(loss) # 计算平均交叉熵损失
<tf.Tensor: id=210, shape=(), dtype=float32, numpy= 2.4201946>

除了函数式接口，也可以利用losses.CategoricalCrossentropy(from_logits)类方式同时实现 Softmax 与交叉熵损失函数的计算， from_logits 参数的设置方式相同

# 创建 Softmax 与交叉熵计算类，输出层的输出 z 未使用 softmax
>>> criteon = keras.losses.CategoricalCrossentropy(from_logits=True)
>>> loss = criteon(y_onehot,z) # 计算损失
<tf.Tensor: id=258, shape=(), dtype=float32, numpy= 2.4201946>

4.[-1,1]区间

使用 tanh 激活函数即可：

>>> x = tf.linspace(-6.,6.,10)
>>> tf.tanh(x) # tanh 激活函数
<tf.Tensor: id=264, shape=(10,), dtype=float32, numpy=
array([-0.9999877 , -0.99982315, -0.997458 , -0.9640276 , -0.58278286, 0.5827831 , 0.9640276 , 0.997458 , 0.99982315, 0.9999877 ], dtype=float32)>

6、误差计算

常见的误差函数有均方差、交叉熵、 KL 散度、 Hinge Loss 函数等，其中均方差函数和交叉熵函数在深度学习中比较常见，均方差函数主要用于回归问题，交叉熵函数主要用于分类问题

1.均方差误差函数

均方差(Mean Squared Error，简称 MSE)误差函数：把输出向量和真实向量映射到笛卡尔坐标系的两个点上，通过计算这两个点之间的欧式距离(准确地说是欧式距离的平方)来衡量两个向量之间的差距：

$MSE(y,o)=\frac{1}{d_{out}}\sum^{d_{out}}_{i=1}(y_i-o_i)^2$

MSE 误差函数的值总是大于等于 0
当 MSE 函数达到最小值 0 时，输出等于真实标签，此时神经网络的参数达到最优状态

可以通过函数方式或层方式实现 MSE 误差计算。通过函数式调用：

>>> o = tf.random.normal([2,10]) # 构造网络输出
>>> y_onehot = tf.constant([1,3]) # 构造真实值
>>> y_onehot = tf.one_hot(y_onehot, depth=10)
>>> loss = keras.losses.MSE(y_onehot, o) # 计算均方差
<tf.Tensor: id=27, shape=(2,), dtype=float32, numpy=array([0.779179 ,
1.6585705], dtype=float32)>

MSE 函数返回的是每个样本的均方差

可以在样本维度上再次平均来获得平均样本的均方差

1 2	>>> loss = tf.reduce_mean(loss) # 计算 batch 均方差 <tf.Tensor: id=30, shape=(), dtype=float32, numpy=1.2188747>

通过层方式实现，对应的类为keras.losses.MeanSquaredError()，和其他层的类一样，调用__call__函数即可完成前向计算：

# 创建 MSE 类
>>> criteon = keras.losses.MeanSquaredError()
>>> loss = criteon(y_onehot,o) # 计算 batch 均方差
<tf.Tensor: id=54, shape=(), dtype=float32, numpy=1.2188747>

2.交叉熵误差函数

熵，在信息论中，用来衡量信息的不确定度。熵在信息学科中也叫信息熵，或者香农熵。熵越大，代表不确定性越大，信息量也就越大。某个分布𝑃(𝑖)的熵定义为： $H(P)=-\sum_iP(i)log_2P(i)$

对于确定的分布，熵取得最小值0，不确定性为0
由于𝑃(𝑖) ∈ [0,1], $log_2P(i)$ ≤ 0，因此熵𝐻(𝑃)总是大于等于 0
在 TensorFlow 中，可以用tf.math.log来计算熵

交叉熵(Cross Entropy)的定义： $H(p||q)=H(p)+D_{KL}(p||q)$

其中 $D_{KL}(p||q)$ $D_{K L} (p ∣ ∣ q)$ 为𝑝与𝑞的 KL 散度(Kullback-Leibler Divergence)： $D_{KL}(p||q)=\sum_ip(i)log(\frac{p(i)}{q(i)})$ $D_{K L} (p ∣ ∣ q) = \sum_{i} p (i) l o g (\frac{p ( i )}{q ( i )})$
- KL 散度是用于衡量 2 个分布之间距离的指标：𝑝 = 𝑞时， $D_{KL}(p||q)$ 取得最小值 0， 𝑝与𝑞之间的差距越大， $D_{KL}(p||q)$ 也越大
- 交叉熵和 KL 散度都不是对称的：
  - $H(p||q)\neq H(q||p)$
  - $D_{KL}(p||q)\neq D_{KL}(q||p)$
当分类问题中 y 的编码分布𝑝采用 One-hot 编码𝒚时： 𝐻(𝑝) = 0

分类问题中交叉熵的计算表达式： $H(p||q)=D_{KL}(p||q)=-logo_i$

𝑖为 One-hot 编码中为 1 的索引号，也是当前输入的真实类别
ℒ只与真实类别𝑖上的概率𝑜𝑖有关，对应概率𝑜𝑖越大， 𝐻(𝑝||𝑞)越小
当对应类别上的概率为 1 时，交叉熵𝐻(𝑝||𝑞)取得最小值 0，此时网络输出𝒐与真实标签𝒚完全一致，神经网络取得最优状态
最小化交叉熵损失函数的过程也是最大化正确类别的预测概率的过程

7、神经网络类型

全连接层是神经网络最基本的网络类型，优点是全连接层前向计算流程相对简单，梯度求导也较简单，缺点是在处理较大特征长度的数据时，全连接层的参数量往往较大

1.卷积神经网络

全连接层在处理高维度的图片、视频数据时往往出现网络参数量巨大，训练非常困难。通过利用局部相关性和权值共享的思想，Yann Lecun在1986年提出了卷积神经网络(Convolutional Neural Network，简称 CNN)

其中比较流行的模型：

用于图片分类的 AlexNet、 VGG、 GoogLeNet、 ResNet、 DenseNet 等
用于目标识别的 RCNN、 Fast RCNN、 Faster RCNN、 Mask RCNN、 YOLO、 SSD 等

2.循环神经网络

除了具有空间结构的图片、视频等数据外，序列信号也是非常常见的一种数据类型，其中一个最具代表性的序列信号就是文本数据。卷积神经网络由于缺乏 Memory 机制和处理不定长序列信号的能力，并不擅长序列信号的任务。循环神经网络(Recurrent Neural Network)，被证明非常擅长处理序列信号

1997年提出的LSTM网络，作为 RNN 的变种，较好地克服了 RNN 缺乏长期记忆、不擅长处理长序列的问题，在自然语言处理中得到了广泛的应用。基于LSTM 模型， Google 提出了用于机器翻译的 Seq2Seq 模型，并成功商用于谷歌神经机器翻译系统(GNMT)

其他的 RNN 变种还有 GRU、双向 RNN 等

3.注意力（机制）网络

RNN 并不是自然语言处理的最终解决方案，近年来随着注意力机制(Attention Mechanism)的提出，克服了 RNN 训练不稳定、难以并行化等缺陷，在自然语言处理和图片生成等领域中逐渐崭露头角

2017 年， Google 提出了第一个利用纯注意力机制实现的网络模型Transformer，随后基于 Transformer 模型相继提出了一系列的用于机器翻译的注意力网络模型，如 GPT、 BERT、 GPT-2 等

在其它领域，基于注意力机制，尤其是自注意力(SelfAttention)机制构建的网络也取得了不错的效果，比如基于自注意力机制的 BigGAN 模型等

4.图卷积神经网络

图片、文本等数据具有规则的空间、时间结构，称为 Euclidean Data(欧几里德数据)。卷积神经网络和循环神经网络被证明非常擅长处理这种类型的数据。而像类似于社交网络、通信网络、蛋白质分子结构等一系列的不规则空间拓扑结构的数据，它们显得力不从心。 2016 年，基于前人在一阶近似的谱卷积算法上提出了图卷积网络(Graph Convolution Network， GCN)模型。 GCN 算法实现简单，从空间一阶邻居信息聚合的角度也能直观地理解，在半监督任务上取得了不错效果。随后，一系列的网络模型相继被提出，如 GAT， EdgeConv， DeepGCN 等

四、Keras高层接口

Keras 与 tf.keras 的区别与联系：

Keras 可以理解为一套搭建与训练神经网络的高层 API 协议， Keras 本身已经实现了此协议，安装标准的 Keras 库就可以方便地调用TensorFlow、 CNTK 等后端完成加速计算
在 TensorFlow 中，也实现了一套 Keras 协议，即 tf.keras，它与 TensorFlow 深度融合，且只能基于 TensorFlow 后端运算，并对TensorFlow 的支持更完美。对于使用 TensorFlow 的开发者来说， tf.keras 可以理解为一个普通的子模块，与其他子模块，如 tf.math， tf.data 等并没有什么差别。下文如无特别说明，Keras 均指代 tf.keras，而不是标准的 Keras 库

1、常见功能模块

Keras 提供了一系列高层的神经网络相关类和函数，如经典数据集加载函数（进阶操作–>经典数据集加载章节中讲到过）、网络层类、模型容器、损失函数类、优化器类、经典模型类等

1.常见网络层类

对于常见的神经网络层，可以使用张量方式的底层接口函数来实现，这些接口函数一般在tf.nn模块中。

对于常见的网络层，我们一般直接使用层方式来完成模型的搭建，在tf.keras.layers命名空间(下文使用 layers 指代 tf.keras.layers)中提供了大量常见网络层的类，如全连接层、激活函数层、池化层、卷积层、循环神经网络层等。对于这些网络层类，只需要在创建时指定网络层的相关参数，并调用__call__方法即可完成前向计算。在调用__call__方法时， Keras 会自动调用每个层的前向传播逻辑，这些逻辑一般实现在类的call 函数中。

以 Softmax 层为例，它既可以使用tf.nn.softmax函数在前向传播逻辑中完成Softmax运算，也可以通过layers.Softmax(axis)类搭建Softmax网络层，其中axis参数指定进行softmax 运算的维度：

>>> import tensorflow as tf
# 导入 keras 模型，不能使用 import keras，它导入的是标准的 Keras 库
>>> from tensorflow import keras
>>> from tensorflow.keras import layers # 导入常见网络层类
# 创建 Softmax 层，并调用__call__方法完成前向计算
>>> x = tf.constant([2.,1.,0.1]) # 创建输入张量
>>> layer = layers.Softmax(axis=-1) # 创建 Softmax 层
>>> out = layer(x) # 调用 softmax 前向计算，输出为 out
# 经过 Softmax 网络层后， 得到概率分布 out 为：
<tf.Tensor: id=2, shape=(3,), dtype=float32, numpy=array([0.6590012, 0.242433 , 0.0985659], dtype=float32)>
# 当然，也可以直接通过 tf.nn.softmax()函数完成计算，代码如下：
>>> out = tf.nn.softmax(x) # 调用 softmax 函数完成前向计算

2.网络容器

当网络层数变得较深时，手动调用每一层的类实例完成前向传播运算这部分代码显得非常臃肿。可以通过 Keras 提供的网络容器 Sequential 将多个网络层封装成一个大网络模型，只需要调用网络模型的实例一次即可完成数据从第一层到最末层的顺序传播运算

# 导入 Sequential 容器
from tensorflow.keras import layers, Sequential
network = Sequential([ # 封装为一个网络
    layers.Dense(3, activation=None), # 全连接层，此处不使用激活函数
    layers.ReLU(),#激活函数层
    layers.Dense(2, activation=None), # 全连接层，此处不使用激活函数
    layers.ReLU() #激活函数层
])
x = tf.random.normal([4,3])
out = network(x) # 输入从第一层开始， 逐层传播至输出层，并返回输出层的输出

Sequential 容器也可以通过add()方法继续追加新的网络层，实现动态创建网络的功能：

layers_num = 2 # 堆叠 2 次
network = Sequential([]) # 先创建空的网络容器
for _ in range(layers_num):
    network.add(layers.Dense(3)) # 添加全连接层
    network.add(layers.ReLU())# 添加激活函数层
network.build(input_shape=(4, 4)) # 创建网络参数
network.summary()

在完成网络创建时，网络层类并没有创建内部权值张量等成员变量，此时通过调用类的build方法并指定输入大小，即可自动创建所有层的内部张量
通过Sequential容量封装多个网络层时，每层的参数列表将会自动并入Sequential容器的参数列表中，不需要人为合并网络参数列表

Sequential 对象的trainable_variables和variables包含了所有层的待优化张量列表和全部张量列表

# 打印网络的待优化参数名与 shape
>>> for p in network.trainable_variables:
...     print(p.name, p.shape) # 参数名和形状
...
dense/kernel:0 (4, 3)
dense/bias:0 (3,)
dense_1/kernel:0 (3, 3)
dense_1/bias:0 (3,)

通过summary()函数可以方便打印出网络结构和参数量，输出：

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
dense (Dense)                multiple                  15
_________________________________________________________________
re_lu (ReLU)                 multiple                  0
_________________________________________________________________
dense_1 (Dense)              multiple                  12
_________________________________________________________________
re_lu_1 (ReLU)               multiple                  0
=================================================================
Total params: 27
Trainable params: 27
Non-trainable params: 0
_________________________________________________________________

Layer：每层的名字，由 TensorFlow 内部维护，与 Python 的对象名并不一样
Param#：层的参数个数
Total params：统计出了总的参数量
Trainable params：总的待优化参数量
Non-trainable params：总的不需要优化的参数量

2、模型装配、训练与测试

在训练网络时，一般的流程是通过前向计算获得网络的输出值，再通过损失函数计算网络误差，然后通过自动求导工具计算梯度并更新，同时间隔性地测试网络的性能。对于这种常用的训练逻辑，可以直接通过 Keras 提供的模型装配与训练等高层接口实现

1.模型装配

在 Keras 中，有 2 个比较特殊的类：

keras.Model类：网络的母类，除了具有Layer类的功能，还添加了保存模型、加载模型、训练与测试模型等便捷功能。Sequential也是Model的子类（具有Model类的所有功能）
keras.layers.Layer类：网络层的母类，定义了网络层的一些常见功能，如添加权值、管理权值列表等

下面介绍 Model 及其子类的模型装配与训练功能

创建网络：

# 创建 5 层的全连接网络
network = Sequential([layers.Dense(256, activation='relu'),
                      layers.Dense(128, activation='relu'),
                      layers.Dense(64, activation='relu'),
                      layers.Dense(32, activation='relu'),
                      layers.Dense(10)])
network.build(input_shape=(4, 28*28))  # 构建网络（此时网络中的权重w与偏差b才会生成）
network.summary()  # 打印出网络结构和参数量

通过compile函数指定网络使用的优化器对象、损失函数类型，评价指标等设定，这一步称为装配

# 导入优化器，损失函数模块
from tensorflow.keras import optimizers,losses
# 模型装配
# 采用 Adam 优化器，学习率为 0.01;采用交叉熵损失函数，包含 Softmax
network.compile(optimizer=optimizers.Adam(lr=0.01),
                loss=losses.CategoricalCrossentropy(from_logits=True),
                metrics=['accuracy'] # 设置测量指标为准确率
               )

2.模型训练

模型装配完成后，可通过fit()函数送入待训练的数据集和验证用的数据集，实现网络的训练与验证，这一步称为模型训练

# 指定训练集为 train_db，验证集为 val_db,训练 5 个 epochs，每 2 个 epoch 验证一次
# 返回训练轨迹信息保存在 history 对象中
history = network.fit(train_db, epochs=5, validation_data=val_db,
                      validation_freq=2)

train_db：tf.data.Dataset对象，也可以传入Numpy Array类型的数据
epochs：指定训练迭代的Epoch数量
validation_data：指定用于验证(测试)的数据集
validation_freq：验证的频率

history：训练过程的数据记录，其中history.history为字典对象，包含了训练过程中的loss、测量指标等记录项

>>> history.history # 打印训练记录
# 历史训练准确率
{'accuracy': [0.00011666667, 0.0, 0.0, 0.010666667, 0.02495],
 'loss': [2465719710540.5845, # 历史训练误差
          78167808898516.03,
          404488834518159.6,
          1049151145155144.4,
          1969370184858451.0],
 'val_accuracy': [0.0, 0.0], # 历史验证准确率
 # 历史验证误差
 'val_loss': [197178788071657.3, 1506234836955706.2]}

fit()函数的运行代表了网络的训练过程，会消耗相当的训练时间，并在训练结束后才返回

3.模型测试

关于验证和测试的区别，会在过拟合一章详细阐述，此处可以将验证和测试理解为模型评估的一种方式

通过Model.predict(x)方法即可完成模型的预测：

# 加载一个 batch 的测试数据
x,y = next(iter(db_test))
print('predict x:', x.shape) # 打印当前 batch 的形状
out = network.predict(x) # 模型预测，预测结果保存在 out 中
print(out)

如果只是简单的测试模型的性能，可以通过Model.evaluate(db)循环测试完db数据集上所有样本，并打印出性能指标：

1	network.evaluate(db_test) # 模型测试，测试在 db_test 上的性能表现

3、模型保存与加载

1.张量方式

网络的状态主要体现在网络的结构以及网络层内部张量数据上，因此在拥有网络结构源文件的条件下，直接保存网络张量参数到文件系统上是最轻量级的一种方式

通过调用Model.save_weights(path)方法，可将当前的网络参数保存到path文件上

1	network.save_weights('weights.ckpt') # 保存模型的所有张量数据

在需要的时候，先创建好网络对象，然后调用网络对象的load_weights(path)方法即可将指定的模型文件中保存的张量数值写入到当前网络参数中

# 重新创建相同的网络结构
new_network = Sequential([layers.Dense(256, activation='relu'),
                          layers.Dense(128, activation='relu'),
                          layers.Dense(64, activation='relu'),
                          layers.Dense(32, activation='relu'),
                          layers.Dense(10)])
new_network.compile(optimizer=optimizers.Adam(lr=0.01),
                    loss=tf.losses.CategoricalCrossentropy(from_logits=True),
                    metrics=['accuracy']
                   )
# 从参数文件中读取数据并写入当前网络
new_network.load_weights('weights.ckpt')
print('loaded weights!')

2.网络方式

通过Model.save(path)函数可以将模型的结构以及模型的参数保存到path文件上，在不需要网络源文件的条件下，通过keras.models.load_model(path)即可恢复网络结构和网络参数

# 保存模型结构与模型参数到文件
network.save('model.h5')
print('saved total model.')
del network # 删除网络对象
# 从文件恢复网络结构与网络参数
network = keras.models.load_model('model.h5')

3.SavedModel方式

当需要将模型部署到其他平台时，采用SavedModel方式更具有平台无关性。

通过tf.saved_model.save(network, path)即可将模型以SavedModel方式保存到path目录中

# 保存模型结构与模型参数到文件
tf.saved_model.save(network, 'model-savedmodel')
print('saving savedmodel.')
del network # 删除网络对象

通过tf.saved_model.load函数即可恢复出模型对象，我们在恢复出模型实例后，完成测试准确率的计算

# 从文件恢复网络结构与网络参数
network = tf.saved_model.load('model-savedmodel')
# 准确率计量器
acc_meter = metrics.CategoricalAccuracy()
for x,y in ds_val: # 遍历测试集
    pred = network(x) # 前向计算
    acc_meter.update_state(y_true=y, y_pred=pred) # 更新准确率统计
# 打印准确率
print("Test Accuracy:%f" % acc_meter.result())

4、自定义网络

对于需要创建自定义逻辑的网络层，可以通过自定义类来实现

在创建自定义网络层类时，需要继承自 layers.Layer 基类
创建自定义的网络类时，需要继承自 keras.Model 基类

1.自定义网络层

对于自定义的网络层，需要实现初始化__init__方法和前向传播逻辑call方法

以某个具体的自定义网络层为例，假设需要一个没有偏置向量的全连接层，同时固定激活函数为 ReLU 函数：

首先创建类，并继承自 Layer 基类。创建初始化方法，并调用母类的初始化函数。由于是全连接层，因此需要设置两个参数：输入特征的长度inp_dim和输出特征的长度outp_dim，并通过self.add_variable(name, shape)创建 shape 大小，名字为 name 的张量𝑾，并设置为需要优化

class MyDense(layers.Layer):
    # 自定义网络层
    def __init__(self, inp_dim, outp_dim):
        super(MyDense, self).__init__() # 调用母类的初始化函数
        # 创建权值张量并添加到类管理列表中，设置为需要优化
        self.kernel = self.add_variable('w', [inp_dim, outp_dim],
                                        trainable=True)
        # 此外，通过 tf.Variable 创建的类成员也会自动加入类参数列表
        # self.kernel = tf.Variable(tf.random.normal([inp_dim, outp_dim]),
        #                           trainable=False)

self.add_variable会返回张量𝑾的 Python 引用
变量名 name 由TensorFlow 内部维护，使用的比较少
trainable：创建的张量是否需要优化

设计自定义类的前向运算逻辑。对于本例，只需要完成𝑶 = 𝑿@𝑾矩阵运算，并通过固定的ReLU激活函数即可
1
2
3
4
5
6
7
def call(self, inputs, training=None):
# 实现自定义类的前向计算逻辑
# X@W
out = inputs @ self.kernel
# 执行激活函数运算
out = tf.nn.relu(out)
return out
- inputs：输入，由用户在调用时传入
- training：用于指定模型的状态：
  - True：执行训练模式
  - False：执行测试模式，默认参数为 None，即测试模式
- 由于全连接层的训练模式和测试模式逻辑一致，此处不需要额外处理。对于部份测试模式和训练模式不一致的网络层，需要根据 training 参数来设计需要执行的逻辑

此时可以实例化 MyDense 类，并查看其参数列表：

1 2	net = MyDense(4,3) # 创建输入为 4，输出为 3 节点的自定义层 net.variables,net.trainable_variables # 查看自定义层的参数列表

2.自定义网络

自定义网络类可以和其他标准类一样，通过 Sequential 容器方便地封装成一个网络模型：

network = Sequential([MyDense(784, 256), # 使用自定义的层
                      MyDense(256, 128),
                      MyDense(128, 64),
                      MyDense(64, 32),
                      MyDense(32, 10)])
network.build(input_shape=(None, 28*28))
network.summary()

通过堆叠自定义网络层类，可以实现 5 层的全连接层网络，每层全连接层无偏置张量，同时激活函数固定地使用 ReLU 函数

Sequential 容器适合于数据按序从第一层传播到第二层，再从第二层传播到第三层，以此规律传播的网络模型。对于复杂的网络结构，例如第三层的输入不仅是第二层的输出，还有第一层的输出，此时使用自定义网络更加灵活：

创建自定义网络类，首先创建类，并继承自 Model 基类，分别创建对应的网络层对象：

class MyModel(keras.Model):
    # 自定义网络类，继承自 Model 基类
    def __init__(self):
        super(MyModel, self).__init__() # 调用母类的初始化函数
        # 完成网络内需要的网络层的创建工作
        self.fc1 = MyDense(28*28, 256)
        self.fc2 = MyDense(256, 128)
        self.fc3 = MyDense(128, 64)
        self.fc4 = MyDense(64, 32)
        self.fc5 = MyDense(32, 10)

实现自定义网络的前向运算逻辑：

def call(self, inputs, training=None):
    # 自定义前向运算逻辑
    x = self.fc1(inputs)
    x = self.fc2(x)
    x = self.fc3(x)
    x = self.fc4(x)
    x = self.fc5(x)
    return x

5、模型乐园

对于常用的网络模型，如 ResNet、 VGG 等，不需要手动创建网络，可以直接从keras.applications子模块中通过一行代码即可创建并使用这些经典模型，同时还可以通过设置 weights 参数加载预训练的网络参数

1.加载模型

暂无，等待施工

6、测量工具

Keras 提供了一些常用的测量工具，位于keras.metrics模块中，专门用于统计训练过程中常用的指标数据。Keras 的测量工具的使用方法一般有 4 个主要步骤：

新建测量器
写入数据
读取统计数据
清零测量器

1.新建测量器

在keras.metrics模块中，提供了较多的常用测量器类，如统计平均值的 Mean 类，统计准确率的 Accuracy 类，统计余弦相似度的 CosineSimilarity 类等

例子：统计误差值

在前向运算时，会得到每一个 Batch 的平均误差，但是希望统计每个Step的平均误差，因此选择使用Mean测量器：

1 2	# 新建平均测量器，适合 Loss 数据 loss_meter = metrics.Mean()

2.写入数据

通过测量器的update_state函数可以写入新的数据，测量器会根据自身逻辑记录并处理采样数据。例如，在每个 Step 结束时采集一次 loss 值，代码如下：

1 2	# 记录采样的数据，通过 float()函数将张量转换为普通数值 loss_meter.update_state(float(loss))

放置在每个 Batch 运算结束后即可，测量器会自动根据采样的数据来统计平均值

3.读取统计信息

在采样多次数据后，可以选择在需要的地方调用测量器的result()函数，来获取统计值

1 2	# 打印统计期间的平均 loss print(step, 'loss:', loss_meter.result())

4.清除状态

测量器会统计所有历史记录的数据，因此在启动新一轮统计时，有必要清除历史状态。通过 reset_states() 即可实现清除状态功能

例如，在每次读取完平均误差后，清零统计信息，以便下一轮统计的开始

if step % 100 == 0:
    # 打印统计的平均 loss
    print(step, 'loss:', loss_meter.result())
    loss_meter.reset_states() # 打印完后， 清零测量器

5.准确率统计实战

新建准确率测量器

1	acc_meter = metrics.Accuracy() # 创建准确率测量器

Accuracy 类的 update_state 函数的参数为预测值和真实值，而不是当前 Batch 的准确率

# [b, 784] => [b, 10]，网络输出值
out = network(x)
# [b, 10] => [b]，经过 argmax 后计算预测值
pred = tf.argmax(out, axis=1)
pred = tf.cast(pred, dtype=tf.int32)
# 根据预测值与真实值写入测量器
acc_meter.update_state(y, pred)

在统计完测试集所有 Batch 的预测值后，打印统计的平均准确率，并清零测量器

1
2
3

# 读取统计结果
print(step, 'Evaluate Acc:', acc_meter.result().numpy())
acc_meter.reset_states() # 清零测量器

7、可视化

TensorFlow 提供了一个可视化工具TensorBoard。原理是通过将监控数据写入到文件系统，并利用Web后端监控对应的文件目录，从而可以允许用户从远程查看网络的监控数据。

TensorBoard 的使用需要模型代码和浏览器相互配合。在使用 TensorBoard 之前，需要安装 TensorBoard 库：

1 2	# 安装 TensorBoard pip install tensorboard

1.模型端

创建写入监控数据的Summary类，并在需要的时候写入监控数据即可。

首先通过tf.summary.create_file_writer创建监控对象类实例，并指定监控数据的写入目录

1 2	# 创建监控类，监控数据将写入 log_dir 目录 summary_writer = tf.summary.create_file_writer(log_dir)

例子：监控误差数据和可视化数据

在前向计算完成后，对于误差这种标量数据，我们通过tf.summary.scalar函数记录监控数据，并指定时间戳 step 参数

1
2
3

with summary_writer.as_default(): # 写入环境
    # 当前时间戳 step 上的数据为 loss，写入到名为 train-loss 数据库中
    tf.summary.scalar('train-loss', float(loss), step=step)

step：类似于每个数据对应的时间刻度信息（可以理解为数据曲线的x坐标），不宜重复。
每类数据通过字符串名字来区分，同类的数据需要写入相同名字的数据库中

对于图片类型的数据，可以通过tf.summary.image函数监控多个图片的张量数据，并通过设置max_outputs参数来选择最多显示的图片数量

with summary_writer.as_default():# 写入环境
    # 写入测试准确率
    tf.summary.scalar('test-acc', float(total_correct/total), step=step)
    # 可视化测试用的图片，设置最多可视化 9 张图片
    tf.summary.image("val-onebyone-images:", val_images, max_outputs=9, step=step)

2.浏览器端

打开 Web 后端：通过在 cmd 终端运行tensorboard --logdir path指定 Web 后端监控的文件目录 path，即可打开 Web 后端监控进程

之后打开浏览器，输入网址http://localhost:6006(也可通过 IP 地址远程访问，具体端口号可能会变动，可查看命令提示) 即可监控网络训练进度

除了监控标量数据和图片数据外， TensorBoard 还支持通过tf.summary.histogram查看张量数据的直方图分布，以及通过tf.summary.text打印文本信息等功能

with summary_writer.as_default():
    # 当前时间戳 step 上的数据为 loss，写入到 ID 位 train-loss 对象中
    tf.summary.scalar('train-loss', float(loss), step=step)
    # 可视化真实标签的直方图分布
    tf.summary.histogram('y-hist',y, step=step)
    # 查看文本信息
    tf.summary.text('loss-text',str(float(loss)))

实际上，除了 TensorBoard 外，Visdom 工具（具有更加丰富的可视化手段和实时性）同样可以方便可视化数据。Visdom 可以直接接受PyTorch 的张量类型的数据，但不能直接接受 TensorFlow 的张量类型数据，需要转换为Numpy 数组

五、过拟合

机器学习的主要目的是从训练集上学习到数据的真实模型，从而能够在未见过的测试集上也能够表现良好，我们把这种能力叫做泛化能力

1、模型的容量

通俗地讲，模型的容量或表达能力，是指模型拟合复杂函数的能力。一种体现模型容量的指标为模型的假设空间(Hypothesis Space)大小，即模型可以表示的函数集的大小。

假设空间越大越完备，从假设空间中搜索出逼近真实模型的函数也就越有可能；反之，如果假设空间非常受限，就很难从中找到逼近真实模型的函数

实际上，较大的假设空间并不一定能搜索出更好的函数模型。由于观测误差的存在，较大的假设空间中可能包含了大量表达能力过强的函数，能够将训练样本的观测误差也学习进来，从而伤害了模型的泛化能力。挑选合适容量的学习模型是一个很大的难题

2、过拟合与欠拟合

过拟合(Overfitting)：当模型的容量过大时，网络模型除了学习到训练集数据的模态之外，还把额外的观测误差也学习进来，导致学习的模型在训练集上面表现较好，但是在未见的样本上表现不佳，也就是模型泛化能力偏弱
欠拟合(Underfitting)：当模型的容量过小时，模型不能够很好地学习到训练集数据的模态，导致训练集上表现不佳，同时在未见的样本上表现也不佳

那么如何去选择模型的容量？

统计学习理论中的 VC 维度(Vapnik-Chervonenkis 维度)是一个应用比较广泛的度量函数容量的方法。但是该方法却很少应用到深度学习中去，一部分原因是神经网络过于复杂，很难去确定网络结构背后的数学模型的 VC 维度
可以根据奥卡姆剃刀原理(Occam’s razor)来指导神经网络的设计和训练。即“切勿浪费较多东西，去做‘用较少的东西，同样可以做好的事情’。”。也就是说，如果两层的神经网络结构能够很好的表达真实模型，那么三层的神经网络也能够很好的表达，但是我们应该优先选择使用更简单的两层神经网络，因为它的参数量更少，更容易训练，也更容易通过较少的训练样本获得不错的泛化误差

1.欠拟合

当我们发现当前的模型在训练集上出现：

误差一直维持较高的状态，很难优化减少
在测试集上表现也不佳

就应该考虑是否出现了欠拟合的现象

解决方法：

增加神经网络的层数
增大中间维度的大小

在实际使用过程中，更多的是出现过拟合现象

2.过拟合

现代深度神经网络中过拟合现象非常容易出现，主要是因为：

神经网络的表达能力非常强，
训练集样本数不够

3、数据集划分

前面我们介绍了数据集需要划分为训练集(Train set)和测试集(Test set)，但是为了挑选模型超参数和检测过拟合现象，一般需要将原来的训练集再次切分为新的训练集和验证集(Validation set)，即数据集需要切分为：

训练集：训练模型的参数
验证集：选择模型的超参数，提升模型的泛化能力
测试集：仅仅测试最后结果

1.验证集与超参数

验证集：选择模型的超参数(模型选择， Model selection)，功能包括：

根据验证集的性能表现来调整学习率、权值衰减系数、训练次数等
根据验证集的性能表现来重新调整网络拓扑结构
根据验证集的性能表现判断是否过拟合和欠拟合

训练集、验证集和测试集可以按着自定义的比例来划分，比如常见的 60%-20%-20%的划分

验证集与测试集的区别：

算法设计人员可以根据验证集的表现来调整模型的各种超参数的设置，提升模型的泛化能力（测试泛化性能）
测试集的表现不能用来反馈模型的调整，否则测试集将和验证集的功能重合，因此在测试集上的性能表现将无法代表模型的泛化能力

2.提前停止

一般把对训练集中的一个Batch运算更新一次叫做一个Step，对训练集的所有样本循环迭代一次叫做一个Epoch。验证集可以在数次 Step 或数次 Epoch 后使用，计算模型的验证性能（一般建议几个 Epoch 后进行一次验证运算）

训练时，一般关注的指标有训练误差、训练准确率等
验证时，也有验证误差和验证准确率等
测试时，也有测试误差和测试准确率等

通过观测训练准确率和验证准确率可以大致推断模型是否出现过拟合和欠拟合

过拟合：如果模型的训练误差较低，训练准确率较高，但是验证误差较高，验证准确率较低
- 解决方法：可以从新设计网络模型的容量，如降低网络的层数、降低网络的参数量、添加正则化手段、添加假设空间的约束等，使得模型的实际容量降低
欠拟合：如果训练集和验证集上面的误差都较高，准确率较低
- 解决方法：尝试增大网络的容量，如加深网络的层数、增加网络的参数量，尝试更复杂的网络结构

实际上，由于网络的实际容量可以随着训练的进行发生改变，因此在相同的网络设定下，随着训练的进行，可能观测到不同的过拟合、欠拟合状况

在训练的前期，随着训练的进行，模型的训练准确率和测试准确率都呈现增大的趋势，此时并没有出现过拟合现象
在训练后期，即使是相同网络结构下，由于模型的实际容量发生改变，我们观察到了过拟合的现象，具体表现为训练准确度继续改善，但是泛化能力变弱(测试准确率减低)

记录模型的验证准确率，并监控验证准确率的变化，当发现验证准确率连续𝑛个 Epoch 没有下降时，可以预测可能已经达到了最适合的 Epoch 附近，从而提前终止训练

4、模型设计

对于神经网络来说，网络的层数和参数量是网络容量很重要的参考指标

减少网络的层数，减少每层中网络参数量的规模，可以有效降低网络的容量
如果发现模型欠拟合，需要增大网络的容量，可以通过增加层数，增大每层的参数量等方式实现

5、正则化

通过设计不同层数、大小的网络模型可以为优化算法提供初始的函数假设空间，但是模型的实际容量可以随着网络参数的优化更新而产生变化。以多项式函数模型为例：

$y=\beta_{0}+\beta_{1} x+\beta_{2} x^{2}+\beta_{3} x^{3}+\cdots+\beta_{n} x^{n}+\varepsilon$

上述模型的容量可以通过n简单衡量。在训练的过程中，如果网络参数 $\beta_{k+1}, \cdots, \beta_{n}$ 均为0，那么网络的实际容量退化到k次多项式的函数容量。因此，通过限制网络参数的稀疏性，可以来约束网络的实际容量。

这种约束一般通过在损失函数上添加额外的参数稀疏性惩罚项实现，在未加约束之前的优化目标是：

$\min \mathcal{L}\left(f_{\theta}(\boldsymbol{x}), y\right),(\boldsymbol{x}, y) \in \mathbb{D}^{\text {train }}$

对模型的参数添加额外的约束后，优化的目标变为

$\min \mathcal{L}\left(f_{\theta}(\boldsymbol{x}), y\right)+\lambda \cdot \Omega(\theta),(\boldsymbol{x}, y) \in \mathbb{D}^{\text {train }}$

其中 $\Omega(\theta)$ 表示对网络参数 $\theta$ 的稀疏性约束函数。一般地，参数 $\theta$ 的稀疏性约束通过约束参数 $ \theta $ 的 $ L $ 范数实现，即：

$\Omega(\theta)=\sum_{\theta_{i}}\left\|\theta_{i}\right\|_{l}$

其中 $ \left|\theta_{i}\right|{l} $ 表示参数 $ \theta{i} $ 的 $l$ 范数。

新的优化目标除了要最小化原来的损失函数 $ \mathcal{L}(\boldsymbol{x}, y) $ 之外，还需要约束网络参数的稀疏性 $ \Omega(\theta) $，优化算法会在降低 $ \mathcal{L}(\boldsymbol{x}, y) $ 的同时，尽可能地迫使网络参数 $ \theta_{i} $ 变得稀疏，它们之间的权重关系通过超参数 $\lambda$ 来平衡。较大的 $\lambda$ 意味着网络的稀疏性更重要; 较小的 $\lambda$ 则意味着网络的训练误差更重要。通过选择合适的 $\lambda$ 超参数，可以获得较好的训练性能，同时保证网络的稀疏性，从而获得不错的泛化能力。

常用的正则化方式有 L0、L1、L2 正则化。

L0正则化

L0 正则化是指采用 $ \mathrm{L} 0 $ 范数作为稀疏性惩罚项 $ \Omega(\theta) $ 的正则化计算方式，即

$ \Omega(\theta)=\sum_{\theta_{i}}\left|\theta_{i}\right|_{0} $

其中 $ \mathrm{L} 0 $ 范数 $ \left|\theta_{i}\right|{0} $ 定义为 $ \theta{i} $ 中非零元素的个数。通过约束 $ \Sigma_{\theta_{i}}\left|\theta_{i}\right|{0} $ 的大小可以迫使网络中的连接权值大部分为 0，从而降低网络的实际参数量和网络容量。但是由于 $ \mathrm{L} 0 $ 范数 $ \left|\theta{i}\right|_{0} $ 并不可导，不能利用梯度下降算法进行优化，在神经网络中使用的并不多。

L1正则化

L1 正则化是指采用 $ \mathrm{L} 1 $ 范数作为稀疏性惩罚项 $ \Omega(\theta) $ 的正则化计算方式，即

$ \Omega(\theta)=\sum_{\theta_{i}}\left|\theta_{i}\right|_{1} $

其中 $ \mathrm{L} 1 $ 范数 $ \left|\theta_{i}\right|{1} $ 定义为张量 $ \theta{i} $ 中所有元素的绝对值之和。L1正则化也叫 Lasso Regularization，它是连续可导的，在神经网络中使用广泛

# 创建网络参数 w1,w2
w1 = tf.random.normal([4,3])
w2 = tf.random.normal([4,2])
# 计算 L1 正则化项
loss_reg = tf.reduce_sum(tf.math.abs(w1)) + tf.reduce_sum(tf.math.abs(w2))

L2正则化

L2 正则化是指采用 $ \mathrm{L} 2 $ 范数作为稀疏性惩罚项 $ \Omega(\theta) $ 的正则化计算方式，即

$ \Omega(\theta)=\sum_{\theta_{i}}\left|\theta_{i}\right|_{2} $

其中 $ \mathrm{L} 2 $ 范数 $ \left|\theta_{i}\right|{2} $ 定义为张量 $ \theta{i} $ 中所有元素的平方和。L2正则化也叫 Ridge Regularization，它是连续可导的，在神经网络中使用广泛

# 创建网络参数 w1,w2
w1 = tf.random.normal([4,3])
w2 = tf.random.normal([4,2])
# 计算 L2 正则化项
loss_reg = tf.reduce_sum(tf.square(w1)) + tf.reduce_sum(tf.square(w2))

6、Dropout

Dropout 通过随机断开神经网络的连接，减少每次训练时实际参与计算的模型的参数量；但是在测试时， Dropout 会恢复所有的连接，保证模型测试时获得最好的性能

在 TensorFlow 中，可以通过tf.nn.dropout(x, rate)函数实现某条连接的 Dropout 功能，其中 rate 参数设置断开的概率值𝑝

1 2	# 添加 dropout 操作，断开概率为 0.5 x = tf.nn.dropout(x, rate=0.5)

也可以将 Dropout 作为一个网络层使用，在网络中间插入一个 Dropout 层：

1 2	# 添加 Dropout 层，断开概率为 0.5 model.add(layers.Dropout(rate=0.5))

随着 Dropout 层的增加，网络模型训练时的实际容量减少，泛化能力变强

7、数据增强

增加数据集规模是解决过拟合最重要的途径。在有限的数据集上，通过数据增强技术可以增加训练的样本数量，获得一定程度上的性能提升

数据增强(Data Augmentation)是指在维持样本标签不变的条件下，根据先验知识改变样本的特征，使得新产生的样本也符合或者近似符合数据的真实分布

以图片数据为例。数据集中的图片大小往往是不一致的，为了方便神经网络处理，需要将图片缩放到某个固定的大小，如缩放后的固定224 × 224大小的图片。对于图中的人物图片，根据先验知识，我们知道旋转、缩放、平移、裁剪、改变视角、遮挡某局部区域都不会改变图片的主体类别标签，因此针对图片数据，可以有多种数据增强方式

TensorFlow 中提供了常用图片的处理函数，位于tf.image子模块中。通过tf.image.resize函数可以实现图片的缩放功能

将图片从文件系统读取进来后，即可进行图片数据增强操作。通过预处理：

def preprocess(x,y):
# 预处理函数
# x: 图片的路径， y：图片的数字编码
x = tf.io.read_file(x)
x = tf.image.decode_jpeg(x, channels=3) # RGBA
# 图片缩放到 244x244 大小，这个大小根据网络设定自行调整
x = tf.image.resize(x, [244, 244])

1.旋转

通过tf.image.rot90(x, k=1)可以实现图片按逆时针方式旋转 k 个 90 度

1 2	# 图片逆时针旋转 180 度 x = tf.image.rot90(x,2)

2.翻转

图片的翻转分为沿水平轴翻转和竖直轴翻转，可以通过tf.image.random_flip_left_right和tf.image.random_flip_up_down实现图片在水平方向和竖直方向的随机翻转操作

# 随机水平翻转
x = tf.image.random_flip_left_right(x)
# 随机竖直翻转
x = tf.image.random_flip_up_down(x)

3.裁剪

通过在原图的左右或者上下方向去掉部分边缘像素，可以保持图片主体不变，同时获得新的图片样本。在实际裁剪时，一般先将图片缩放到略大于网络输入尺寸的大小，再裁剪到合适大小

如网络的输入大小为224 × 224，那么可以先通过 resize 函数将图片缩放到244 × 244大小，再随机裁剪到224 × 224大小：

# 图片先缩放到稍大尺寸
x = tf.image.resize(x, [244, 244])
# 再随机裁剪到合适尺寸
x = tf.image.random_crop(x, [224,224,3])

4.生成数据

通过生成模型在原有数据上进行训练，学习到真实数据的分布，从而利用生成模型获得新的样本，这种方式也可以在一定程度上提升网络性能。如通过条件生成对抗网络(Conditional GAN,简称 CGAN)可以生成带标签的样本数据

5.其他方式

除了上述介绍的典型图片数据增强方式以外，可以根据先验知识，在不改变图片标签信息的条件下，任意变换图片数据，获得新的图片。如在原图上叠加高斯噪声、通过改变图片的观察视角后、在原图上随机遮挡部分区域等

8、过拟合问题

1.数据集构建

我们使用的数据集样本特性向量长度为 2，标签为 0 或 1，分别代表了两种类别。借助于scikit-learn库中提供的make_moons工具，我们可以生成任意多数据的训练集。首先安装 scikit-learn 库：

1 2	# pip 安装 scikit-learn 库 pip install -U scikit-learn

为了演示过拟合现象，采样1000个样本数据，同时添加标准差为 0.25 的高斯噪声数据：

# 导入数据集生成工具
from sklearn.datasets import make_moons
# 从 moon 分布中随机采样 1000 个点，并切分为训练集-测试集
X, y = make_moons(n_samples = N_SAMPLES, noise=0.25, random_state=100)
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = TEST_SIZE, random_state=42)

编写make_plot函数，方便根据样本的坐标 X 和样本的标签 y 绘制出数据的分布图：

def make_plot(X, y, plot_name, file_name, XX=None, YY=None, preds=None):
    plt.figure()
    # sns.set_style("whitegrid")
    axes = plt.gca()
    axes.set_xlim([x_min,x_max])
    axes.set_ylim([y_min,y_max])
    axes.set(xlabel="$x_1$", ylabel="$x_2$")
    # 根据网络输出绘制预测曲面
    if(XX is not None and YY is not None and preds is not None):
        plt.contourf(XX, YY, preds.reshape(XX.shape), 25, alpha = 0.08,
                     cmap=cm.Spectral)
        plt.contour(XX, YY, preds.reshape(XX.shape), levels=[.5],
                    cmap="Greys",
                    vmin=0, vmax=.6)
    # 绘制正负样本
    markers = ['o' if i == 1 else 's' for i in y.ravel()]
    mscatter(X[:, 0], X[:, 1], c=y.ravel(), s=20,
             cmap=plt.cm.Spectral, edgecolors='none', m=markers)
    # 保存矢量图
    plt.savefig(OUTPUT_DIR+'/'+file_name)

绘制出采样的 1000 个样本分布：

1 2	# 绘制数据集分布 make_plot(X, y, None, "dataset.svg")

2.网络层数的影响

为了探讨不同的网络深度下的过拟合程度，我们共进行了 5 次训练实验。在𝑛 ∈ [0,4]时，构建网络层数为𝑛 + 2层的全连接层网络，并通过 Adam 优化器训练 500 个 Epoch，获得网络在训练集上的分隔曲线

for n in range(5): # 构建 5 种不同层数的网络
    model = Sequential()# 创建容器
    # 创建第一层
    model.add(Dense(8, input_dim=2,activation='relu'))
    for _ in range(n): # 添加 n 层，共 n+2 层
        model.add(Dense(32, activation='relu'))
    model.add(Dense(1, activation='sigmoid')) # 创建最末层
    model.compile(loss='binary_crossentropy', optimizer='adam',
                  metrics=['accuracy']) # 模型装配与训练
    history = model.fit(X_train, y_train, epochs=N_EPOCHS, verbose=1)
    # 绘制不同层数的网络决策边界曲线
    preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
    title = "网络层数({})".format(n)
    file = "网络容量%f.png"%(2+n*1)
    make_plot(X_train, y_train, title, file, XX, YY, preds)

3.Dropout的影响

待添加

4.正则化的影响

待添加

六、卷积神经网络

1、全连接层的问题

全连接层较高的内存占用量严重限制了神经网络朝着更大规模、更深层数方向的发展

1.局部相关性

网络的每个输出节点都与所有的输入节点相连接，用于提取所有输入节点的特征信息，这种稠密的连接方式是全连接层参数量大、计算代价高的根本原因。全连接层也称为稠密连接层(Dense Layer)

全连接示意图

基于距离的重要性分布假设特性称为局部相关性，只关注和自己距离较近的部分节点，而忽略距离较远的节点。在这种重要性分布假设下，全连接层的连接模式变成了下图所示的状态，输出节点𝑗只与以𝑗为中心的局部区域(感受野)相连接，与其它像素无连接

局部链接的网络层示意图

其中和自己距离较近的部分节点形成的窗口称为感受野(Receptive Field)，表征了每个像素对于中心像素的重要性分布情况，网格内的像素才会被考虑，网格外的像素对于中心像素会被忽略

2.权值共享

如下图所示，在计算左上角位置的输出像素时，使用权值矩阵： $W=\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33} \end{bmatrix}$

与对应感受野内部的像素相乘累加，作为左上角像素的输出值；在计算右下方感受野区域时，共享权值参数𝑾，即使用相同的权值参数𝑾相乘累加，得到右下角像素的输出值，此时网络层的参数量只有3*3=9个，且与输入、输出节点数无关

劝值共享矩阵示意图

通过运用局部相关性和权值共享的思想，成功把网络的参数量减少到𝑘 × 𝑘(准确地说，是在单输入通道、单卷积核的条件下)。这种共享权值的“局部连接层”网络其实就是卷积神经网络

3.卷积运算

略

2、卷积神经网络

卷积神经网络通过充分利用局部相关性和权值共享的思想，大大地减少了网络的参数量，从而提高训练效率，更容易实现超大规模的深层网络

以图片数据为例，卷积层接受高、宽分别为ℎ、 𝑤，通道数为𝑐𝑖𝑛的输入特征图𝑿，在𝑐𝑜𝑢𝑡个高、宽都为𝑘，通道数为𝑐𝑖𝑛的卷积核作用下，生成高、宽分别为ℎ′、 𝑤′，通道数为𝑐𝑜𝑢𝑡的特征图输出。需要注意的是，卷积核的高宽可以不等，为了简化讨论，这里仅讨论高宽都为𝑘的情况

1.单通道输入和单卷积核

示意图

完成第一个感受野区域的特征提取后，感受野窗口向右移动一个步长单位(Strides，记为𝑠，默认为 1)

2.多通道输入和单卷积核

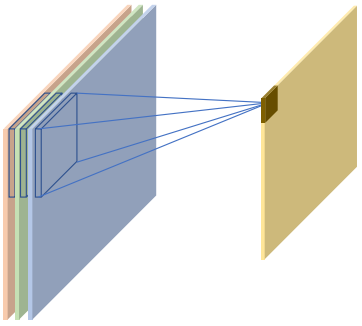
在多通道输入的情况下，卷积核的通道数需要和输入𝑿的通道数量相匹配，卷积核的第𝑖个通道和𝑿的第𝑖个通道运算，得到第𝑖个中间矩阵，此时可以视为单通道输入与单卷积核的情况，所有通道的中间矩阵对应元素再次相加，作为最终输出

多通道输入和单卷积核

整个的计算示意图如下所示，输入的每个通道处的感受野均与卷积核的对应通道相乘累加，得到与通道数量相等的中间变量，这些中间变量全部相加即得到当前位置的输出值。输入通道的通道数量决定了卷积核的通道数。 一个卷积核只能得到一个输出矩阵，无论输入𝑿的通道数量

多通道输入和单卷积核计算示意图

3.多通道输入、多卷积核

一般来说，一个卷积核只能完成某种逻辑的特征提取，当需要同时提取多种逻辑特征时，可以通过增加多个卷积核来得到多种特征，提高神经网络的表达能力，这就是多通道输入、多卷积核的情况

当出现多卷积核时，第𝑖 ( $i \in [1,n]$ ， 𝑛为卷积核个数)个卷积核与输入𝑿运算得到第𝑖个输出矩阵(也称为输出张量𝑶的通道𝑖），最后全部的输出矩阵在通道维度上进行拼接(Stack 操作，创建输出通道数的新维度)，产生输出张量𝑶， 𝑶包含了𝑛个通道数

即： n个卷积核得到n个输出矩阵（通道数），无论输入𝑿的通道数量

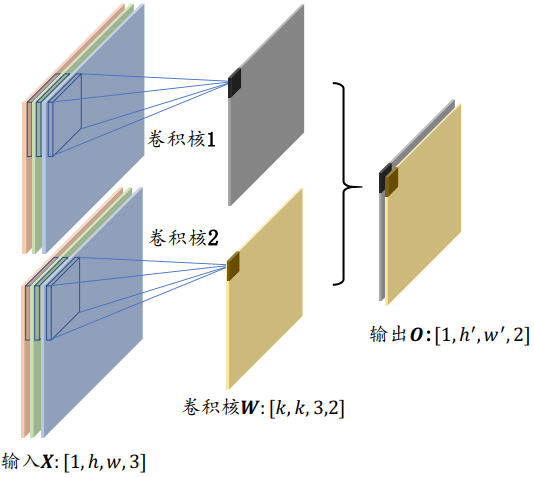
多卷积核示意图

每个卷积核的大小𝑘、步长𝑠、填充设定等都是统一设置（保证输出的每个通道大小一致）

4.步长

感受野密度的控制手段一般是通过移动步长(Strides)实现的

步长是指感受野窗口每次移动的长度单位，对于2D输入来说，分为沿𝑥(向右)方向和𝑦(向下)方向的移动长度

当步长设计的较小时，感受野以较小幅度移动窗口，有利于提取到更多的特征信息，输出张量的尺寸也更大
当步长设计的较大时，感受野以较大幅度移动窗口，有利于减少计算代价，过滤冗余信息，输出张量的尺寸也更小

5.填充

在网络模型设计时，有时希望输出𝑶的高宽能够与输入𝑿的高宽相同，从而方便网络参数的设计、残差连接等

方法：通过在原输入𝑿的高和宽维度上面进行填充(Padding)若干无效元素操作，得到增大的输入𝑿′。通过精心设计填充单元的数量，在𝑿′上面进行卷积运算得到输出𝑶的高宽可以和原输入𝑿相等，甚至更大

卷积神经层的输出尺寸 $[b,h',w',c_{out}]$ 由卷积核的数量 $c_{out}$ ，卷积核的大小𝑘，步长𝑠，填充数𝑝(只考虑上下填充数量 $p_h$ 相同，左右填充数量 $p_w$ 相同的情况)以及输入𝑿的高宽ℎ/𝑤共同决定，它们之间的数学关系可以表达为：

$h'=\left \lfloor \frac{h+2\cdot p_h-k}{s} \right \rfloor+1$

$w'=\left \lfloor \frac{w+2\cdot p_w-k}{s} \right \rfloor+1$

其中 $p_h$ 、 $p_w$ 分别表示高、宽方向的填充数量
$s$ 为卷积移动步长
$k$ 为卷积核大小（这里假设卷积核为 $k*k$ ）
$\left \lfloor \right \rfloor$ 表示向下取整

在 TensorFlow 中，在𝑠 = 1 时，如果希望输出𝑶和输入𝑿高、宽相等，只需要简单地设置参数 padding="SAME" 即可使 TensorFlow 自动计算 padding 数量

3、卷积层实现

在 TensorFlow 中，既可以通过自定义权值的底层实现方式搭建神经网络，也可以直接调用现成的卷积层类的高层方式快速搭建复杂网络

1.自定义权值

通过tf.nn.conv2d函数可以方便地实现 2D 卷积运算。tf.nn.conv2d基于输入 $X:[b,h,w,c_{in}]$ 和卷积核 $W:[k,k,c_{in},c_{out}]$ 进行卷积运算，得到输出 $O:[b,h',w',c_{out}]$

$c_{in}$ ：输入通道数
$c_{out}$ ：卷积核的数量，即输出特征图的通道数
$k$ ：卷积核宽高
$b$ ：图片数量

>>> x = tf.random.normal([2,5,5,3]) # 模拟输入， 3 通道，高宽为 5
# 需要根据[k,k,cin,cout]格式创建 W 张量， 4 个 3x3 大小卷积核
>>> w = tf.random.normal([3,3,3,4])
# 步长为 1, padding 为 0,
>>> out = tf.nn.conv2d(x,w,strides=1,padding=[[0,0],[0,0],[0,0],[0,0]])
# 输出张量的 shape
TensorShape([2, 3, 3, 4])

padding参数格式：padding=[[0,0],[上,下],[左,右],[0,0]]

1 2	# 上下左右各填充一个单位： padding=[[0,0],[1,1],[1,1],[0,0]]

特别地，通过设置参数padding='SAME'、strides=1可以直接得到输入、输出同大小的卷积层

当strides>1时，设置padding='SAME'将使得输出高、宽将成 $\frac{1}{strides}$ 倍地减少

>>> x = tf.random.normal([2,5,5,3])
>>> w = tf.random.normal([3,3,3,4])
# 高宽先 padding 成可以整除 3 的最小整数 6，然后 6 按 3 倍减少，得到 2x2
>>> out = tf.nn.conv2d(x,w,strides=3,padding='SAME')
TensorShape([2, 2, 2, 4])

卷积神经网络层与全连接层一样，可以设置网络带偏置向量。tf.nn.conv2d函数是没有实现偏置向量计算的，添加偏置需要手动累加偏置张量：

# 根据[cout]格式创建偏置向量
>>> b = tf.zeros([4])
# 在卷积输出上叠加偏置向量，它会自动 broadcasting 为[b,h',w',cout]
>>> out = out + b

2.卷积层类

通过卷积层类layers.Conv2D可以直接调用类实例完成卷积层的前向计算（TensorFlow中，API的首字母大写的对象一般表示类，全部小写的一般表示函数）。使用类方式会自动创建（在创建类时或build时）需要的权值张量和偏置向量等，用户不需要记忆卷积核张量的定义格式

在新建卷积层类时，只需要指定卷积核数量参数filters，卷积核大小kernel_size，步长strides，填充 padding 等即可

1 2	# 创建了 4 个3 × 3大小的卷积核的卷积层，步长为 1，padding 方案为'SAME' layer = layers.Conv2D(4,kernel_size=3,strides=1,padding='SAME')

卷积核数量即为输出特征图的通道数

如果卷积核高宽不等，步长行列方向不等，此时需要将kernel_size参数设计为元组格式 $(k_h,k_w)$ ，strides参数设计为 $(s_h,s_w)$

1 2	# 创建 4 个3 × 4大小的卷积核，竖直方向移动步长𝑠ℎ = 2，水平方向移动步长𝑠𝑤 = 1： layer = layers.Conv2D(4,kernel_size=(3,4),strides=(2,1),padding='SAME')

创建完成后，通过调用实例(的__call__方法)即可完成前向计算：

# 创建卷积层类
>>> layer = layers.Conv2D(4,kernel_size=3,strides=1,padding='SAME')
>>> out = layer(x) # 前向计算
>>> out.shape # 输出张量的 shape
TensorShape([2, 5, 5, 4])

在类Conv2D中，可以通过类成员trainable_variables直接返回𝑾和𝒃的列表：

# 返回所有待优化张量列表
>>> layer.trainable_variables
[<tf.Variable 'conv2d/kernel:0' shape=(3, 3, 3, 4) dtype=float32, numpy=
 array([[[[ 0.13485974, -0.22861657, 0.01000655, 0.11988598],
          [ 0.12811887, 0.20501086, -0.29820845, -0.19579397],
          [ 0.00858489, -0.24469738, -0.08591779, -0.27885547]], ...
 <tf.Variable 'conv2d/bias:0' shape=(4,) dtype=float32, numpy=array([0., 0., 0., 0.], dtype=float32)>]

可以直接调用类实例layer.kernel、layer.bias名访问𝑾和𝒃张量

4、LeNet-5实战

1990 年代， Yann LeCun 等人提出了用于手写数字和机器打印字符图片识别的神经网络，被命名为 LeNet-5。 LeNet-5 的提出，使得卷积神经网络在当时能够成功被商用，广泛应用在邮政编码、支票号码识别等任务中

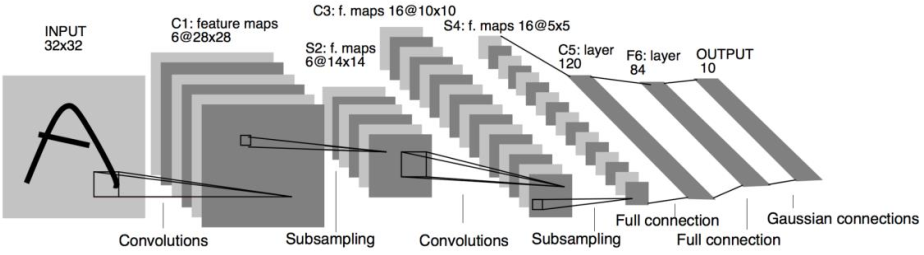
LeNet-5网络结构

接受32*32大小的数字、字符图片，经过第一个卷积层得到[b,28,28,6]形状的张量，经过一个向下采样层，张量尺寸缩小到[b,14,14,6]
经过第二个卷积层，得到[b,10,10,16]形状的张量，同样经过下采样层，张量尺寸缩小到[b,5,5,16]
在进入全连接层之前，先将张量打成[b,400]的张量
送入输出节点数分别为120、84的2个全连接层，得到[b,84]的张量
最后通过Gaussian connections层

在上述基础上进行少许调整，使得它更容易在现代深度学习框架上实现：

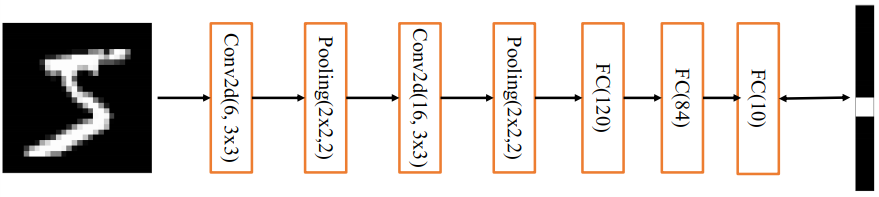
调整后的网络结构

将输入𝑿形状由32 × 32调整为28 × 28
将 2 个下采样层实现为最大池化层(降低特征图的高、宽，后续会介绍)
利用全连接层替换掉Gaussian connections层

加载MNIST数据集：进阶操作 -> 7、经典数据集加载

创建网络：

from tensorflow.keras import Sequential
network = Sequential([ # 网络容器
    layers.Conv2D(6,kernel_size=3,strides=1), # 第一个卷积层, 6 个 3x3 卷积核
    layers.MaxPooling2D(pool_size=2,strides=2), # 高宽各减半的池化层
    layers.ReLU(), # 激活函数
    layers.Conv2D(16,kernel_size=3,strides=1), # 第二个卷积层, 16 个 3x3 卷积核
    layers.MaxPooling2D(pool_size=2,strides=2), # 高宽各减半的池化层
    layers.ReLU(), # 激活函数
    layers.Flatten(), # 打平层，方便全连接层处理
    layers.Dense(120, activation='relu'), # 全连接层， 120 个节点
    layers.Dense(84, activation='relu'), # 全连接层， 84 节点
    layers.Dense(10) # 全连接层， 10 个节点
])
# build 一次网络模型，给输入 X 的形状，其中 4 为随意给的 batchsz
network.build(input_shape=(4, 28, 28, 1))
# 统计网络信息
network.summary()

网络信息如下：

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              multiple                  60        
_________________________________________________________________
max_pooling2d (MaxPooling2D) multiple                  0         
_________________________________________________________________
re_lu (ReLU)                 multiple                  0         
_________________________________________________________________
conv2d_1 (Conv2D)            multiple                  880       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 multiple                  0         
_________________________________________________________________
re_lu_1 (ReLU)               multiple                  0         
_________________________________________________________________
flatten (Flatten)            multiple                  0         
_________________________________________________________________
dense (Dense)                multiple                  48120     
_________________________________________________________________
dense_1 (Dense)              multiple                  10164     
_________________________________________________________________
dense_2 (Dense)              multiple                  850       
=================================================================
Total params: 60,074
Trainable params: 60,074
Non-trainable params: 0
_________________________________________________________________

卷积神经网络可以降低特征维度，同时显著降低网络参数量，增加网络深度

5、表示学习

图片数据的识别过程一般认为也是表示学习（Representation Learning）的过程，从接受到的原始像素特征开始，逐渐提取边缘、角点等底层特征，再到纹理等中层特征，再到头部、物体部件等高层特征，最后的网络层基于这些学习到的抽象特征表示（ Representation）做分类逻辑的学习。学习到的特征越高层、越准确，就越有利于分类器的分类，从而获得较好的性能。从表示学习的角度来理解，卷积神经网络通过层层堆叠来逐层提取特征，网络训练的过程可以看成特征的学习过程，基于学习到的高层抽象特征可以方便地进行分类任务。

应用表示学习的思想，训练好的卷积神经网络往往能够学习到较好的特征，这种特征的提取方法一般是通用的。比如在猫、狗任务上学习到头、脚、身躯等特征的表示，在其它动物上也能够一定程度上使用。基于这种思想，可以将在任务A上训练好的深层神经网络的前面数个特征提取层迁移到任务B上，只需要训练任务B的分类逻辑（表现为网络的最末数层），即可取得非常好的效果，这种方式是迁移学习的一种，从神经网络角度也称为网络微调（Fine- tuning）。

6、梯度传播

考虑一简单的情形，输入为3×3的单通道矩阵，与一个2×2的卷积核，进行卷积运算，输岀结果打平后直接与虚构的标注计算误差，如下所示：

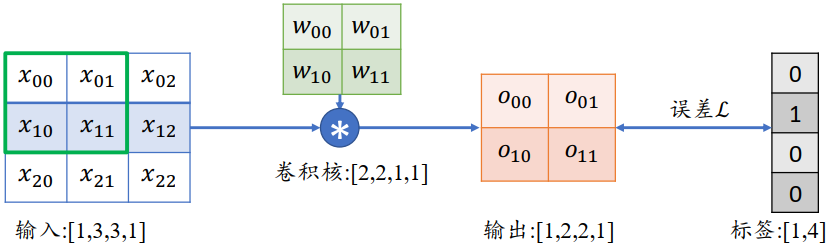
卷积层梯度传播

首先推导出输出张量 $O$ 的表达形式：

$\begin{aligned} o_{00} &=x_{00} w_{00}+x_{01} w_{01}+x_{10} w_{10}+x_{11} w_{11}+b \\ o_{01} &=x_{01} w_{00}+x_{02} w_{01}+x_{11} w_{10}+x_{12} w_{11}+b \\ o_{10} &=x_{10} w_{00}+x_{11} w_{01}+x_{20} w_{10}+x_{21} w_{11}+b \\ o_{11} &=x_{11} w_{00}+x_{12} w_{01}+x_{21} w_{10}+x_{22} w_{11}+b \end{aligned}$

以 $w_{00}$ 的梯度计算为例，通过链式法则分解：

$\frac{\partial \mathcal{L}}{\partial w_{00}}=\sum_{i \in\{00,01,10,11\}} \frac{\partial \mathcal{L}}{\partial o_{i}} \frac{\partial o_{i}}{\partial w_{00}}$

其中 $ \frac{\partial \mathcal{L}}{\partial o_{i}} $ 可直接由误差函数推导出来，我们直接来考虑 $ \frac{\partial O_{i}}{\partial w_{i}} $ ，例如 :

$\frac{\partial o_{00}}{\partial w_{00}}=\frac{\partial\left(x_{00} w_{00}+x_{01} w_{01}+x_{10} w_{10}+x_{11} w_{11}+b\right)}{w_{00}}=x_{00}$

同样的方法有：

$\begin{array}{l} \frac{\partial o_{01}}{\partial w_{00}}=\frac{\partial\left(x_{01} w_{00}+x_{02} w_{01}+x_{11} w_{10}+x_{12} w_{11}+b\right)}{w_{00}}=x_{01} \\ \frac{\partial o_{10}}{\partial w_{00}}=\frac{\partial\left(x_{10} w_{00}+x_{11} w_{01}+x_{20} w_{10}+x_{21} w_{11}+b\right)}{w_{00}}=x_{10} \\ \frac{\partial o_{11}}{\partial w_{00}}=\frac{\partial\left(x_{11} w_{00}+x_{12} w_{01}+x_{21} w_{10}+x_{22} w_{11}+b\right)}{w_{00}}=x_{11} \end{array}$

可以观察到，通过循环移动感受野的方式并没有改变网络层可导性，同时梯度的推导也并不复杂，只是当网络层数增大以后，人工梯度推导将变得十分的繁琐。不过深度学习框架可以自动完成所有参数的梯度计算与更新，我们只需要设计好网络结构即可

7、池化层

在卷积层中，可以通过调节步长参数𝑠实现特征图的高宽成倍缩小，从而降低了网络的参数量。实际上，除了通过设置步长，还有一种专门的网络层可以实现尺寸缩减功能，即池化层（ Pooling Layer）

池化层同样基于局部相关性的思想，通过从局部相关的一组元素中进行采样或信息聚合，从而得到新的元素值。特别地：

最大池化层（ Max Pooling）从局部相关元素集中选取最大的一个元素值
平均池化层（ Average Pooling）从局部相关元素集中计算平均值并返回

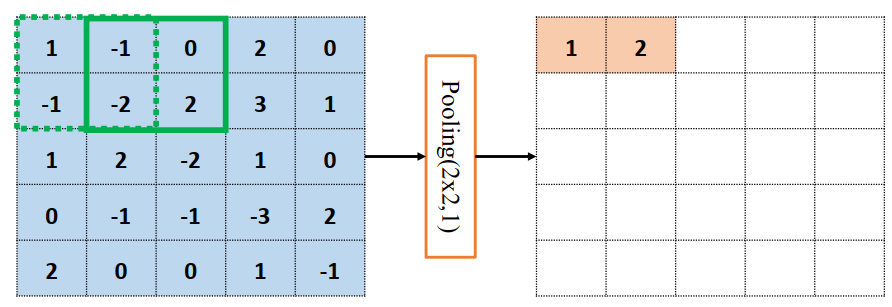
以5×5输入 $X$ 的最大池化层为例，假设池化感受野窗口大小𝑘=2，步长𝑠=1的情况，如下所示。绿色虚线方框代表第一个感受野的位置，此时输出结果为$$x^{\prime}=\max ({1,-1,-1,-2})=1$$，并以此类推整个池化过程

由于池化层没有需要学习的参数，计算简单，并且可以有效减低特征图的尺寸，非常适合图片这种类型的数据，在计算机视觉相关任务中得到了广泛的应用。

通过精心设计池化层感受野的高宽𝑘和步长𝑠参数，可以实现各种降维运算

8、BatchNorm层

卷积神经网络的出现，网络参数量大大减低，使得几十层的深层网络成为可能。然而，在残差网络出现之前，网络的加深使得网络训练变得非常不稳定，甚至出现网络长时间不更新甚至不收敛的现象，同时网络对超参数比较敏感，超参数的微量扰动也会导致网络的训练轨迹完全改变

2015年， Google研究人员 Sergey roffe等提出了一种参数标准化（ Normalize）的手段并基于参数标准化设计了 Batch nomalization（简写为 BatchNorn，或BN）层。BN层的提出，使得网络的超参数的设定更加自由，比如更大的学习率、更随意的网络初始化等，同时网络的收敛速度更快，性能也更好。BN层提岀后便广泛地应用在各种深度网络模型上，卷积层、BN层、ReLU层、池化层一度成为网络模型的标配单元块，通过堆叠Conv-BN-ReLU-Pooling方式往往可以获得不错的模型性能。

在 TensorFlow中，通过 layers.BatchNormalization()类可以非常方便地实现BN层：

1 2	# 创建 BN 层 layer=layers.BatchNormalization()

与全连接层、卷积层不同，BN层的训练阶段和测试阶段的行为不同，需要通过设置training标志位来区分训练模式还是测试模式

以 LeNet5的网络模型为例，在卷积层后添加BN层，代码如下：

network = Sequential([ # 网络容器
    layers.Conv2D(6,kernel_size=3,strides=1),
    # 插入 BN 层
    layers.BatchNormalization(),
    layers.MaxPooling2D(pool_size=2,strides=2),
    layers.ReLU(),
    layers.Conv2D(16,kernel_size=3,strides=1),
    # 插入 BN 层
    layers.BatchNormalization(),
    layers.MaxPooling2D(pool_size=2,strides=2),
    layers.ReLU(),
    layers.Flatten(),
    layers.Dense(120, activation='relu'),
    # 此处也可以插入 BN 层
    layers.Dense(84, activation='relu'),
    # 此处也可以插入 BN 层
    layers.Dense(10)
])

在训练阶段，需要设置网络的参数 training=True 以区分 BN 层是训练还是测试模型：

with tf.GradientTape() as tape:
    # 插入通道维度
    x = tf.expand_dims(x,axis=3)
    # 前向计算，设置计算模式， [b, 784] => [b, 10]
    out = network(x, training=True)

在测试阶段，需要设置 training=False，避免 BN 层采用错误的行为：

for x,y in db_test: # 遍历测试集
    # 插入通道维度
    x = tf.expand_dims(x,axis=3)
    # 前向计算，测试模式
    out = network(x, training=False)

9、经典卷积网络

自2012年 AlexNet 的提出以来，各种各样的深度卷积神经网络模型相继被提出，其中比较有代表性的有ⅤGG系列， Goog LeNet系列， ResNet系列， DenseNet系列等，他们的网络层数整体趋势逐渐增多。

1.AlexNet

2012年， ILSVRC12挑战赛 ImageNet 数据集分类任务的冠军 Alex Krichevsky 提出了8层的深度神经网络模型 AlexNet，它接收输入为224×224大小的彩色图片数据，经过五个卷积层和三个全连接层后得到样本属于1000个类别的概率分布。为了降低特征图的维度， AlexNet在第1、2、5个卷积层后添加了 Max Pooling层，如下图所示，网络的参数量达到了6000万个：

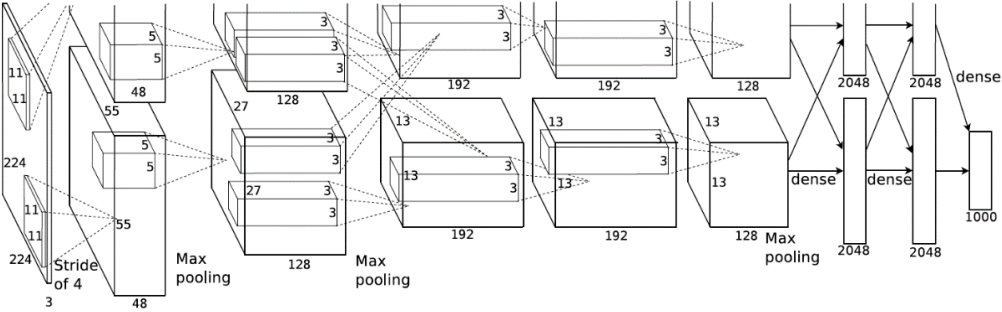
AlexNet网络结构

AlexNet的创新之处在于

层数达到了较深的8层
采用了ReLU激活函数，过去的神经网络大多采用Sigmoid激活函数，计算相对复杂，容易出现梯度弥散现象
引入Dropout层。Dropout提高了模型的泛化能力，防止过拟合

2.VGG系列

2014年， ILSVRCI4挑战赛 ImageNet分类任务的亚军牛津大学ⅤGG实验室提出了ⅤGGI1、 VGG13、ⅤGGl6、VGG19等一系列的网络模型，并将网络深度最高提升至19层。

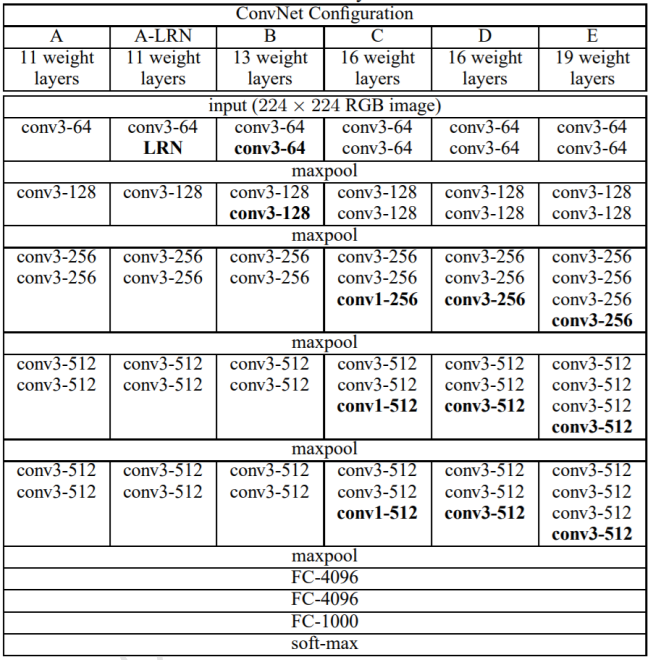
VGG系列网络结构配置

以GG16为例，它接受224×224大小的彩色图片数据，经过2个Conv-Conv-Pooling单元，和3个Conv- Conv-ConV- Pooling单元的堆叠，最后通过3层全连接层输出当前图片分别属于1000类别的概率分布

VGG16网络结构

VGG系列网络的创新之处在于：

层数提升至19层
全部釆用更小的3×3卷积核，相对于 AlexNet 中7×7的卷积核，参数量更少，计算代价更低
采用更小的池化层2×2窗口和步长s=2，而 AlexNet中是3×3的池化窗口和步长s=2

3.GoogLeNet

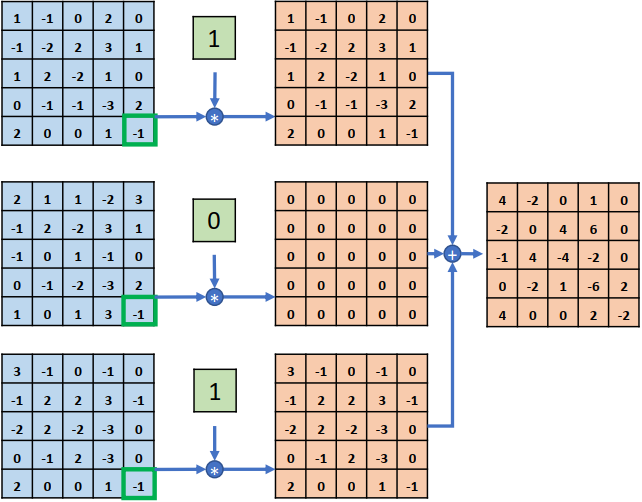
3×3的卷积核参数量更少，计算代价更低，同时在性能表现上甚至更优越，因此业界开始探索卷积核最小的情况：1×1卷积核。

如下所示，输入为3通道的5×5图片，与单个1×1的卷积核进行卷积运算，每个通道的数据与对应通道的卷积核运算，得到 3个通道的中间矩阵，对应位置相加得到最终的输出张量。对于输入shape为[b,h,w,Cin]， 1x1卷积层的输出为[b,h,w,Cout]，其中cin为输入数据的通道数，cout为输出数据的通道数，也是1×1卷积核的数量。

1×1卷积核的一个特别之处在于，它可以不改变特征图的宽高，而只对通道数c进行变换。

1*1卷积核示意图

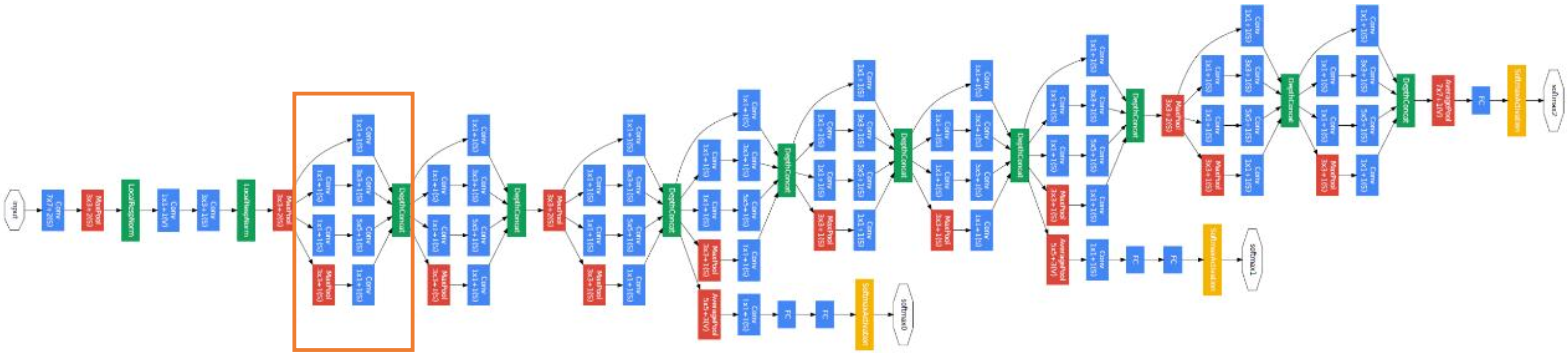
2014年，ILSVRC14挑战赛的冠军Google提出了大量采用3×3和1×1卷积核的网络模型： GoogLeNet，网络层数达到了22层。虽然GoogLeNet的层数远大于AlexNet, 但是它的参数量却只有AlexNet的1/12，同时性能也远好于AlexNet。

GoogLeNet网络采用模块化设计的思想，通过大量堆叠Inception模块，形成了复杂的网络结构。如下所示，Inception模块的输入为X，通过4个子网络得到4个网络输出，在通道轴上面进行拼接合并，形成Inception模块的输出。这4个子网络是：

1×1卷积层
1×1卷积层，再通过一个3×3卷积层
1×1卷积层，再通过一个5×5卷积层
3×3最大池化层，再通过1×1卷积层

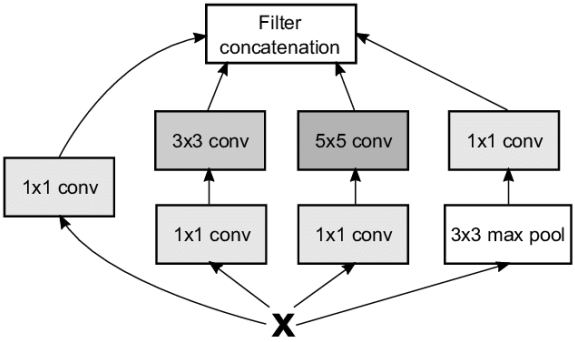
Inception模块

GoogLeNet 的网络结构如下所示，其中红色框中的网络结构即为Inception模块的网络结构：

GoogLeNet网络结构

10、CIFAR10与VGG13实战

CIFAR10 数据集由加拿大 Canadian Institute For Advanced Research 发布，它包含了飞机、汽车、鸟、猫等共 10 大类物体的彩色图片，每个种类收集了 6000 张32 × 32大小图片，共 6 万张图片。其中 5 万张作为训练数据集， 1 万张作为测试数据集。

在 TensorFlow 中，不需要手动下载、解析和加载 CIFAR10 数据集，通过 datasets.cifar10.load_data() 函数就可以直接加载切割好的训练集和测试集

CIFAR10图片识别任务并不简单，这主要是由于CIFAR10的图片内容需要大量细节才能呈现，而保存的图片分辨率仅有32×32，使得部分主体信息较为模糊。浅层的神经网络表达能力有限，很难训练优化到较好的性能，这里将基于表达能力更强的VGG13网络，并根据数据集特点修改部分网络结构，完成CIFAR10图片识别。修改如下：

将网络输入调整为32×32。原网络输入为224×224，导致全连接层输入特征维度过大，网络参数量过大
3个全连接层的维度调整为[256,64,10]，满足10分类任务的设定

import  tensorflow as tf
from    tensorflow.keras import layers, optimizers, datasets, Sequential
import  os

os.environ['TF_CPP_MIN_LOG_LEVEL']='2'  # 消除调用显卡警告
tf.random.set_seed(2345)

conv_layers = [ # 5 units of conv + max pooling
    # unit 1
    # 64 个 3x3 卷积核, 输入输出同大小
    layers.Conv2D(64, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.Conv2D(64, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same'),# 高宽减半

    # unit 2
    # 输出通道提升至 128，高宽大小减半
    layers.Conv2D(128, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.Conv2D(128, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same'),

    # unit 3
    # 输出通道提升至 256，高宽大小减半
    layers.Conv2D(256, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.Conv2D(256, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same'),

    # unit 4
    # 输出通道提升至 512，高宽大小减半
    layers.Conv2D(512, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.Conv2D(512, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same'),

    # unit 5
    # 输出通道提升至 512，高宽大小减半
    layers.Conv2D(512, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.Conv2D(512, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
    layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same')
]
# 预处理
def preprocess(x, y):
    # [0~1]
    x = 2*tf.cast(x, dtype=tf.float32) / 255.-1
    y = tf.cast(y, dtype=tf.int32)
    return x,y

(x,y), (x_test, y_test) = datasets.cifar10.load_data()  # 在线下载，加载 CIFAR10 数据集
y = tf.squeeze(y, axis=1)  # 删除 y 的一个维度， [b,1] => [b]
y_test = tf.squeeze(y_test, axis=1)
print(x.shape, y.shape, x_test.shape, y_test.shape)  # 打印训练集和测试集的形状
# 训练集的𝑿和𝒚形状为：(50000, 32, 32, 3)和(50000)，测试集的𝑿和𝒚形状为(10000, 32, 32, 3)和(10000)

# 构建训练集对象，随机打乱，预处理，批量化
train_db = tf.data.Dataset.from_tensor_slices((x,y))
train_db = train_db.shuffle(1000).map(preprocess).batch(128)
# 构建测试集对象，预处理，批量化
test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test))
test_db = test_db.map(preprocess).batch(64)
# 从训练集中采样一个 Batch， 并观察
sample = next(iter(train_db))
print('sample:', sample[0].shape, sample[1].shape,
      tf.reduce_min(sample[0]), tf.reduce_max(sample[0]))

def main():
    # [b, 32, 32, 3] => [b, 1, 1, 512]
    conv_net = Sequential(conv_layers)  # 利用前面创建的层列表构建网络容器
	# 创建 3 层全连接层子网络
    fc_net = Sequential([
        layers.Dense(256, activation=tf.nn.relu),
        layers.Dense(128, activation=tf.nn.relu),
        layers.Dense(10, activation=None),
    ])
	# build2 个子网络，并打印网络参数信息
    conv_net.build(input_shape=[None, 32, 32, 3])
    fc_net.build(input_shape=[None, 512])
    conv_net.summary()
    fc_net.summary()
    optimizer = optimizers.Adam(lr=1e-4)

    # [1, 2] + [3, 4] => [1, 2, 3, 4]
    # 由于将网络实现为 2 个子网络，在进行梯度更新时，需要合并 2 个子网络的待优化参数列表
    variables = conv_net.trainable_variables + fc_net.trainable_variables

    for epoch in range(50):
        for step, (x,y) in enumerate(train_db):
            with tf.GradientTape() as tape:
                # [b, 32, 32, 3] => [b, 1, 1, 512]
                out = conv_net(x)
                # flatten, => [b, 512]
                out = tf.reshape(out, [-1, 512])
                # [b, 512] => [b, 10]
                logits = fc_net(out)
                # [b] => [b, 10]
                y_onehot = tf.one_hot(y, depth=10)
                # compute loss
                loss = tf.losses.categorical_crossentropy(y_onehot, logits, from_logits=True)
                loss = tf.reduce_mean(loss)

            grads = tape.gradient(loss, variables)  # 对所有参数求梯度
            optimizer.apply_gradients(zip(grads, variables))  # 自动更新

            if step %100 == 0:
                print(epoch, step, 'loss:', float(loss))

        total_num = 0
        total_correct = 0
        for x,y in test_db:

            out = conv_net(x)
            out = tf.reshape(out, [-1, 512])
            logits = fc_net(out)
            prob = tf.nn.softmax(logits, axis=1)
            pred = tf.argmax(prob, axis=1)
            pred = tf.cast(pred, dtype=tf.int32)

            correct = tf.cast(tf.equal(pred, y), dtype=tf.int32)
            correct = tf.reduce_sum(correct)

            total_num += x.shape[0]
            total_correct += int(correct)

        acc = total_correct / total_num
        print(epoch, 'acc:', acc)  # 计算一遍epoch的测试准确率

if __name__ == '__main__':
    main()

11、卷积层变种

1.空洞卷积

普通的卷积层为了减少网络的参数量，卷积核的设计通常选择较小的1×1和3×3感受野大小。小卷积核使得网络提取特征时的感受野区域有限，但是增大感受野的区域又会增加网络的参数量和计算代价，因此需要权衡设计

空洞卷积（Dilated/Atrous Convolution)的提出较好地解决这个问题，空洞卷积在普通卷积的感受野上增加一个Dilation Rate参数，用于控制感受野区域的采样步长，如下所示：

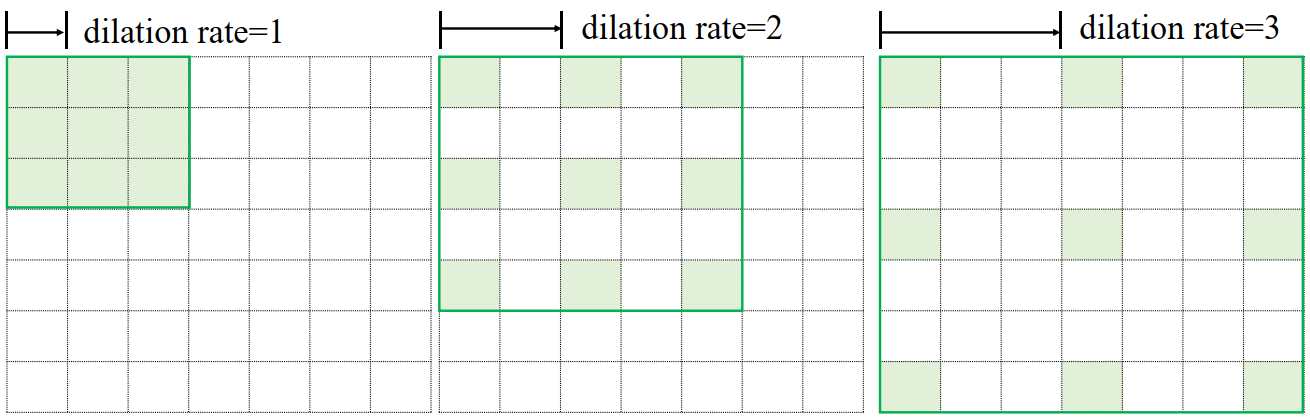
感受野采样步长示意图

当感受野的采样步长Dilation Rate为1时，每个感受野采样点之间的距离为 1，此时的空洞卷积退化为普通的卷积
当Dilation Rate为2时，感受野每2个单元采样一个点，如上图中间的绿色方框中绿色格子所示，每个采样格子之间的距离为2
如上图右边的Dilation Rate为3，采样步长为3

尽管Dilation Rate的增大会使得感受野区域增大，但是实际参与运算的点数仍然保持不变

空洞卷积在不增加网络参数的条件下，提供了更大的感受野窗口。但是在使用空洞卷积设置网络模型时，需要精心设计Dilation Rate参数来避免出现网格效应，同时较大的 Dilation Rate 参数并不利于小物体的检测、语义分割等任务

在TensorFlow中，可以通过设置layers.Conv2D()类的dilation_rate参数来选择使用普通卷积还是空洞卷积：

x = tf.random.normal([1,7,7,1]) # 模拟输入
# 空洞卷积， 1 个 3x3 的卷积核
layer = layers.Conv2D(1,kernel_size=3,strides=1,dilation_rate=2)
out = layer(x) # 前向计算
out.shape
# 输出: TensorShape([1, 3, 3, 1])

2.转置卷积

转置卷积(Transposed Convolution 或 Fractionally Strided Convolution）：通过在输入之间填充大量的padding来实现输出高宽大于输入高宽的效果，从而实现向上采样的目的

部分资料也称之为反卷积(Deconvolution)，实际上反卷积在数学上定义为卷积的逆过程，但转置卷积并不能恢复出原卷积的输入，因此称为反卷积并不妥当

转置卷积仅仅能够恢复原原始数据的大小（shape，即形状相同），但是不能还原原始数据，即：

原始数据(5x5) --> 3x3卷积核，步长为2 --> 卷积后数据(2x2)
卷积后数据(2x2) --> 转置卷积 --> 原始数据(5x5)，但是此时数据已经不同

转置卷积输出与输入关系可以根据以下情况分两种来看：

1. $o+2p-k$ 为 $s$ 倍数

在 $o+2p-k$ 为 $s$ 倍数时，转置卷积输出与输入关系为：

$o=(i-1)s+k-2p$

$o$ ：转置卷积输出大小
$i$ ：转置卷积输入大小
$s$ ：转置卷积的步长
$k$ ：转置卷积核大小
$p$ ：填充大小

2. $o+2p-k$ 不为 $s$ 倍数

由于在普通的卷积运算中，有：

$o=\left\lfloor\frac{i+2 * p-k}{s}\right]+1$

$o$ ：卷积输出大小
$i$ ：卷积输入大小
$s$ ：卷积的步长
$k$ ：卷积核大小
$p$ ：填充大小

此时当步长 $s>1$ 时，向下取整运算使得出现多种不同输入尺寸 𝑖 对应到相同的输出尺寸 𝑜 上。因此，不同输入大小的卷积运算可能获得相同大小的输出。

考虑到卷积与转置卷积输入输出大小关系互换，从转置卷积的角度来说，输入尺寸 i 经过转置卷积运算后，可能获得不同的输出 o 大小。因此转置卷积也需要相应的调整：

$o=(i-1)s+k-2p+a$

其中$$a=(o+2p-k)%s$$

$o$ ：转置卷积输出大小
$i$ ：转置卷积输入大小
$s$ ：转置卷积的步长
$k$ ：转置卷积核大小
$p$ ：填充大小

在 TensorFlow 中不需要手动指定𝑎参数，只需要指定输出尺寸即可， TensorFlow 会自动推导需要填充的行列数𝑎，前提是输出尺寸合法：

# 恢复出 6x6 大小
# out为[1,2,2,1] w为[3,3,1,1]
xx = tf.nn.conv2d_transpose(out, w, strides=2,
                            padding='VALID',
                            output_shape=[1,6,6,1])

转置卷积的卷积核的定义格式为 [𝑘, 𝑘, 𝑐𝑜𝑢𝑡, 𝑐𝑖𝑛]
不支持自定义 padding 设置，只能设置为 VALID 或者 SAME
- VALID：输出大小表达为 $o=(i-1)s+k-2p+a$
- SAME：输出大小表达为 $o=i.s$
通过改变参数 output_shape=[1,5,5,1]也可以获得高宽为 5×5 的张量

例子：

# 创建 4x4 大小的输入
x = tf.range(16)+1
x = tf.reshape(x,[1,4,4,1])
x = tf.cast(x, tf.float32)
# 创建 3x3 卷积核
w = tf.constant([[-1,2,-3.],[4,-5,6],[-7,8,-9]])
w = tf.expand_dims(w,axis=2)
w = tf.expand_dims(w,axis=3)
# 普通卷积运算
out = tf.nn.conv2d(x,w,strides=1,padding='VALID')

# 输出
<tf.Tensor: id=42, shape=(2, 2), dtype=float32, numpy=
    array([[-56., -61.],
           [-76., -81.]], dtyp

恢复：

# 恢复 4x4 大小的输入
xx = tf.nn.conv2d_transpose(out, w, strides=1, padding='VALID',
                            output_shape=[1,4,4,1])
tf.squeeze(xx)

# 输出
<tf.Tensor: id=44, shape=(4, 4), dtype=float32, numpy=
    array([[ 56., -51., 46., 183.],
           [-148., -35., 35., -123.],
           [ 88., 35., -35., 63.],
           [ 532., -41., 36., 729.]], dtype=float32)>

转置卷积也可以和其他层一样，通过 layers.Conv2DTranspose 类创建一个转置卷积层，然后调用实例即可完成前向计算：

1 2	layer = layers.Conv2DTranspose(1,kernel_size=3,strides=1,padding='VALID') xx2 = layer(out) # 通过转置卷积层

矩阵角度

转置卷积的转置是指卷积核矩阵W产生的稀疏矩阵W’在计算过程中需要先转置 $W^{'T}$ ，再进行矩阵相乘运算，而普通卷积并没有转置W’的步骤。这也是它被称为转置卷积的名字由来

考虑普通Conv2d运算：X和W，需要根据步长s将卷积核在行、列方向循环移动获取参与运算的感受野的数据，串行计算每个窗口处的“相乘累加”值计算效率极低。为了加速运算，在数学上可以将卷积核W根据步长s重排成稀疏矩阵W’，再通过W’@X’一次完成运算(实际上，W’矩阵过于稀疏，导致很多无用的0乘运算，很多深度学习框架也不是通过这种方式实现的)

转置卷积具有“放大特征图”的功能，在生成对抗网络、语义分割等中得到了广泛应用，如DCGAN中的生成器通过堆叠转置卷积层实现逐层“放大”特征图，最后获得十分逼真的生成图片。

3.分离卷积

这里以深度可分离卷积(Depth-wise Separable Convolution)为例。普通卷积在对多通道输入进行运算时，卷积核的每个通道与输入的每个通道分别进行卷积运算，得到多通道的特征图，再对应元素相加产生单个卷积核的最终输出

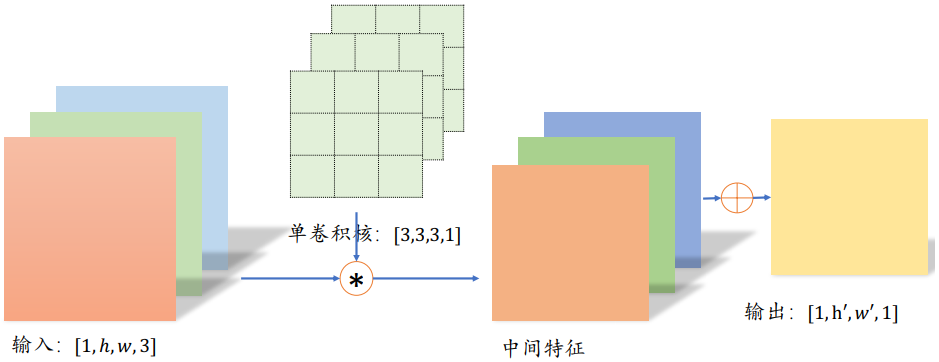
普通卷积计算

分离卷积的计算流程则不同，卷积核的每个通道与输入的每个通道进行卷积运算，得到多个通道的中间特征，如下所示。这个多通道的中间特征张量接下来进行多个1×1卷积核的普通卷积运算，得到多个高宽不变的输出，这些输出在通道轴上面进行拼接，从而产生最终的分离卷积层的输出。可以看到，分离卷积层包含了两步卷积运算，第一步卷积运算是单个卷积核，第二个卷积运算包含了多个卷积核。

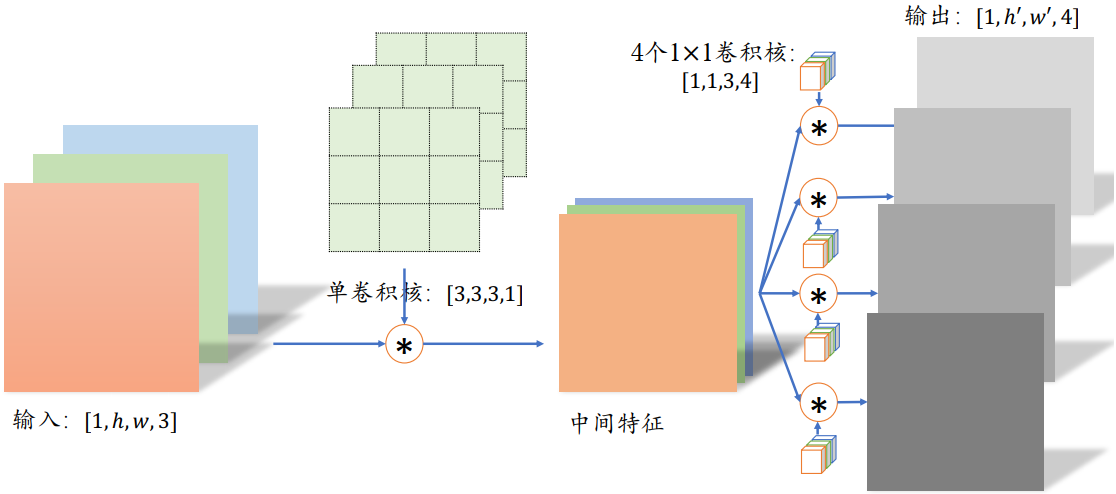
深度可分离卷积计算

同样的输入和输出，采用 Separable Convolution的参数量约是普通卷积的1/3。

考虑上图中的普通卷积和分离卷积的例子。

普通卷积的参数量是 3·3·3·4=108

分离卷积的第一部分参数量是 3·3·3·1=27。第二部分参数量是 1·1·3·4=14。总参数量只有39，但是却能实现普通卷积同样的输入输出尺寸变换。

分离卷积在Xception和MobileNets等对计算代价敏感的领域中得到了大量应用

12、深度残差网络

研究人员发现网络的层数越深，越有可能获得更好的泛化能力。但是当模型加深以后，网络变得越来越难训练，这主要是由于梯度弥散和梯度爆炸现象造成的。（在较深层数的神经网络中，梯度信息由网络的末层逐层传向网络的首层时，传递的过程中会出现梯度接近于0或梯度值非常大的现象。网络层数越深，这种现象可能会越严重）

通过在输入和输出之间添加一条直接连接的Skip Connection可以让神经网络具有回退的能力。以VGG13深度神经网络为例，假设观察到VGG13模型出现梯度弥散现象，而 10 层的网络模型并没有观测到梯度弥散现象，那么可以考虑在最后的两个卷积层添加Skip Connection，如下所示。通过这种方式，网络模型可以自动选择是否经由这两个卷积层完成特征变换，还是直接跳过这两个卷积层而选择Skip Connection，亦或结合两个卷积层和Skip Connection的输出。

添加Skip Connection的VGG13

2015年，微软亚洲研究院何凯明等人发表了基于Skip Connection的深度残差网络 (Residual Neural Network，简称ResNet)算法，并提出了18层、34层、50层、101 层、152层的ResNet-18、ResNet-34、ResNet-50、ResNet-101和ResNet-152等模型，甚至成功训练出层数达到1202层的极深层神经网络。

1.ResNet原理

ResNet通过在卷积层的输入和输出之间添加Skip Connection实现层数回退机制：

残差模块

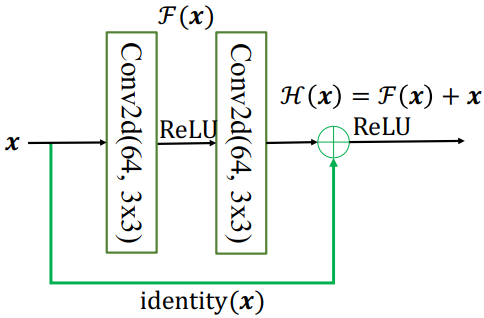
输入x通过两个卷积层，得到特征变换后的输出F(x)，与输入x进行对应元素的相加运算，得到最终输出H(x)：

$\mathcal{H}(\boldsymbol{x})=\boldsymbol{x}+\mathcal{F}(\boldsymbol{x})$

叫作残差模块(Residual Block，简称ResBlock)。由于被 Skip Connection 包围的卷积神经网络需要学习映射 $\mathcal{F}(\boldsymbol{x})=\mathcal{H}(\boldsymbol{x})-\boldsymbol{x}$ ，故称为残差网络。

为了能够满足输入x与卷积层的输出F(x)能够相加运算，需要输入x的shape与F(x)的 shape 完全一致。当出现shape不一致时，一般通过在 Skip Connection 上添加额外的卷积运算环节将输入x变换到与F(x)相同的shape，如上图中identity(x)函数所示，其中 identity(x)以1x1的卷积运算居多，主要用于调整输入的通道数

2.ResBlock实现

深度残差网络并没有增加新的网络层类型，只是通过在输入和输出之间添加一条Skip Connection，因此并没有针对ResNet的底层实现。

在TensorFlow中通过调用普通卷积层即可实现残差模块

class BasicBlock(layers.Layer):  # 残差模块类
    def __init__(self, filter_num, stride=1):
        super(BasicBlock, self).__init__()
        # f(x)包含了 2 个普通卷积层，创建卷积层 1
        self.conv1 = layers.Conv2D(filter_num, (3, 3), strides=stride, padding='same')
        self.bn1 = layers.BatchNormalization()
        self.relu = layers.Activation('relu')
        # 创建卷积层 2
        self.conv2 = layers.Conv2D(filter_num, (3, 3), strides=1, padding='same')
        self.bn2 = layers.BatchNormalization()
	    # 当ℱ(𝒙)的形状与𝒙不同时，无法直接相加，需要新建identity(𝒙)卷积层，来完成𝒙的形状转换
        if stride != 1:  # 插入 identity 层
            self.downsample = Sequential()
            self.downsample.add(layers.Conv2D(filter_num, (1, 1), strides=stride))
        else:  # 否则，直接连接
            self.downsample = lambda x:x
            
    def call(self, inputs, training=None):  # 前向传播函数
        out = self.conv1(inputs) # 通过第一个卷积层
        out = self.bn1(out)
        out = self.relu(out)
        out = self.conv2(out) # 通过第二个卷积层
        out = self.bn2(out)
        # 输入通过 identity()转换
        identity = self.downsample(inputs)
        # f(x)+x 运算
        output = layers.add([out, identity])
        # 再通过激活函数并返回
        output = tf.nn.relu(output)
        return output

13、DenseNet

DenseNet将前面所有层的特征图信息通过Skip Connection与当前层输出进行聚合，与ResNet的对应位置相加方式不同，DenseNet采用在通道轴c维度进行拼接操作，聚合特征信息。

如下所示，输入 $X_0$ 通过 $H_1$ 卷积层得到输出 $X_1$ ， $X_1$ 与 $X_0$ 在通道轴上进行拼接，得到聚合后的特征张量，送入 $H_2$ 卷积层，得到输出 $X_2$ ，同样的方法， $X_2$ 与前面所有层的特征信息 $X_1$ 与 $X_0$ 进行聚合，再送入下一层。如此循环，直至最后一层的输出 $X_4$ 和前面所有层的特征信息： $\{X_i\}_{i=0,1,2,3}$ 进行聚合得到模块的最终输出。这样一种基于Skip Connection 稠密连接的模块叫做Dense Block

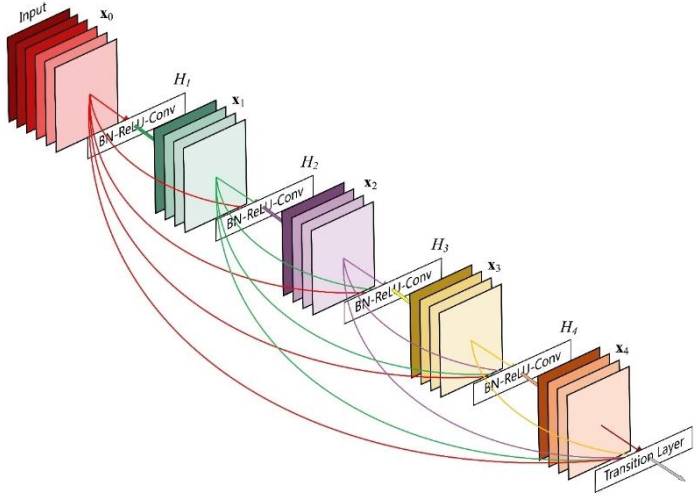
Dense Block结构

DenseNet 通过堆叠多个 Dense Block 构成复杂的深层神经网络：

典型DenseNet结构

14、CIFAR10与ResNet18实战

标准的 ResNet18 接受输入为 22 × 22 大小的图片数据，这里将 ResNet18 进行适量调整，使得它输入大小为32 × 32，输出维度为 10。调整后的 ResNet18 网络结构如下所示

调整后的ResNet18

网络实现：

import  tensorflow as tf
from    tensorflow import keras
from    tensorflow.keras import layers, Sequential



class BasicBlock(layers.Layer):  # 残差模块
    def __init__(self, filter_num, stride=1):
        super(BasicBlock, self).__init__()
        # 第一个卷积单元
        self.conv1 = layers.Conv2D(filter_num, (3, 3), strides=stride, padding='same')
        self.bn1 = layers.BatchNormalization()
        self.relu = layers.Activation('relu')
        # 第二个卷积单元
        self.conv2 = layers.Conv2D(filter_num, (3, 3), strides=1, padding='same')
        self.bn2 = layers.BatchNormalization()

        if stride != 1:# 通过1x1卷积完成shape匹配
            self.downsample = Sequential()
            self.downsample.add(layers.Conv2D(filter_num, (1, 1), strides=stride))
        else:# shape匹配，直接短接
            self.downsample = lambda x:x

    def call(self, inputs, training=None):  # 前向计算函数
        # [b, h, w, c]，通过第一个卷积单元
        out = self.conv1(inputs)
        out = self.bn1(out)
        out = self.relu(out)
        # 通过第二个卷积单元
        out = self.conv2(out)
        out = self.bn2(out)
        # 通过identity模块
        identity = self.downsample(inputs)
        # 2条路径输出直接相加
        output = layers.add([out, identity])
        output = tf.nn.relu(output) # 激活函数
        return output


class ResNet(keras.Model):
    # 通用的ResNet实现类
    def __init__(self, layer_dims, num_classes=10): # [2, 2, 2, 2]
        super(ResNet, self).__init__()
        # 根网络，预处理
        self.stem = Sequential([layers.Conv2D(64, (3, 3), strides=(1, 1)),
                                layers.BatchNormalization(),
                                layers.Activation('relu'),
                                layers.MaxPool2D(pool_size=(2, 2), strides=(1, 1), padding='same')
                                ])
        # 堆叠4个Block，每个block包含了多个BasicBlock,设置步长不一样
        self.layer1 = self.build_resblock(64,  layer_dims[0])
        self.layer2 = self.build_resblock(128, layer_dims[1], stride=2)
        self.layer3 = self.build_resblock(256, layer_dims[2], stride=2)
        self.layer4 = self.build_resblock(512, layer_dims[3], stride=2)

        # 通过Pooling层将高宽降低为1x1
        self.avgpool = layers.GlobalAveragePooling2D()
        # 最后连接一个全连接层分类
        self.fc = layers.Dense(num_classes)

    def call(self, inputs, training=None):
        # 通过根网络
        x = self.stem(inputs)
        # 一次通过4个模块
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        x = self.layer4(x)

        # 通过池化层
        x = self.avgpool(x)
        # 通过全连接层
        x = self.fc(x)

        return x



    def build_resblock(self, filter_num, blocks, stride=1):
        # 辅助函数，堆叠filter_num个BasicBlock
        res_blocks = Sequential()
        # 只有第一个BasicBlock的步长可能不为1，实现下采样
        res_blocks.add(BasicBlock(filter_num, stride))

        for _ in range(1, blocks):#其他BasicBlock步长都为1
            res_blocks.add(BasicBlock(filter_num, stride=1))

        return res_blocks


def resnet18():
    # 通过调整模块内部BasicBlock的数量和配置实现不同的ResNet
    return ResNet([2, 2, 2, 2])


def resnet34():
     # 通过调整模块内部BasicBlock的数量和配置实现不同的ResNet
    return ResNet([3, 4, 6, 3])

在设计深度卷积神经网络时，一般按照特征图高宽ℎ/𝑤逐渐减少，通道数𝑐逐渐增大的经验法则

训练：

import  tensorflow as tf
from    tensorflow.keras import layers, optimizers, datasets, Sequential
import  os
from    resnet import resnet18

os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
tf.random.set_seed(2345)





def preprocess(x, y):
    # 将数据映射到-1~1
    x = 2*tf.cast(x, dtype=tf.float32) / 255. - 1
    y = tf.cast(y, dtype=tf.int32) # 类型转换
    return x,y


(x,y), (x_test, y_test) = datasets.cifar10.load_data() # 加载数据集
y = tf.squeeze(y, axis=1) # 删除不必要的维度
y_test = tf.squeeze(y_test, axis=1) # 删除不必要的维度
print(x.shape, y.shape, x_test.shape, y_test.shape)


train_db = tf.data.Dataset.from_tensor_slices((x,y)) # 构建训练集
# 随机打散，预处理，批量化
train_db = train_db.shuffle(1000).map(preprocess).batch(512)

test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test)) #构建测试集
# 随机打散，预处理，批量化
test_db = test_db.map(preprocess).batch(512)
# 采样一个样本
sample = next(iter(train_db))
print('sample:', sample[0].shape, sample[1].shape,
      tf.reduce_min(sample[0]), tf.reduce_max(sample[0]))


def main():

    # [b, 32, 32, 3] => [b, 1, 1, 512]
    model = resnet18() # ResNet18网络
    model.build(input_shape=(None, 32, 32, 3))
    model.summary() # 统计网络参数
    optimizer = optimizers.Adam(lr=1e-4) # 构建优化器

    for epoch in range(100): # 训练epoch

        for step, (x,y) in enumerate(train_db):

            with tf.GradientTape() as tape:
                # [b, 32, 32, 3] => [b, 10],前向传播
                logits = model(x)
                # [b] => [b, 10],one-hot编码
                y_onehot = tf.one_hot(y, depth=10)
                # 计算交叉熵
                loss = tf.losses.categorical_crossentropy(y_onehot, logits, from_logits=True)
                loss = tf.reduce_mean(loss)
            # 计算梯度信息
            grads = tape.gradient(loss, model.trainable_variables)
            # 更新网络参数
            optimizer.apply_gradients(zip(grads, model.trainable_variables))

            if step %50 == 0:
                print(epoch, step, 'loss:', float(loss))



        total_num = 0
        total_correct = 0
        for x,y in test_db:

            logits = model(x)
            prob = tf.nn.softmax(logits, axis=1)
            pred = tf.argmax(prob, axis=1)
            pred = tf.cast(pred, dtype=tf.int32)

            correct = tf.cast(tf.equal(pred, y), dtype=tf.int32)
            correct = tf.reduce_sum(correct)

            total_num += x.shape[0]
            total_correct += int(correct)

        acc = total_correct / total_num
        print(epoch, 'acc:', acc)



if __name__ == '__main__':
    main()

七、循环神经网络

卷积神经网络利用数据的局部相关性和权值共享的思想大大减少了网络的参数量，非常适合于图片这种具有空间(Spatial)局部相关性的数据，已经被成功地应用到计算机视觉领域的一系列任务上。自然界的信号除了具有空间维度之外，还有一个时间（Temporal）维度。具有时间维度的信号非常常见，比如我们正在阅读的文本、说话时发出的语音信号、随着时间变化的股市参数等。这类数据并不一定具有局部相关性，同时数据在时间维度上的长度也是可变的，卷积神经网络并不擅长处理此类数据

1、序列表示方法

能够直接用一个标量数值表示出来的可以通过一个shape：[b,s]来表示，其中b为序列数量，s为序列长度。但是很多信号并不能用一个标量数值来表示，如每个时间戳产生长度为n的特征向量，此时着需要shape为[b,s,n]的张量来表示

而更复杂的文本数据着不能通过某个标量来表示。对于一本含有n个单词的句子，可以通过前面介绍的One-hot编码来表示，如下所示为𝑛个地名的单词，可以将每个地名编码为长度为𝑛的 Onehot 向量：

地名One-hot编码方案

把文字编码为数值的过程叫作Word Embedding。One-hot的编码方式实现Word Embedding简单直观，编码过程不需要学习和训练。但One-hot编码的向量是高维度而且极其稀疏的，大量的位置为0，计算效率较低，同时也不利于神经网络的训练。从语义角度来讲，One-hot编码还忽略了单词先天具有的语义相关性，不能很好地体现原有文字的语义相关度。

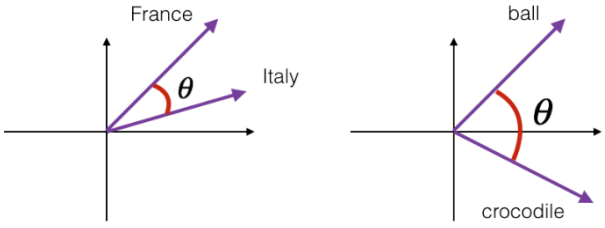
在自然语言处理领域，有专门的一个研究方向在探索如何学习到单词的表示向量（Word Vector)，使得语义层面的相关性能够很好地通过Word Vector体现出来。一个衡量词向量之间相关度的方法就是余弦相关度（Cosine similarity)：

$\operatorname{similarity}(\boldsymbol{a}, \boldsymbol{b}) \triangleq \cos (\theta)=\frac{\boldsymbol{a} \cdot \boldsymbol{b}}{|\boldsymbol{a}| \cdot|\boldsymbol{b}|}$

其中a和b代表了两个词向量。下图演示了单词“France”和“Italy”的相似度，以及单词“ball”和“crocodile”的相似度， $\theta$ 为两个词向量之间的夹角。可以看到余弦相关度较好地反映了语义相关性。

余弦相似度示意图

1.Embedding层

在神经网络中，单词的表示向量可以直接通过训练的方式得到，我们把单词的表示层叫作Embedding层。Embedding层负责把单词编码为某个词向量v，它接受的是采用数字编码的单词编号 $i$ （如2表示“I”，3表示“me”等），系统总单词数量记为 $N_{vocab}$ ，输出长度为n的向量v：

$\boldsymbol{v}=f_{\theta}\left(i \mid N_{\mathrm{vocab}}, n\right)$

Embedding 层实现起来非常简单，构建一个 shape 为 $[𝑁_{vocab}, 𝑛]$ 的查询表对象 table，对于任意的单词编号𝑖，只需要查询到对应位置上的向量并返回即可：

$𝒗 = 𝑡𝑎𝑏𝑙𝑒[𝑖]$

Embedding 层是可训练的，它可放置在神经网络之前，完成单词到向量的转换，得到的表示向量可以继续通过神经网络完成后续任务，并计算误差ℒ，采用梯度下降算法来实现端到端(end-to-end)的训练。

在 TensorFlow 中，可以通过 layers.Embedding(𝑁vocab,𝑛)来定义一个 Word Embedding 层：

𝑁vocab：词汇数量
𝑛：单词向量的长度

x = tf.range(10) # 生成 10 个单词的数字编码
x = tf.random.shuffle(x) # 打散
# 创建共 10 个单词，每个单词用长度为 4 的向量表示的层
net = layers.Embedding(10, 4)
out = net(x) # 获取词向量
# 些词向量随机初始化的，尚未经过网络训练
<tf.Tensor: id=96, shape=(10, 4), dtype=float32, numpy=
array([[-0.00998075, -0.04006485, 0.03493755, 0.03328368],
 [-0.04139598, -0.02630153, -0.01353856, 0.02804044],…

net.embeddings # 直接查看 Embedding 层内部的查询表 table
<tf.Variable 'embedding_4/embeddings:0' shape=(10, 4) dtype=float32, numpy=
array([[ 0.04112223, 0.01824595, -0.01841902, 0.00482471],
 [-0.00428962, -0.03172196, -0.04929272, 0.04603403],…

net.embeddings.trainable # 查看 net.embeddings 张量的可优化属性
True# 可以通过梯度下降算法优化

2.预训练的词向量

Embedding 层的查询表是随机初始化的，需要从零开始训练。实际上可以使用预训练的 Word Embedding 模型来得到单词的表示方法，基于预训练模型的词向量相当于迁移了整个语义空间的知识，往往能得到更好的性能。

目前应用的比较广泛的预训练模型有 Word2Vec 和 GloVe 等。它们已经在海量语料库训练得到了较好的词向量表示方法，并可以直接导出学习到的词向量表，方便迁移到其它任务。如 GloVe 模型 GloVe.6B.50d，词汇量为 40 万，每个单词使用长度为 50 的向量表示，用户只需要下载对应的模型文件即可，“glove6b50dtxt.zip”模型文件约 69MB。

对于 Embedding 层，不再采用随机初始化的方式，而是利用已经预训练好的模型参数去初始化：

# 从预训练模型中加载词向量表
embed_glove = load_embed('glove.6B.50d.txt')
# 直接利用预训练的词向量表初始化 Embedding 层
net.set_weights([embed_glove])

经过预训练的词向量模型初始化的 Embedding 层可以设置为不参与训练：net.trainable = False，那么预训练的词向量就直接应用到此特定任务上。

如果希望能够学到区别于预训练词向量模型不同的表示方法，那么可以把 Embedding 层包含进反向传播算法中去，利用梯度下降来微调单词表示方法。

2、循环卷积网络

现在来考虑处理一个序列信号，以文本序列为例，考虑一个句子：

“I hate this boring movie”

通过 Embedding 层，可以将它转换为 shape 为[𝑏, 𝑠, 𝑛]的张量（上述句子可以表示为 shape 为[1,5,10]的张量）：

𝑏：句子数量
𝑠：句子长度
𝑛：词向量长度

接下来逐步探索能够处理序列信号的网络模型，为了便于表达，我们以情感分类任务为例，如下图所示。

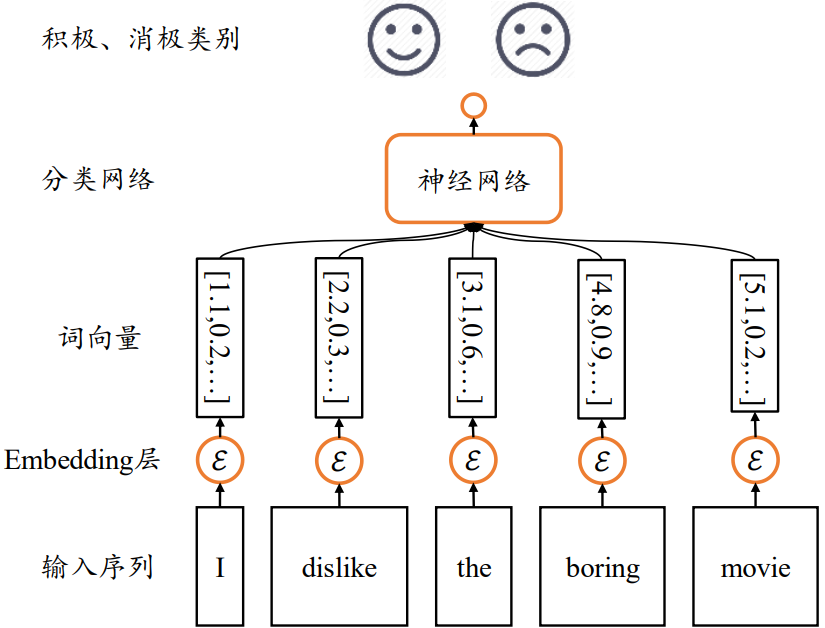
感情分类任务

情感分类任务通过分析给出的文本序列，提炼出文本数据表达的整体语义特征，从而预测输入文本的情感类型：正面评价或者负面评价。但是由于输入是文本序列（与图片分类不一样），传统的卷积神经网络并不能取得很好的效果（没有考虑时间的连续）

1.全连接层？

如果对于每个词向量，分别使用一个全连接层网络 𝒐 = 𝜎(𝑾_𝑡𝒙_𝑡 + 𝒃_𝑡) 提取语义特征，各个单词的词向量通过𝑠个全连接层分类网络 1 提取每个单词的特征，所有单词的特征最后合并，并通过分类网络 2 输出序列的类别概率分布。但是：

对长度为𝑠的句子来说，至少需要𝑠个全网络层，参数量较大，且每个序列长度s并不相同，网络是动态变化的
每个全连接层子网络 $𝑾_𝑖$ 和 $𝒃_𝑖$ 只能感受当前词向量的输入，并不能感知之前和之后的语境信息，导致句子整体语义的缺失，每个子网络只能根据自己的输入来提取高层特征

2.共享权值

在处理序列信号的问题上，可以借助卷积神经网络中共享权值的思想来减少网络的参数量。

𝑠个全连接层的网络并没有实现权值同享。这里将这𝑠个网络层参数共享，这样其实相当于使用一个全连接网络来提取所有单词的特征信息：

网络模型

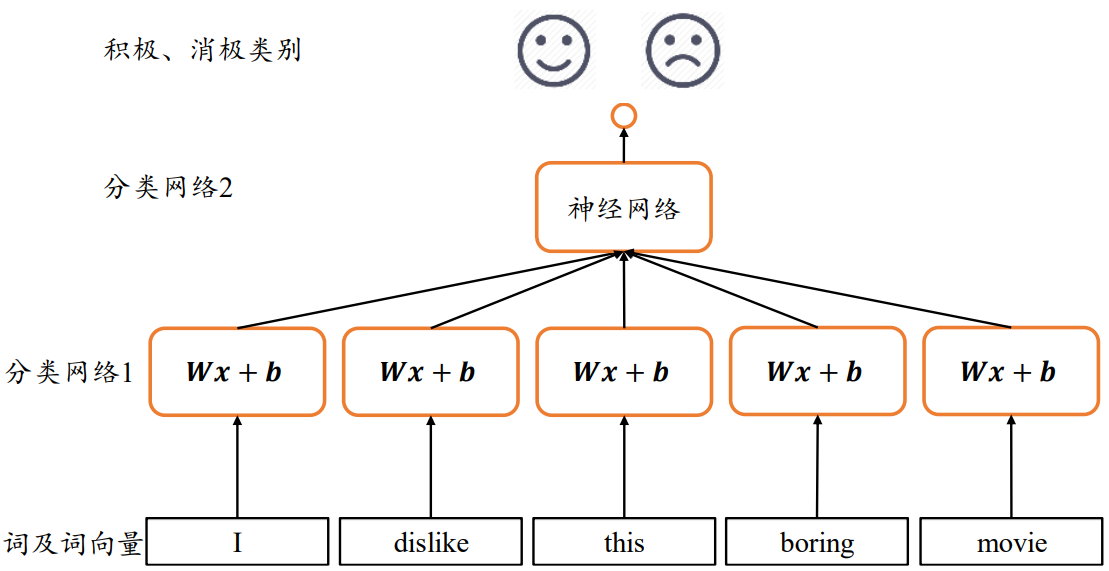
但是这并没有考虑序列之间的先后顺序，将词向量打乱次序仍然能获得相同的输出，无法获取有效的全局语义信息

3.全局语义

可以利用内存(Memory)机制解决该问题：网络提供一个单独的内存变量，每次提取词向量的特征并刷新内存变量，直至最后一个输入完成，此时的内存变量即存储了所有序列的语义特征，并且由于输入序列之间的先后顺序，使得内存变量内容与序列顺序紧密关联。

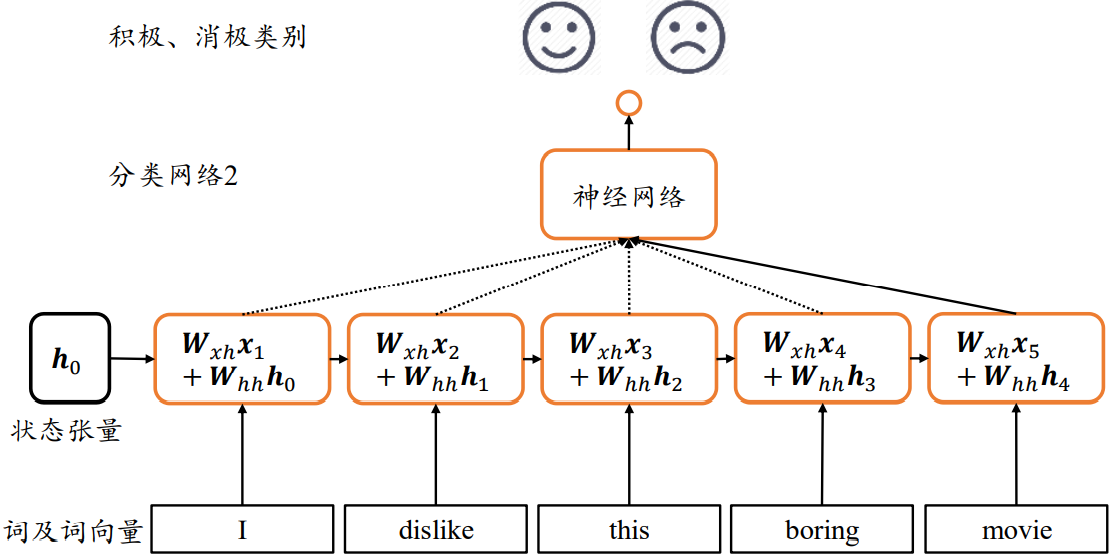
循环神经网络（未添加偏置）

将上述 Memory 机制实现为一个状态张量，如上所示，除了原来的 $𝑾_{xh}$ 参数共享外，还额外增加了一个 $𝑾_{hh}$ 参数，每个时间戳𝑡上状态张量刷新机制为：

h_{𝑡} = 𝜎(𝑾_{xh}x_t + 𝑾_{hh}h_{𝑡−1} + 𝒃)

其中状态张量 $h_0$ 为初始的内存状态，可以初始化为全0，经过𝑠个词向量的输入后得到网络最终的状态张量 𝑠， 𝑠较好地代表了句子的全局语义信息，基于 𝑠通过某个全连接层分类器即可完成情感分类任务。

4.循环神经网络

进一步抽象，如下所示，在每个时间戳𝑡，网络层接受当前时间戳的输入 $x_𝑡$ 和上一个时间戳的网络状态向量 $h_{𝑡−1}$ ，经过

h_𝑡 = 𝑓_𝜃(h_{𝑡−1},x_𝑡)

变换后得到当前时间戳的新状态向量 $h_𝑡$ ，并写入内存状态中，其中：

𝑓_𝜃：网络的运算逻辑
𝜃：网络参数集

在每个时间戳上，网络层均有输出产生 $𝒐_𝑡$ ，𝒐_𝑡 = 𝑔_𝜙(h_𝑡)，即将网络的状态向量变换后输出

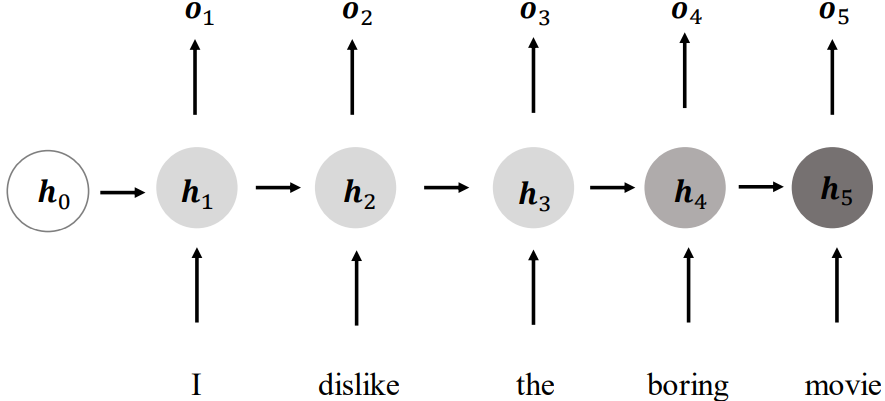
展开的RNN模型

上述网络结构在时间戳上折叠，网络循环接受序列的每个特征向量 $𝒙_t$ ，并刷新内部状态向量 $h_𝑡$ ，同时形成输出 $𝒐_t$ 。对于这种网络结构，称为循环网络结构(Recurrent Neural Network，简称 RNN)：

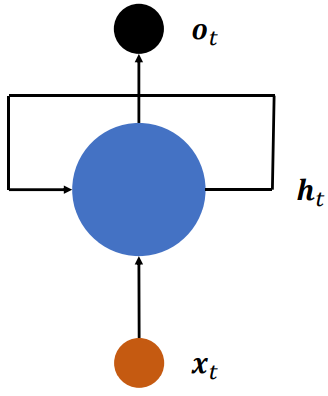
折叠的RNN模型

更特别地，如果使用张量 $𝑾_{xh}$ 、 $𝑾_{hh}$ 和偏置𝒃来参数化𝑓_𝜃网络，并按照

h_𝑡 = 𝜎(𝑾_{xh}x_𝑡 + 𝑾_{hh}h_{𝑡−1} + 𝒃)

方式更新内存状态，我们把这种网络叫做基本的循环神经网络，如无特别说明，一般说的循环神经网络即指这种实现。

在循环神经网络中，激活函数更多地采用 tanh 函数，并且可以选择不使用偏执𝒃来进一步减少参数量。状态向量 $h_𝑡$ 可以直接用作输出，即 $𝒐_𝑡 = h_𝑡$ ，也可以对 $h_𝑡$ 做一个简单的线性变换 $𝒐_𝑡 = 𝑊_{ho}h_𝑡$ 后得到每个时间戳上的网络输出 $𝒐_𝑡$

3、梯度传播

通过循环神经网络的更新表达式可以看出输出对张量 $𝑾_{xh}$ 、 $𝑾_{hh}$ 和偏置𝒃均是可导的，可以利用自动梯度算法来求解网络的梯度。

需要注意的是在推导 \frac{𝜕ℒ}{𝜕𝑾_{ℎℎ}}的过程中发现，\frac{𝜕h_𝑡}{𝜕h_𝑖} 的梯度包含了 $𝑾_{hh}$ 的连乘运算，这是导致循环神经网络训练困难的根本原因

4、RNN层使用方法

在 TensorFlow 中，可以通过 layers.SimpleRNNCell 来完成𝜎(𝑾_{xh}x_𝑡 + 𝑾_{hh}h_{𝑡−1} + 𝒃)计算。

需要注意的是，在 TensorFlow 中，RNN 表示通用意义上的循环神经网络，对于我们目前介绍的基础循环神经网络，它一般叫做 SimpleRNN。

SimpleRNN 与 SimpleRNNCell 的区别：

SimpleRNNCell层：仅仅完成了一个时间戳的前向运算
SimpleRNN层：一般是基于 Cell 层实现的，在内部已经完成了多个时间戳的循环运算

1.SimpleRNNCell

cell = layers.SimpleRNNCell(3) # 创建 RNN Cell，内存向量h长度为 3
cell.build(input_shape=(None,4)) # 输出特征长度 n=4
cell.trainable_variables # 打印 wxh, whh, b 张量

[<tf.Variable 'kernel:0' shape=(4, 3) dtype=float32, numpy=…>,
<tf.Variable 'recurrent_kernel:0' shape=(3, 3) dtype=float32, numpy=…>,
<tf.Variable 'bias:0' shape=(3,) dtype=float32, numpy=array([0., 0., 0.], 
dtype=float32)>]

SimpleRNNCell 内部维护了 3 个张量：

kernel： $𝑾_{xh}$ 张量
recurrent_kernel： $𝑾_{hh}$ 张量
bias：偏置𝒃向量

但是 RNN 的 Memory 向量 $h$ 需要用户自行初始化并记录每个时间戳上的 $h_t$

通过调用 Cell 实例即可完成前向运算：

$𝒐_𝑡,[h_𝑡] = Cell(x_𝑡,[h_{𝑡−1}])$

对于 SimpleRNNCell 来说：

$𝒐_𝑡 = h_𝑡$ ，并没有经过额外的线性层转换，是同一个对象
$h_t$ 通过一个 List 包裹起来，是为了与 LSTM、GRU 等 RNN 变种格式统一。
在循环神经网络的初始化阶段，状态向量 $h_0$ 一般初始化为全 0 向量

例子：

# 初始化状态向量，用列表包裹，统一格式
h0 = [tf.zeros([4, 64])]
x = tf.random.normal([4, 80, 100]) # 生成输入张量[b,s,n]，4 个 80 单词的句子
xt = x[:,0,:] # 所有句子的第 1 个单词

# 构建输入特征 n=100,序列长度 s=80,状态长度=64 的 Cell
cell = layers.SimpleRNNCell(64)
out, h1 = cell(xt, h0) # 前向计算
print(out.shape, h1[0].shape)
(4, 64) (4, 64) # 两者shape一致
print(id(out), id(h1[0])) 
2154936585256 2154936585256 # 两者 id 一致，即状态向量直接作为输出向量

# 对于长度为𝑠的序列来说，需要循环通过 Cell 类𝑠次才算完成一次网络层的前向运算
h = h0 # h 保存每个时间戳上的状态向量列表
# 在序列长度的维度解开输入，得到 xt:[b,n]
for xt in tf.unstack(x, axis=1):
 out, h = cell(xt, h) # 前向计算,out 和 h 均被覆盖
# 最终输出可以聚合每个时间戳上的输出，也可以只取最后时间戳的输出
out = out

2.多层SimpleRNNCell网络

和卷积神经网络动辄几十、上百的深度层数来比，循环神经网络很容易出现梯度弥散和梯度爆炸到现象，深层的循环神经网络训练起来非常困难，目前常见的循环神经网络模型层数一般控制在十层以内。

2层SimpleRNNCell网络例子：

x = tf.random.normal([4,80,100])
xt = x[:,0,:] # 取第一个时间戳的输入 x0
# 构建 2 个 Cell,先 cell0,后 cell1，内存状态向量长度都为 64
cell0 = layers.SimpleRNNCell(64)
cell1 = layers.SimpleRNNCell(64)
h0 = [tf.zeros([4,64])] # cell0 的初始状态向量
h1 = [tf.zeros([4,64])] # cell1 的初始状态向量

# 方式1：先完成一个时间戳上的输入在所有层上的传播，再循环计算完所有时间戳上的输入
for xt in tf.unstack(x, axis=1):
    # xt 作为输入，输出为 out0
    out0, h0 = cell0(xt, h0)
    # 上一个 cell 的输出 out0 作为本 cell 的输入
    out1, h1 = cell1(out0, h1)

# 方式2：先完成输入在第一层上所有时间戳的计算，并保存第一层在所有时间戳上的输出列表，再计算第二层、第三层等的传播
# 保存上一层的所有时间戳上面的输出
middle_sequences = []
# 计算第一层的所有时间戳上的输出，并保存
for xt in tf.unstack(x, axis=1):
    out0, h0 = cell0(xt, h0)
    middle_sequences.append(out0)
# 计算第二层的所有时间戳上的输出
# 如果不是末层，需要保存所有时间戳上面的输出
for xt in middle_sequences:
    out1, h1 = cell1(xt, h1)

一般来说，最末层 Cell 的状态有可能保存了高层的全局语义特征，因此一般使用最末层的输出作为后续任务网络的输入。

更特别地，每层最后一个时间戳上的状态输出包含了整个序列的全局信息，如果只希望选用一个状态变量来完成后续任务，比如情感分类问题，一般选用最末层、最末时间戳的状态输出最为合适。

3.SimpleRNN层

如单层循环神经网络的前向运算：

layer = layers.SimpleRNN(64) # 创建状态向量长度为 64 的 SimpleRNN 层
x = tf.random.normal([4, 80, 100])
out = layer(x) # 和普通卷积网络一样，一行代码即可获得输出（默认返回最后一个时间戳上的输出）
out.shape

TensorShape([4, 64])

如果希望返回所有时间戳上的输出列表，可以设置 return_sequences=True 参数

# 创建 RNN 层时，设置返回所有时间戳上的输出
layer = layers.SimpleRNN(64,return_sequences=True)
out = layer(x) # 前向计算
out # 输出，自动进行了 concat 操作

<tf.Tensor: id=12654, shape=(4, 80, 64), dtype=float32, numpy=
array([[[ 0.31804922, 0.7904409 , 0.13204293, ..., 0.02601025,
 -0.7833339 , 0.65577114],…>

中间维度的 80 即为时间戳维度

于多层循环神经网络：

net = keras.Sequential([ # 构建 2 层 RNN 网络
    # 除最末层外，都需要返回所有时间戳的输出，用作下一层的输入
    layers.SimpleRNN(64, return_sequences=True),
    layers.SimpleRNN(64),
])
out = net(x) # 前向计算

5、RNN感情分类问题实战

待补充

函数	比较逻辑
tf.equal(a, b)	$a=b$
tf.math.greater(a, b)	$a>b$
tf.math.less(a, b)	$a<b$
tf.math.greater_equal(a, b)	$a\geqslant b$
tf.math.less_equal(a, b)	$a\leqslant b$
tf.math.not_equal(a, b)	$a\neq b$
tf.math.is_nan(a, b)	$a=nan$