一、复杂度

时间复杂度

  • nn 表示数据规模
  • O(f(n))O(f(n)) 表示运行算法所需要执行的指令数，和 f(n)f(n) 成正比。

在学术界，严格地讲， O(f(n))O(f(n)) 表示算法执行的上界，如：归并排序算法的时间复杂度是 O(nlogn)O(nlogn) 的，同时也是 O(n2)O(n^2)

在业界，则使用 OO 来表示算法执行的最低上界，所以一般不会说归并排序是 O(n2)O(n^2) 的

例子：

有一个字符串数组，将数组中的每一个字符串按照字母序排序；之后再将整个字符串数组按照字典序排序。整个操作的时间复杂度？

假设最长的字符串长度为s；数组中有n个字符串

  • 对每个字符串排序：O(slogs)O(slogs)
  • 将数组中的每一个字符串按照字母序排序：O(n∗slog(s))O(n*slog(s))
  • 将整个字符串数组按照字典序排序：O(s∗nlog(n))O(s*nlog(n)) （n个字符串，比较nlognnlogn次，每次都是字符串比较，最坏需要比较s次）
  • 结果：O(n∗slog(s))+O(s∗nlog(n))=O(n∗s∗logs+s∗n∗logn)=O(n∗s∗(logs+logn))O(n*slog(s))+O(s*nlog(n))=O(n*s*logs+s*n*logn)=O(n*s*(logs+logn))

C++中常见数据结构时间复杂度：

数据结构 时间复杂度
vector push_back/pop_back为O(1)O(1)
insert/erase为O(n)O(n)
list（双向链表） push_front/push_back/pop_front/pop_back/insert/erase均为O(1)O(1)
deque push_front/push_back/pop_front/pop_back均为O(1)O(1)
insert/erase均为O(n)O(n)
set/multiset（红黑树） 增删改查近似O(logN)O(logN)
map/multimap（红黑树） 增删改查近似O(logN)O(logN)
unordered_set/unordered_map（哈希表） 查找的时间复杂度可达到O(1)O(1)，但是需要格外空间保存哈希表
prioroty_queue（默认最大堆） push/pop为O(logN)O(logN)

技巧：

  • n经过几次"除以x"操作后等于1 ==> logxnlog_xn ==> O(logn)O(logn) （log函数定义），如：二分查找

  • 如果递归函数中，只进行一次递归调用，递归深度为depth；在每个递归函数中，时间复杂度为T；则总体的时间复杂度为O(T∗depth)O(T*depth)。如：二分查找为O(logn)O(logn)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    // 递归深度为logn ==> O(logn)
    double pow( double x, int n )
    {
        assert( n>=0 );
        if( n==0 )
            return 1.0;
        double t= pow(x, n/2);
        if( n%2 )
            return x*t*t:
        return t*t:
    }

  • 如果递归函数中，只进行多次递归调用时需要画出递归树来求出递归的次数，主要就是该次数决定最终的复杂度

空间复杂度

  • 多开一个辅助的数组：O(n)O(n)
  • 多开一个辅助的二维数组：O(n2)O(n^2)
  • 多开常数空间：O(1)O(1)

二、数组

二分查找

写出正确程序的思路：

  1. 明确变量的含义：每个变量都需要有清晰的定义（左边界l和右边界r在程序一开始的定义即可，之后只需根据该定义来编写程序即可）
  2. 循环不变量：由上述变量产生一个概念——循环不变量，在循环中改变这些变量的取值并不代编改变他们的定义，需要一直在循环中维护他们的含义
  3. 小数据量调试：注意边界等特殊情况（如NULL、不在数据集等）

[l...r]的范围：

1
2
3
4
5
6
7
8
9
10
11
12
13
template<typename T>
int binarySearch(T arr[], int n, T target){
    int l = 0, r = n - 1; // 在[l...r]的范围里寻找target
    while(l <= r){    // 当 l == r时,区间[l...r]依然是有效的
        int mid = l + (r - l) / 2;
        if(arr[mid] == target) return mid;
        if(target > arr[mid])
            l = mid + 1;  // target在[mid+1...r]中; [l...mid]一定没有target
        else    // target < arr[mid]
            r = mid - 1;  // target在[l...mid-1]中; [mid...r]一定没有target
    }
    return -1;
}

[l...r)的范围：

1
2
3
4
5
6
7
8
9
10
11
12
13
template<typename T>
int binarySearch(T arr[], int n, T target){
    int l = 0, r = n; // target在[l...r)的范围里
    while(l < r){    // 当 l == r 时, 区间[l...r)是一个无效区间
        int mid = l + (r - l) / 2;
        if(arr[mid] == target) return mid;
        if(target > arr[mid])
            l = mid + 1;    // target在[mid+1...r)中; [l...mid]一定没有target
        else// target < arr[mid]
            r = mid;        // target在[l...mid)中; [mid...r)一定没有target
    }
    return -1;
}

例题详见[对撞指针](# 对撞指针)、[滑动窗口](# 滑动窗口)

移动数组元素

283. 移动零：给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

1
2
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

说明:

  1. 必须在原数组上操作，不能拷贝额外的数组。
  2. 尽量减少操作次数。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 原地(in place)解决该问题
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
    void moveZeroes(vector<int>& nums) {

        int k = 0; // nums中, [0...k)的元素均为非0元素

        // 遍历到第i个元素后,保证[0...i]中所有非0元素
        // 都按照顺序排列在[0...k)中
        // 同时, [k...i] 为 0
        for(int i = 0 ; i < nums.size() ; i ++)
            if(nums[i])
                if(k != i)
                    swap(nums[k++] , nums[i]);
                else
                    k ++;
    }
};

相似题目：27. 移除元素、26. 删除排序数组中的重复项、80. 删除排序数组中的重复项 II

三路快排

75. 颜色分类：给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

示例 1：

1
2
输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]

示例 2：

1
2
输入：nums = [2,0,1]
输出：[0,1,2]

示例 3：

1
2
输入：nums = [0]
输出：[0]

示例 4：

1
2
输入：nums = [1]
输出：[1]

提示：

  • n == nums.length
  • 1 <= n <= 300
  • nums[i] 为 0、1 或 2

进阶：

  • 你可以不使用代码库中的排序函数来解决这道题吗？
  • 你能想出一个仅使用常数空间的一趟扫描算法吗？

实现：

计数排序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 计数排序的思路
// 对整个数组遍历了两遍
// 时间复杂度: O(n)
// 空间复杂度: O(k), k为元素的取值范围
class Solution {
public:
    void sortColors(vector<int> &nums) {
        int count[3] = {0};    // 存放0, 1, 2三个元素的频率
        for(int i = 0 ; i < nums.size() ; i ++){
            assert(nums[i] >= 0 && nums[i] <= 2);
            count[nums[i]] ++;
        }

        int index = 0;
        for(int i = 0 ; i < count[0] ; i ++)
            nums[index++] = 0;
        for(int i = 0 ; i < count[1] ; i ++)
            nums[index++] = 1;
        for(int i = 0 ; i < count[2] ; i ++)
            nums[index++] = 2;
    }
};

三路快排：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 三路快速排序的思想
// 对整个数组只遍历了一遍
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
    void sortColors(vector<int> &nums) {
        int zero = -1;          // [0...zero] == 0
        int two = nums.size();  // [two...n-1] == 2
        for(int i = 0 ; i < two ; ){
            if(nums[i] == 1)
                i++;
            else if (nums[i] == 2)
                swap( nums[i] , nums[--two]);
            else{ // nums[i] == 0
                assert(nums[i] == 0);
                swap(nums[++zero] , nums[i++]);
            }
        }
    }
};

相似题目：88. 合并两个有序数组、215. 数组中的第K个最大元素

对撞指针

167. 两数之和 II - 输入有序数组：给定一个已按照 升序排列 的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。

函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ，所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。

你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

示例 1：

1
2
3
输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

示例 2：

1
2
输入：numbers = [2,3,4], target = 6
输出：[1,3]

示例 3：

1
2
输入：numbers = [-1,0], target = -1
输出：[1,2]

提示：

  • 2 <= numbers.length <= 3 * 104
  • -1000 <= numbers[i] <= 1000
  • numbers 按 递增顺序 排列
  • -1000 <= target <= 1000
  • 仅存在一个有效答案

实现：

二分查找：

  1. 遍历数组，设当前遍历元素序号为i，时间复杂度O(n)O(n)
  2. 在(i,end]之间通过二分搜索来查找元素target-nums[i]，时间复杂度O(logn)O(logn)
  3. 总体时间复杂度为O(nlogn)O(nlogn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// 二分搜索法
// 时间复杂度: O(nlogn)
// 空间复杂度: O(1)
class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        assert(numbers.size() >= 2);
        // assert(isSorted(numbers));

        for(int i = 0 ; i < numbers.size() - 1 ; i ++){
            int j = binarySearch(numbers, i+1, numbers.size()-1, target - numbers[i]);
            if(j != -1){
                int res[2] = {i+1, j+1};
                return vector<int>(res, res+2);
            }
        }

        throw invalid_argument("the input has no solution");
    }

private:
    int binarySearch(const vector<int> &nums, int l, int r, int target){
        assert(l >= 0 && l < nums.size());
        assert(r >= 0 && r < nums.size());

        while(l <= r){
            int mid = l + (r - l)/2;
            if(nums[mid] == target)
                return mid;
            if(target > nums[mid])
                l = mid + 1;
            else
                r = mid - 1;
        }

        return -1;
    }

    bool isSorted(const vector<int>& numbers){
        for(int i = 1 ; i < numbers.size() ; i ++)
            if(numbers[i] < numbers[i-1])
                return false;
        return true;
    }
};

对撞指针：两个指针向相对的方向前进，这个过程中就可能找到需要求解问题的答案

思路：

对撞指针

选定初始i、j为数组首和尾，此时对于nums[i]+nums[j]和target的大小无外乎以下几种：

  1. nums[i]+nums[j]<target：增加索引i
  2. nums[i]+nums[j]>target：减小索引j
  3. nums[i]+nums[j]==target：刚好找到

重复上述步骤，缩小索引i和j的范围直至找到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 对撞指针
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        assert(numbers.size() >= 2);
        // assert(isSorted(numbers));

        int l = 0, r = numbers.size() - 1;
        while(l < r){
            if(numbers[l] + numbers[r] == target){
                int res[2] = {l+1, r+1};
                return vector<int>(res, res+2);
            }
            else if(numbers[l] + numbers[r] < target)
                l ++;
            else // numbers[l] + numbers[r] > target
                r --;
        }

        throw invalid_argument("the input has no solution");
    }

private:
    bool isSorted(const vector<int>& numbers){
        for(int i = 1 ; i < numbers.size() ; i ++)
            if(numbers[i] < numbers[i-1])
                return false;
        return true;
    }
};

相似题目：125. 验证回文串、344. 反转字符串、345. 反转字符串中的元音字母、11. 盛最多水的容器

滑动窗口

209. 长度最小的子数组：给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

1
2
3
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

1
2
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

1
2
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

  • 1<=target<=1091 <= target <= 10^9
  • 1<=nums.length<=1051 <= nums.length <= 10^5
  • 1<=nums[i]<=1051 <= nums[i] <= 10^5

进阶：

如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

实现：

滑动窗口

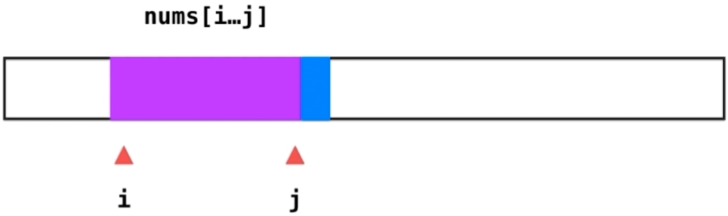
  • 假设一个连续子数组从i到j，此时nums[i…j]的和小于目标s
  • 此时j++，增加窗口长度，再观察其总和与s的大小。直至其总和>s，记录此时子数组长度
  • 缩小i，即i++，直至某时刻其总和<s
  • 重复上述步骤直至整个数组遍历完毕
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 滑动窗口的思路
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        assert(s > 0);

        int l = 0 , r = -1; // nums[l...r]为我们的滑动窗口
        int sum = 0;
        int res = nums.size() + 1;

        while(l < nums.size()){   // 窗口的左边界在数组范围内,则循环继续
            if(r + 1 < nums.size() && sum < s)//右边界+1后仍在数组中，且此时子数组总和<s
                sum += nums[++r];
            else // r已经到头 或者 sum >= s
                sum -= nums[l++];

            if(sum >= s)//总和大于预期目标s
                res = min(res, r - l + 1);
        }

        if(res == nums.size() + 1)//排除无解情况
            return 0;
        return res;
    }
};

二分搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 扩展暴力解法的方法。对于每一个l, 可以使用二分搜索法搜索r
//
// 时间复杂度: O(nlogn)
// 空间复杂度: O(n)
class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        assert(s > 0);

        // sums[i]存放nums[0...i-1]的和
        vector<int> sums(nums.size() + 1, 0);
        for(int i = 1 ; i <= nums.size() ; i ++)
            sums[i] = sums[i-1] + nums[i-1];

        int res = nums.size() + 1;
        for(int l = 0 ; l < (int)nums.size(); l ++){
            auto r_bound = lower_bound(sums.begin(), sums.end(), sums[l] + s);
            if(r_bound != sums.end()){
                int r = r_bound - sums.begin();
                res = min(res, r - l);
            }
        }

        if(res == nums.size() + 1)
            return 0;

        return res;
    }
};

3. 无重复字符的最长子串：给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

1
2
3
输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

1
2
3
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

1
2
3
4
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

示例 4:

1
2
输入: s = ""
输出: 0

提示：

  • 0<=s.length<=5∗1040 <= s.length <= 5 * 10^4
  • s 由英文字母、数字、符号和空格组成

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 滑动窗口
// 时间复杂度: O(len(s))
// 空间复杂度: O(len(charset))
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int freq[256] = {0};//题中为ascii字符，用一个数组记录窗口中出现的频率，提高查找效率

        int l = 0, r = -1; //滑动窗口为s[l...r]
        int res = 0;

        // 整个循环从 l == 0; r == -1 这个空窗口开始
        // 到l == s.size(); r == s.size()-1 这个空窗口截止
        // 在每次循环里逐渐改变窗口, 维护freq, 并记录当前窗口中是否找到了一个新的最优值
        while(l < s.size()){
            if(r + 1 < s.size() && freq[s[r+1]] == 0)//保证r+1号元素不越界
                freq[s[++r]] ++;
            else    //r已经到头 || freq[s[r+1]] == 1 此时逐渐缩小左边界
                freq[s[l++]] --;

            res = max(res, r-l+1);
        }

        return res;
    }
};

相似题目：438. 找到字符串中所有字母异位词、76. 最小覆盖子串

总结与感悟

  1. 注意边界

  2. 字符串在比较的过程中一定要注意字符集的关系，如：是否需要区分大小写、是否有数字、是否是ASCII等，一般会用到判断：isdigit()，islower()，isupper()，isalpha()，isalnum()，转换：toupper()，tolower()

  3. 大小写的一个转化方法（注意加上小括号，位运算优先级比较低）：

    1. 统一转成大写：ch & 0b11011111 简写：ch & 0xDF
    2. 统一转成小写：ch | 0b00100000 简写：ch | 0x20

  4. 滑动窗口需要注意扩大右侧边界的条件与缩小左侧边界的条件，一般来说是由同一个变量导致的。若是字符串， 需要考虑是否应该通过一个字符表来记录

  5. 一般在排序的数组（或者部分排序的数组）中查找一个数字或统计某个数字出现的次数，可以尝试用二分查找（如旋转数组找最小值、旋转数组找目标值）

  6. 在快排的partition中，待比较数据v的选择通过随机方法选择，一般通过如下：

    1
    2
    srand(time(0));
    int randm = rand()%(end-start+1)+start;
    • 注意end-start+1，+1是为了防止end-start==0的情况发生，同时也能够避免选取的元素刚好就是数组最前面的元素

  7. cin效率低可以通过使用std::ios::sync_with_stdio(false);解决，使其基本可以和scanf进行比较

  8. string中常用的方法：

    • front/back：查看，返回首尾的引用

    • pop_back/push_back/insert：插入删除

    • stoi/stol/stoll/stod/stold/stof：string转数字

    • atoi：const char *转int，C语言函数，头文件stdlib.h中

    • c_str：string转const char *，如需修改，需要借助std::strcpy (cstr, str.c_str());改变类型

    • substr：

      1
      string substr(size_t pos = 0, size_t len = npos) const;
      • 返回一个string，包含s中从pos开始的n个字符的拷贝（pos的默认值是0，n的默认值是s.size() - pos，即不加参数会默认拷贝整个s）
      • 若pos的值超过了string的大小，则substr函数会抛出一个out_of_range异常；若pos+n的值超过了string的大小，则substr会调整n的值，只拷贝到string的末尾

    • find_first_not_of/find_last_not_of：

      1
      2
      3
      4
      size_type find_first_not_of( const basic_string &str, size_type index = 0 );
      size_type find_first_not_of( const char *str, size_type index = 0 );
      size_type find_first_not_of( const char *str, size_type index, size_type num );
      size_type find_first_not_of( char ch, size_type index = 0 );
      • 在字符串中查找第一个与str/ch中的字符都不匹配的字符，返回它的位置。搜索从index开始，最多查找num个字符。如果没找到就返回string::nops

    • find_first_of/find_last_of：与上述一致，只是查找的是第一个匹配的字符串

    • find：string中的find与上述find_first_of一致

    • 去除两端空格trim：主要为find_first_not_of和find_last_not_of方法

      1
      2
      3
      4
      5
      string trim(const string str)
      {
          string tmp = str.substr(str.find_first_not_of(" "));
          return tmp.substr(0,tmp.find_last_not_of(" ")+1);
      }

    • 字符串分割split：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      std::vector<std::string> split(const std::string &s, char delim)
      {
          std::vector<std::string> elems;
          std::stringstream ss(s);
          std::string item;
          while (std::getline(ss, item, delim)) {
              elems.push_back(item);
          }
          return elems;
      }

  9. deque：

    • front/back：查看，返回首尾的引用
    • push_front/push_back/pop_front/pop_back/insert/emplace：插入删除
    • emplace_front/emplace_back：推荐替代push_front/push_back

  10. list：

  • front/back：查看，返回首尾的引用
  • push_front/push_back/pop_front/pop_back/insert/emplace：插入删除
  • emplace_front/emplace_back：推荐替代push_front/push_back

  1. stack：

    • top：查看栈顶元素的引用
    • push/emplace/pop：插入弹出

  2. queue：

    • front/back：查看，返回首尾的引用
    • push/emplace/pop：插入弹出

三、查找表

一般有两种问题：

  1. 查找有无：元素’a’是否存在？一般用set集合
  2. 查找对应关系：元素’a’出现了几次？一般用map字典（c++中map如果没有对应的键值对，但是只要一访问，就会将访问的键所对应的默认值设为0，且需要通过map.erase()才能真正删除该键值对）

c++中set和map背后都是一个平衡的二分搜索树，对于元素的插入、查找、删除的时间复杂度均为O(logn)O(logn)

c++中unordered_set和unordered_map背后都是一个哈希表，对于元素的插入、查找、删除的时间复杂度均为O(1)O(1)，但是由于哈希表的特性，会失去数据的顺序性，即以下特性会丢失：

  • 数据集中的最大值和最小值
  • 某个元素的前驱和后继
  • 某个元素的floor和ceil（c++中只有ceil的实现：lower_bound(x)，查找不小于目标值的第一个元素并返回对应的迭代器，即查找一个**>=x的元素；对应的upper_bound(x)为查找一个>**x的元素）
  • 某个元素的排位rank
  • 选择某个排位的元素 select

set和map的常见操作：

  • insert
  • find
  • erase
  • change（仅仅map，改变键所对应的值）

set和map基本使用

349. 两个数组的交集：给定两个数组，编写一个函数来计算它们的交集。

示例 1：

1
2
输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

示例 2：

1
2
输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]

说明：

  • 输出结果中的每个元素一定是唯一的。
  • 我们可以不考虑输出结果的顺序。

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 时间复杂度: O(nlogn)
// 空间复杂度: O(n)
class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        set<int> record(nums1.begin(), nums1.end());

        set<int> resultSet;
        for( int i = 0 ; i < nums2.size() ; i ++ )
            if( record.find(nums2[i]) != record.end() )//set查找
                resultSet.insert( nums2[i] );//set插入

        return vector<int>(resultSet.begin(), resultSet.end());
    }
};
  • 可以完成替换成unordered_set，加快查找与插入，整个算法的时间复杂度会变为O(n)O(n)

350. 两个数组的交集 II：给定两个数组，编写一个函数来计算它们的交集。

示例 1：

1
2
输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]

示例 2:

1
2
输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[4,9]

说明：

  • 输出结果中每个元素出现的次数，应与元素在两个数组中出现次数的最小值一致。
  • 我们可以不考虑输出结果的顺序。

进阶：

  • 如果给定的数组已经排好序呢？你将如何优化你的算法？
  • 如果 nums1 的大小比 nums2 小很多，哪种方法更优？
  • 如果 nums2 的元素存储在磁盘上，内存是有限的，并且你不能一次加载所有的元素到内存中，你该怎么办？

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 时间复杂度: O(nlogn)
// 空间复杂度: O(n)
class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {

        map<int, int> record;
        for(int i = 0 ; i < nums1.size() ; i ++)
            record[nums1[i]] += 1;

        vector<int> resultVector;
        for(int i = 0 ; i < nums2.size() ; i ++)
            if(record[nums2[i]] > 0){
                resultVector.push_back(nums2[i]);
                record[nums2[i]] --;
            }

        return resultVector;
    }
};
  • 注意map一旦访问即会产生默认键值对
  • 可以完全替换为unordered_map，加快查找与插入，整个算法的时间复杂度会变为O(n)O(n)

相似题目：242. 有效的字母异位词、202. 快乐数、290. 单词规律、205. 同构字符串、451. 根据字符出现频率排序

经典问题

1. 两数之和：给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

你可以按任意顺序返回答案。

示例 1：

1
2
3
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

1
2
输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

1
2
输入：nums = [3,3], target = 6
输出：[0,1]

提示：

  • 2<=nums.length<=1032 <= nums.length <= 10^3
  • −109<=nums[i]<=109-10^9 <= nums[i] <= 10^9
  • −109<=target<=109-10^9 <= target <= 10^9
  • 只会存在一个有效答案

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 时间复杂度：O(n)
// 空间复杂度：O(n)
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> record;//查找表，key：数组中的值，val：对应的索引
        for(int i = 0 ; i < nums.size() ; i ++){

            int complement = target - nums[i];//要查找的值
            if(record.find(complement) != record.end()){// 尝试查找 时间复杂度O(1)
                int res[] = {i, record[complement]};
                return vector<int>(res, res + 2);
            }

            record[nums[i]] = i;//记录键值对
        }
        throw invalid_argument("the input has no solution");
    }
};
  • 这里由于传入数组中可能存在重复的值，所以不是直接将所有数组中的值一次性存入map中
  • 在遍历时，仅仅只查找之前已经遍历过的元素即可：
    • 对于重复元素，之前记录的查找表中肯定存在，不管重复几次，总之是有输出（题目要求只会有唯一解）

相似题目：15. 三数之和、18. 四数之和、16. 最接近的三数之和

灵活选择键值

454. 四数相加 II：给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ，使得 A[i] + B[j] + C[k] + D[l] = 0。

为了使问题简单化，所有的 A, B, C, D 具有相同的长度 N，且 0 ≤ N ≤ 500 。所有整数的范围在 −228-2^{28} 到 228−12^{28} - 1 之间，最终结果不会超过 231−12^{31} - 1 。

例如:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入:
A = [ 1, 2]
B = [-2,-1]
C = [-1, 2]
D = [ 0, 2]

输出:
2

解释:
两个元组如下:

1. (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 时间复杂度: O(n^2)
// 空间复杂度: O(n^2)
class Solution {
public:
    int fourSumCount(vector<int>& A, vector<int>& B, vector<int>& C, vector<int>& D) {
        unordered_map<int,int> hashtable;
        for(int i = 0 ; i < C.size() ; i ++)
            for(int j = 0 ; j < D.size() ; j ++)
                hashtable[C[i]+D[j]] += 1;//选择将C+D的和存入查找表中，将暴力解法的时间复杂度由O(n^4)-->O(n^2)，降低到可以接受的程度

        int res = 0;
        for(int i = 0 ; i < A.size() ; i ++)
            for(int j = 0 ; j < B.size() ; j ++)
                if(hashtable.find(-A[i]-B[j]) != hashtable.end())
                    res += hashtable[-A[i]-B[j]];

        return res;
    }
};
  • 由于0 ≤ N ≤ 500，所以O(n3)O(n^3)可能会超时，而O(n2)O(n^2)不会

相似题目：49. 字母异位词分组

447. 回旋镖的数量：给定平面上 n 对 互不相同 的点 points ，其中 points[i] = [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ，其中 i 和 j 之间的距离和 i 和 k 之间的距离相等（需要考虑元组的顺序）。

返回平面上所有回旋镖的数量。

示例 1：

1
2
3
输入：points = [[0,0],[1,0],[2,0]]
输出：2
解释：两个回旋镖为 [[1,0],[0,0],[2,0]] 和 [[1,0],[2,0],[0,0]]

示例 2：

1
2
输入：points = [[1,1],[2,2],[3,3]]
输出：2

示例 3：

1
2
输入：points = [[1,1]]
输出：0

提示：

  • n == points.length
  • 1 <= n <= 500
  • points[i].length == 2
  • −104<=xi,yi<=104-10^4 <= x_i, y_i <= 10^4
  • 所有点都 互不相同

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 时间复杂度: O(n^2)
// 空间复杂度: O(n)
class Solution {
public:
    int numberOfBoomerangs(vector<pair<int, int>>& points) {
        int res = 0;
        for( int i = 0 ; i < points.size() ; i ++ ){
            // record中存储 点i 到 所有其他点的距离 出现的频次
            unordered_map<int, int> record;
            for(int j = 0 ; j < points.size() ; j ++)
                if(j != i)
                    // 计算距离时不进行开根运算, 以防止产生小数
                    record[dis(points[i], points[j])] += 1;

            for(unordered_map<int, int>::iterator iter = record.begin() ; iter != record.end() ; iter ++)//迭代器遍历unordered_map
                res += (iter->second) * (iter->second - 1);
        }
        return res;
    }

private:
    int dis(const pair<int,int> &pa, const pair<int,int> &pb){
        return (pa.first - pb.first) * (pa.first - pb.first) +
               (pa.second - pb.second) * (pa.second - pb.second);
    }
};

相似题目：149. 直线上最多的点数

滑动窗口+查找表

219. 存在重复元素 II：给定一个整数数组和一个整数 k，判断数组中是否存在两个不同的索引 i 和 j，使得 nums [i] = nums [j]，并且 i 和 j 的差的 绝对值 至多为 k。

示例 1:

1
2
输入: nums = [1,2,3,1], k = 3
输出: true

示例 2:

1
2
输入: nums = [1,0,1,1], k = 1
输出: true

示例 3:

1
2
输入: nums = [1,2,3,1,2,3], k = 2
输出: false

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 时间复杂度: O(n)
// 空间复杂度: O(k)
class Solution {
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) {
        if(nums.size() <= 1)
            return false;
        if(k <= 0)
            return false;

        unordered_set<int> record;
        for(int i = 0 ; i < nums.size() ; i ++){

            if(record.find(nums[i]) != record.end())
                return true;

            record.insert(nums[i]);

            // 保持record中最多有k个元素
            // 因为在下一次循环中会添加一个新元素,使得总共考虑k+1个元素
            if(record.size() == k + 1)
                record.erase(nums[i - k]);
        }
        return false;
    }
};

相似题目：217. 存在重复元素

220. 存在重复元素 III：在整数数组 nums 中，是否存在两个下标 i 和 j，使得 nums [i] 和 nums [j] 的差的绝对值小于等于 t ，且满足 i 和 j 的差的绝对值也小于等于 ķ 。

如果存在则返回 true，不存在返回 false。

示例 1:

1
2
输入: nums = [1,2,3,1], k = 3, t = 0
输出: true

示例 2:

1
2
输入: nums = [1,0,1,1], k = 1, t = 2
输出: true

示例 3:

1
2
输入: nums = [1,5,9,1,5,9], k = 2, t = 3
输出: false

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 时间复杂度: O(nlogk)
// 空间复杂度: O(k)
class Solution {
public:
    bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {

        // 这个问题的测试数据在使用int进行加减运算时会溢出
        // 所以使用long long
        set<long long> record;
        for(int i = 0 ; i < nums.size() ; i ++){
            if(record.lower_bound((long long)nums[i] - (long long)t) != record.end() &&
                *record.lower_bound((long long)nums[i] - (long long)t ) <= (long long)nums[i] + (long long)t)// 存在nums[i]-t且该值不会超过nums[i]+t，即[nums[i]-t,nums[i]+t]中
                return true;

            record.insert(nums[i]);

            if(record.size() == k + 1)
                record.erase( nums[i-k] );
        }

        return false;
    }
};
  • 注意nums[i]+t或nums[i]-t可能会导致整形溢出，所以需要改为long long（测试用例：[-1,2147483647]，k=1，t=2147483647）

总结与感悟

  1. 对于元素的插入、查找、删除的时间复杂度均为O(logn)O(logn)
  2. set是有序的，在某些方面（如：排序、最大值、最小值、去重、判断是否存在时）可以借助set或multiset（相较于set，其中key能重复）

四、链表

基础使用

206. 反转链表：反转一个单链表。

示例:

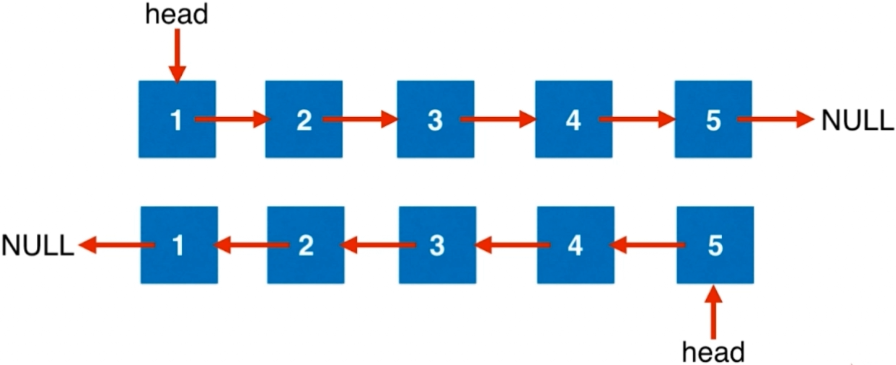
1
2
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

进阶:

  • 你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

注意：一般来说这种题目不能通过一个栈来实现，而是通过操作每个节点的next指针来处理，如下所示：

反转指针

基本思路：

基本思路

  1. 改变cur节点的指针指向pre节点
  2. 更新pre、cur、next三个指针，均往前移动一个位置
  3. 重复上述步骤，直至

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = NULL;
        ListNode* cur = head;
        while(cur != NULL){
            ListNode* next = cur->next;
            cur->next = pre;//反转
            pre = cur;//更新
            cur = next;
        }

        return pre;
    }
};

递归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        // 递归终止条件
        if(head == NULL || head->next == NULL)
            return head;

        ListNode* rhead = reverseList(head->next);

        // head->next此刻指向head后面的链表的尾节点
        // head->next->next = head把head节点放在了尾部
        head->next->next = head;
        head->next = NULL;

        return rhead;
    }
};

相似题目：92. 反转链表 II、83. 删除排序链表中的重复元素、86. 分隔链表、328. 奇偶链表、2. 两数相加、445. 两数相加 II

设立虚拟头结点

203. 移除链表元素：删除链表中等于给定值 val 的所有节点。

示例:

1
2
输入: 1->2->6->3->4->5->6, val = 6
输出: 1->2->3->4->5

思路：

删除节点

  • 该操作对删除最后一个元素仍然适用，但是对第一个元素不适用（删除元素必须为cur的next指针）
  • 可以通过一定手段解决第一个元素的问题，但是需要注意的细节有点多，不推荐

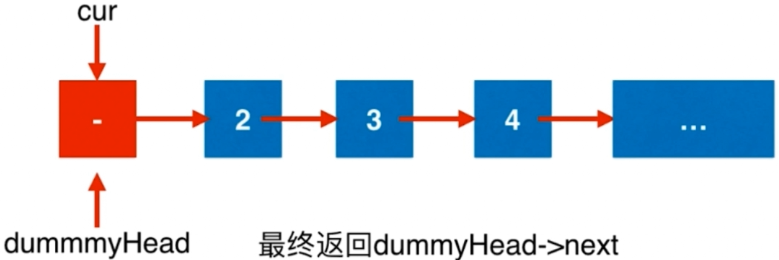
虚拟头节点

  • 通过创建一个虚拟头节点的方式能够很好的解决上述问题，但是最后需要释放掉创建的虚拟头节点

解题：

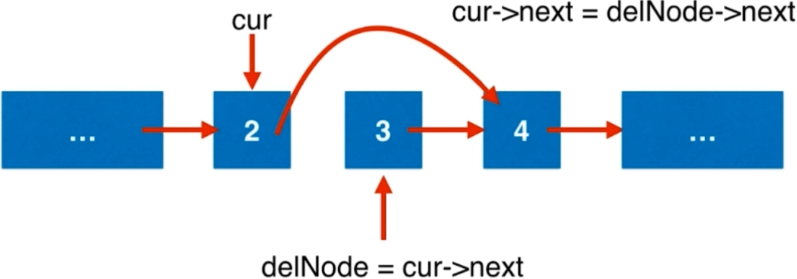
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        // 创建虚拟头结点（节点中的值无所谓）
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;//放在真正的头节点之前
        //删除操作（如果不是虚拟头节点，这一块需要很多铺垫工作解决删除节点是头节点的特例）
        ListNode* cur = dummyHead;
        while(cur->next != NULL){
            if(cur->next->val == val){
                ListNode* delNode = cur->next;
                cur->next = delNode->next;
                delete delNode;
            }
            else
                cur = cur->next;
        }

        ListNode* retNode = dummyHead->next;//获得真正的头节点
        delete dummyHead;//释放内存

        return retNode;
    }
};

相似题目：82. 删除排序链表中的重复元素 II、21. 合并两个有序链表

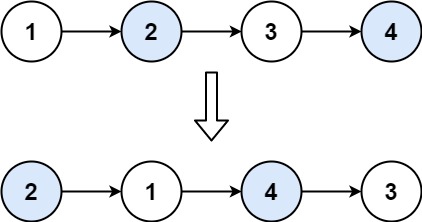
24. 两两交换链表中的节点：给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例 1：

示例1

1
2
输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

1
2
输入：head = []
输出：[]

示例 3：

1
2
输入：head = [1]
输出：[1]

提示：

  • 链表中节点的数目在范围 [0, 100] 内
  • 0 <= Node.val <= 100

进阶：你能在不修改链表节点值的情况下解决这个问题吗?（也就是说，仅修改节点本身。）

思路：

交换节点

  • 设立一个虚拟头节点以及对应的指针p
  • 通过上图中的四个指针交换节点1和节点2
  • 指针p指向下一对节点的前一个节点，即节点2（交换后为节点1）处，再依次更新剩余三个指针，重复上述步骤即可

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0);//创建虚拟头节点
        dummyHead->next = head;//放在真正的头节点之前
        // 真正的swap操作
        ListNode* p = dummyHead;
        while(p->next && p->next->next){
            ListNode* node1 = p->next;
            ListNode* node2 = node1->next;
            ListNode* next = node2->next;
            node2->next = node1;//swap
            node1->next = next;
            p->next = node2;
            p = node1;//更新p指针
        }

        ListNode* retHead = dummyHead->next;//获得真正的头节点
        delete dummyHead;//释放内存

        return retHead;
    }
};

相似题目：25. K 个一组翻转链表、147. 对链表进行插入排序、148. 排序链表（大多数排序均要求随机访问，但是归并排序不需要，尤其是自顶向上的归并排序更容易在链表中实现）

其他情况

237. 删除链表中的节点：请编写一个函数，使其可以删除某个链表中给定的（非末尾）节点。传入函数的唯一参数为 要被删除的节点 。

现有一个链表：head = [4,5,1,9]，它可以表示为:

链表head

示例 1：

1
2
3
输入：head = [4,5,1,9], node = 5
输出：[4,1,9]
解释：给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.

示例 2：

1
2
3
输入：head = [4,5,1,9], node = 1
输出：[4,5,9]
解释：给定你链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9.

提示：

  • 链表至少包含两个节点。
  • 链表中所有节点的值都是唯一的。
  • 给定的节点为非末尾节点并且一定是链表中的一个有效节点。
  • 不要从你的函数中返回任何结果。

思路：在该题目中，无法获取上一个节点，故只能通过修改该节点的值来实现

解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
// 时间复杂度: O(1)
// 空间复杂度: O(1)
class Solution {
public:
    void deleteNode(ListNode* node) {
        // 注意: 这个方法对尾节点不适用。题目中要求了给定的node不是尾节点
        // 在assert中, 我们使用node->next != NULL确保了node不是尾节点
        assert(node != NULL && node->next != NULL);

        node->val = node->next->val;//复制下个节点的值
        ListNode* delNode = node->next;//记住下个节点
        node->next = delNode->next;//跳过下个节点

        delete delNode;//直接删除下个节点

        return;
    }
};

双指针

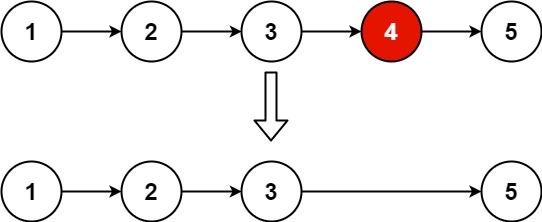
19. 删除链表的倒数第 N 个结点：给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

进阶：你能尝试使用一趟扫描实现吗？

示例 1：

示例1

1
2
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

1
2
输入：head = [1], n = 1
输出：[]

示例 3：

1
2
输入：head = [1,2], n = 1
输出：[1]

提示：

  • 链表中结点的数目为 sz
  • 1 <= sz <= 30
  • 0 <= Node.val <= 100
  • 1 <= n <= sz

思路：

常规思路：

  1. 遍历第一遍，求出链表的总长度
  2. 遍历第二遍，找到倒数第n个节点并删除

优化（仅仅只少遍历一次，时间、空间复杂度仍然是一样的）：

双指针

  1. 假设n=2时，令p为要删除的前一个节点的指针，q为最后一个节点（空节点），此时p和q之间的距离是固定的
  2. 按照上述说明，初始化p为虚拟头指针，q为p后n+1个元素的指针
  3. p和q一直向前移动，直至q到达末尾，此时p的下一个元素即为待删除元素
  4. 整个过程只需要遍历一遍链表即可

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0);//创建虚拟头指针
        dummyHead->next = head;
        // 初始化p、q指针
        ListNode* p = dummyHead;
        ListNode* q = dummyHead;
        for( int i = 0 ; i < n + 1 ; i ++ ){
            assert(q);
            q = q->next;
        }
        //p、q同时向前移动
        while(q){
            p = p->next;
            q = q->next;
        }
        //删除p后节点
        ListNode* delNode = p->next;
        p->next = delNode->next;
        delete delNode;
        //将虚拟头节点删除，还原真正的头节点
        ListNode* retNode = dummyHead->next;
        delete dummyHead;

        return retNode;
    }
};

相似题目：61. 旋转链表、143. 重排链表（找到中间点，切成两部分，后一部分做个倒序，然后连接起来即可。难点在找到中间点。另一种方法是两次遍历，第一次获得总长度）、234. 回文链表

总结与感悟

  1. 一般来说要增删改查链表中的数据，提前先通过利用指针指向对应的节点（一般需要改动一个节点则需要pre、cur、next三个指针记住前、后、自身三个位置）
  2. 正因为上一点中需要用到pre指针，有时候就需要创建一个虚拟的头节点

五、栈，队列，优先队列

栈：栈顶元素反映了在嵌套的层次关系中，最近的需要匹配的元素

栈

20. 有效的括号：给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

示例 1：

1
2
输入：s = "()"
输出：true

示例 2：

1
2
输入：s = "()[]{}"
输出：true

示例 3：

1
2
输入：s = "(]"
输出：false

示例 4：

1
2
输入：s = "([)]"
输出：false

示例 5：

1
2
输入：s = "{[]}"
输出：true

提示：

  • 1<=s.length<=1041 <= s.length <= 10^4
  • s 仅由括号 ‘()[]{}’ 组成

思路：用栈实现，栈顶元素反映了在嵌套的层次关系中，最近的需要匹配的元素

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 时间复杂度: O(n)
// 空间复杂度: O(n)
class Solution {
public:
    bool isValid(string s) {
        stack<char> stack;//创建栈
        for( int i = 0 ; i < s.size() ; i ++ )
            if( s[i] == '(' || s[i] == '{' || s[i] == '[')
                stack.push(s[i]);//左括号全部压栈
            else{
                if( stack.size() == 0 )//确定栈中存在元素
                    return false;

                char c = stack.top();//查看栈顶元素
                stack.pop();//推出栈顶元素
                //根据当前的右括号推断出要匹配左括号
                char match;
                if( s[i] == ')' )
                    match = '(';
                else if( s[i] == ']' )
                    match = '[';
                else{
                    assert( s[i] == '}' );
                    match = '{';
                }

                if(c != match)
                    return false;
            }

        if( stack.size() != 0 )//此时不为0 表示左括号多了
            return false;

        return true;
    }
};

相似题目：150. 逆波兰表达式求值、71. 简化路径

栈和递归（遍历二叉树）

在递归的过程中，系统会将上下文自动压入栈中，这里选取一些递归的例子，在二叉树中较多，举例均为二叉树中的遍历：144. 二叉树的前序遍历、94. 二叉树的中序遍历、145. 二叉树的后序遍历

144. 二叉树的前序遍历：给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

示例1

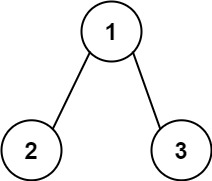
1
2
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

1
2
输入：root = []
输出：[]

示例 3：

1
2
输入：root = [1]
输出：[1]

示例 4：

示例4

1
2
输入：root = [1,2]
输出：[1,2]

示例 5：

示例5

1
2
输入：root = [1,null,2]
输出：[1,2]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

解题：

前序遍历：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/// 时间复杂度: O(n), n为树的节点个数
/// 空间复杂度: O(h), h为树的高度class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        __preorderTraversal(root, res);//递归调用（利用系统自带的栈）
        return res;
    }

private:
    void __preorderTraversal(TreeNode* node, vector<int> &res){
        if(node){
            res.push_back(node->val);
            __preorderTraversal(node->left, res);
            __preorderTraversal(node->right, res);
        }
    }
};

中序遍历：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/// 时间复杂度: O(n), n为树的节点个数
/// 空间复杂度: O(h), h为树的高度
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        __inorderTraversal(root, res);
        return res;
    }

private:
    void __inorderTraversal(TreeNode* node, vector<int> &res){
        if( node ){
            __inorderTraversal(node->left, res);
            res.push_back( node->val );
            __inorderTraversal(node->right, res);
        }
    }
};

后序遍历：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/// 时间复杂度: O(n), n为树的节点个数
/// 空间复杂度: O(h), h为树的高度
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        __postorderTraversal(root, res);
        return res;
    }

private:
    void __postorderTraversal(TreeNode* node, vector<int> &res){
        if( node ){
            __postorderTraversal(node->left, res);
            __postorderTraversal(node->right, res);
            res.push_back(node->val);
        }
    }
};

非递归前序遍历：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/// 时间复杂度: O(n), n为树的节点个数
/// 空间复杂度: O(h), h为树的高度
class Solution {
private:
    struct Command{//自定义数据结构
        string s;   // go, print
        TreeNode* node;
        Command(string s, TreeNode* node): s(s), node(node){}
    };
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root == NULL)
            return res;

        stack<Command> stack;//用自定义数据结构创建栈
        stack.push(Command("go", root));//第一次压栈
        while(!stack.empty()){
            Command command = stack.top();//查看栈顶
            stack.pop();//弹出栈顶

            if(command.s == "print")//先输出
                res.push_back(command.node->val);
            else{//否则去子节点
                assert(command.s == "go");
                if(command.node->right)//取出元素是否有右子节点
                    stack.push(Command("go",command.node->right));//压栈
                if(command.node->left)//取出元素是否有左子节点
                    stack.push(Command("go",command.node->left));//压栈
                stack.push(Command("print", command.node));//将下一个节点压栈
            }
        }
        return res;
    }
};
  • 栈中取出元素和存入元素顺序时反的，所以这里压栈顺序需要反一下
  • 中序遍历后后序遍历仅仅只需要需改压栈顺序即可

相似题目：341. 扁平化嵌套列表迭代器

队列

队列的基本应用就是广度优先遍历（BFS），一般在树和图中用的较多，能够解决以下问题：

  • 树：层序遍历
  • 图：无权图的最短路径

树的层序遍历

102. 二叉树的层序遍历：给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例：
二叉树：[3,9,20,null,null,15,7],

1
2
3
4
5
  3 
 / \
9  20
  /  \
 15   7

返回其层序遍历结果：

1
2
3
4
5
[
  [3],
  [9,20],
  [15,7]
]

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/// 时间复杂度: O(n), n为树的节点个数
/// 空间复杂度: O(n)
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if(root == NULL)
            return res;

        queue<pair<TreeNode*,int>> q;//创建队列（节点信息，所在层数）
        q.push(make_pair(root, 0));//加入队列

        while(!q.empty()){//遍历队列
            TreeNode* node = q.front().first;//取出队列首元素节点信息
            int level = q.front().second;//取出队列首元素层数信息
            q.pop();//将队首元素出队

            if(level == res.size())//如果该层在res中没有 则创建（开辟空间）
                res.push_back(vector<int>());
            assert( level < res.size() );

            res[level].push_back(node->val);//在res中保存该节点值
            if(node->left)
                q.push(make_pair(node->left, level + 1 ));//左节点入队
            if(node->right)
                q.push(make_pair(node->right, level + 1 ));//右节点入队
        }

        return res;
    }
};

相似题目：107. 二叉树的层序遍历 II、103. 二叉树的锯齿形层序遍历、199. 二叉树的右视图

图的最短路径

279. 完全平方数：给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

1
2
3
输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

1
2
3
输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

  • 1<=n<=1041 <= n <= 10^4

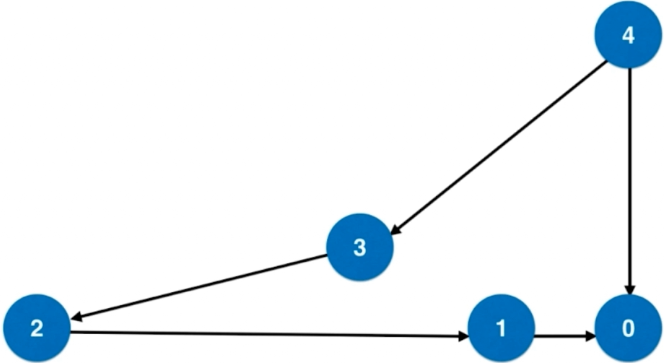
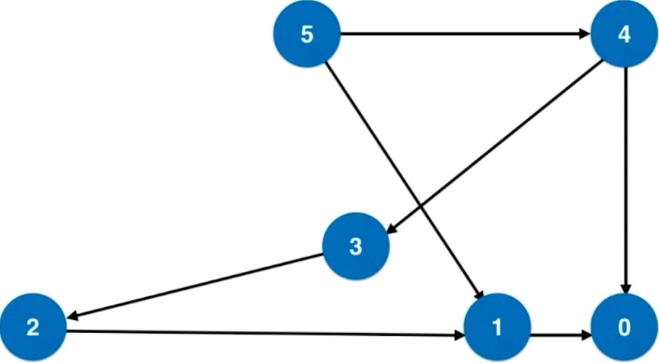
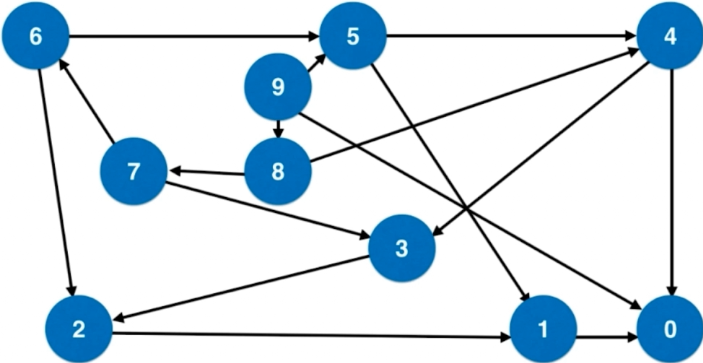
思路：将整个问题转化为一个图论问题：

  • 从n到0，每个数字表示一个节点；
  • 如果两个数字x到y相差一个完全平方数，则连接一条边。

通过上述转发可以将原问题转化为一个从n到0的无权图最短路径问题。其相关情况如下所示：

n=4时的情况

n=5

n=9

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 时间复杂度: O(n)
// 空间复杂度: O(n)
class Solution {
public:
    int numSquares(int n) {
        queue<pair<int, int>> q;//初始化队列 （第几个数字，经历了几段路径到该数字）
        q.push(make_pair(n, 0));//初始化节点n需要0步

        vector<bool> visited(n+1, false);//防止重复推入相同节点到队列中，这里用该变量记录[0,n]有没有被访问过
        visited[n] = true;

        while(!q.empty()){//遍历队列
            int num = q.front().first;
            int step = q.front().second;
            q.pop();//弹出

            if(num == 0)//刚好此时为0的话，表明这就是解
                return step;

            for(int i = 1; num - i * i >= 0; i ++)//如果num还能够承受一个i*i的话
                if(!visited[num - i * i]){//如果未被访问则加入队列
                    q.push(make_pair(num - i * i, step + 1));//入队 （剩余num，对应距离+1）
                    visited[num - i * i] = true;
                }
        }

        throw invalid_argument("No Solution.");
    }
};
  • visited数组很重要，如果没有该变量会导致大量重复节点添加到队列中
  • num - i * i可以提取出来计算一次，而非多次计算
  • if(num == 0)其实可以在推入队列时就能检查出来，此时step = step+1
  • 四平方法（数学方法）能够很轻松的解决该问题

相似题目：127. 单词接龙、126. 单词接龙 II

优先队列

优先队列的底层实现一般是通过堆来实现

C++中通过priority_queue来表示优先队列（默认为最大堆，按照从大到小排序输出），一般用来维护前k大/小的元素，每次 push(x)/pop() 操作的时间复杂度是O(logn)O(logn)，其基本使用样例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
bool myCmp(int a , int b){//自定义比较函数
    if(a%10 != b%10)
        return a%10 > b%10;
    return a > b;
}

int main() {
    srand(time(NULL));
    // 默认的priority queue, 底层是最大堆
    priority_queue<int> pq;//创建
    for(int i = 0 ; i < 10 ; i ++){
        int num = rand() % 100;
        pq.push(num);//入队
        cout << "insert " << num << " in priority queue." << endl;
    }
    while(!pq.empty()){
        cout << pq.top() << " ";//查看
        pq.pop();//出队
    }
    cout << endl << endl;

    // 使用greater的priority queue, 底层是最小堆
    priority_queue<int, vector<int>, greater<int>> pq2;//创建最小堆 <元素类型，底层数据结构实现，比较函数>
    ...

    // 使用自定义Comparator的priority queue
    priority_queue<int, vector<int>, function<bool(int,int)>> pq3(myCmp);
    ...
}

347. 前 K 个高频元素：给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

1
2
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

1
2
输入: nums = [1], k = 1
输出: [1]

提示：

  • 你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
  • 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
  • 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。
  • 你可以按任意顺序返回答案。

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 时间复杂度: O(nlogk)
// 空间复杂度: O(n + k)
class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        assert(k > 0);
        // 统计每个元素出现的频率
        unordered_map<int,int> freq;//<元素， 对应的频率>
        for(int i = 0 ; i < nums.size() ; i ++ )
            freq[nums[i]] ++;

        assert(k <= freq.size());

        // 扫描freq,维护当前出现频率最高的k个元素
        // 在优先队列中,按照频率排序,所以数据对是 (频率,元素) 的形式（pair先比较第一个元素）
        priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;//创建最小堆的优先队列
        for(unordered_map<int,int>::iterator iter = freq.begin(); iter != freq.end(); iter ++ ){//遍历map，即出现频率
            if(pq.size() == k){//已经出现k个
                if(iter->second > pq.top().first){//比较频率，注意这两个pair中元素是反着放的
                    pq.pop();//弹出队首元素，即频率最低那个
                    pq.push( make_pair(iter->second, iter->first));//将新的元素入队
                }
            }else//还没满k个，直接入队即可
                pq.push(make_pair(iter->second , iter->first));
        }

        vector<int> res;
        while(!pq.empty()){//遍历优先队列
            res.push_back(pq.top().second);//加入数组
            pq.pop();//弹出队列首部元素
        }

        return res;
    }
};
  • 当k接进与n时，上述算法会退化为O(nlogn)
  • 可以通过在优先队列中只维护n-k个元素来完成O(nlog(n-k))的时间复杂度

相似题目：23. 合并K个升序链表

总结与感悟

  1. 队列deque可以理解为能够双端插入的vector，push_front/push_back/pop_front/pop_back均为O(1)O(1)，insert/erase均为O(n)O(n)
  2. 优先队列每次 push()/pop() 操作的时间复杂度是O(logn)O(logn)
  3. 优先队列能够解决一些排序题目，只需要将要排序的数据放到优先队列中，同时可以在该数据下挂一个其他数据（利用pair或自定义数据结构），如上述 leetcode 347和23题
  4. 有些题规定不能用递归实现时可以考虑用栈来模拟

六、二叉树和递归

之前讲过递归可以参考：[栈和递归（遍历二叉树）](# 栈和递归（遍历二叉树）)

二叉树具有天然的递归结构：

  • 终止条件
  • 递归过程

天然的递归结构

104. 二叉树的最大深度：给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

给定二叉树 [3,9,20,null,null,15,7]，

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回它的最大深度 3 。

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
// 时间复杂度: O(n), n是树中的节点个数
// 空间复杂度: O(h), h是树的高度
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL)//递归终止条件
            return 0;

        return 1 + max(maxDepth(root->left), maxDepth(root->right));//递归过程
    }
};

相似题目：111. 二叉树的最小深度

226. 翻转二叉树：翻转一棵二叉树。

示例：

输入：

1
2
3
4
5
     4
   /   \
  2     7
 / \   / \
1   3 6   9

输出：

1
2
3
4
5
     4
   /   \
  7     2
 / \   / \
9   6 3   1

备注:

这个问题是受到 Max Howell 的 原问题 启发的 ：

谷歌：我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/// 时间复杂度: O(n), n为树中节点个数
/// 空间复杂度: O(h), h为树的高度
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root == NULL)//递归终止条件
            return NULL;

        invertTree(root->left);//递归过程
        invertTree(root->right);
        swap(root->left, root->right);

        return root;
    }
};

相似题目：100. 相同的树、101. 对称二叉树、222. 完全二叉树的节点个数、110. 平衡二叉树

完全二叉树：除了最后一层，所有层的节点数达到最大，与此同时，最后一层的所有节点都在最左侧。

满二叉树：所有层的节点数达到最大。

平衡二叉树：每一个节点的左右子树的高度差不超过1

二分搜索树：每个节点的键值大于左孩子；每个节点的键值小于右孩子；且以左右孩子为根的子树仍为二分搜索树

注意终止条件

有时候递归的终止条件不能简单地想当然，如下题就需要认真分析：

112. 路径总和：给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ，判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。

叶子节点 是指没有子节点的节点。

示例 1：

示例1

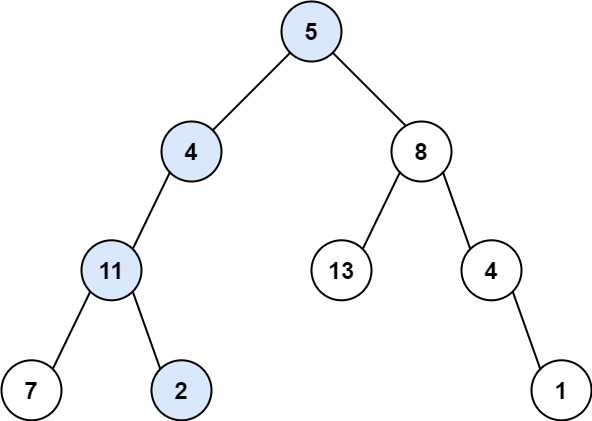
1
2
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true

示例 2：

示例2

1
2
输入：root = [1,2,3], targetSum = 5
输出：false

示例 3：

1
2
输入：root = [1,2], targetSum = 0
输出：false

提示：

  • 树中节点的数目在范围 [0, 5000] 内
  • -1000 <= Node.val <= 1000
  • -1000 <= targetSum <= 1000

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
（此时才为叶子节点）/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/// 时间复杂度: O(n), n为树的节点个数
/// 空间复杂度: O(h), h为树的高度
class Solution {
public:
    bool hasPathSum(TreeNode* root, int sum) {
        if(root == NULL)//递归终止条件（判断传入的root是否为NULL）
            return false;

        if(root->left == NULL && root->right == NULL)//递归终止条件（此时才为叶子节点）
            return sum == root->val;

        return hasPathSum(root->left, sum - root->val)
                || hasPathSum(root->right, sum - root->val);//递归过程
    }
};

注意：上述这道题很容易按照以下写法：

1
2
3
4
5
6
7
8
9
10
bool hasPathSum(TreeNode* root, int sum) {
    if(root == NULL)//终止条件错误，不能判断上一层节点是否为叶子节点
        return sum == 0;
    
    if(hasPathSum( root->left, sum - root->val))
        return true;
    
    if(hasPathSum( root->right, sum - root->val))
        return true;
}

此时，如果遇到以下二叉树：

1
2
3
4
5
 5
  \
   8
 /  \
13   4

当此时的sum为5时，会立马退出递归。而节点5不是叶子节点（应该注意叶子节点为左右节点均为NULL）。此问题处在终止条件上，忽视了上一层是否为叶子节点

相似题目：111. 二叉树的最小深度、404. 左叶子之和

稍复杂的递归逻辑

递归的返回值也可以很复杂，如返回一个数组：

257. 二叉树的所有路径：给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

1
2
3
4
5
6
7
8
输入:
   1
 /   \
2     3
 \
  5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/// 时间复杂度: O(n), n为树中的节点个数
/// 空间复杂度: O(h), h为树的高度
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> res;
        if(root == NULL)//终止条件——防止root为空
            return res;

        if(root->left == NULL && root->right == NULL){//终止条件——叶子节点
            res.push_back(to_string(root->val));
            return res;
        }

        vector<string> leftPaths = binaryTreePaths(root->left);//遍历左子树，将结果放到字符串数组中
        for(int i = 0 ; i < leftPaths.size() ; i ++)
            res.push_back(to_string(root->val) + "->" + leftPaths[i]);

        vector<string> rightPaths = binaryTreePaths(root->right);//遍历右子树，将结果放到字符串数组中
        for(int i = 0 ; i < rightPaths.size() ; i ++)
            res.push_back(to_string(root->val) + "->" + rightPaths[i]);

        return res;
    }
};

相似题目：113. 路径总和 II、129. 求根到叶子节点数字之和

更复杂的递归问题

437. 路径总和 III：给定一个二叉树，它的每个结点都存放着一个整数值。

找出路径和等于给定数值的路径总数。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

二叉树不超过1000个节点，且节点数值范围是 [-1000000,1000000] 的整数。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1
返回 3。和等于 8 的路径有:
1.  5 -> 3
2.  5 -> 2 -> 1
3.  -3 -> 11

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/// 时间复杂度: O(n), n为树的节点个数
/// 空间复杂度: O(h), h为树的高度
class Solution {
public:
    // 在以root为根节点的二叉树中,寻找和为sum的路径,返回这样的路径个数
    int pathSum(TreeNode* root, int sum) {

        if(root == NULL)
            return 0;

        return findPath(root, sum)//包含root节点且和为sum
                + pathSum(root->left , sum)//不包含root节点且和为sum
                + pathSum(root->right , sum);//不包含root节点且和为sum
    }

private:
    // 在以node为根节点的二叉树中,寻找包含node的路径,和为sum
    // 返回这样的路径个数
    int findPath(TreeNode* node, int num){
        if(node == NULL)//终止条件——没有要求必须为叶子节点
            return 0;

        int res = 0;
        if(node->val == num)
            res += 1;

        //由于节点上存在负数，除了上述node->val == num外，还有可能在之后仍存在== num的情况
        res += findPath(node->left , num - node->val);
        res += findPath(node->right , num - node->val);

        return res;
    }
};

二分搜索树中问题

完全二叉树：除了最后一层，所有层的节点数达到最大，与此同时，最后一层的所有节点都在最左侧。

满二叉树：所有层的节点数达到最大。

平衡二叉树：每一个节点的左右子树的高度差不超过1

二分搜索树：每个节点的键值大于左孩子；每个节点的键值小于右孩子；且以左右孩子为根的子树仍为二分搜索树

基本操作（时间复杂度均为lognlogn）：

  • 插入 insert
  • 查找 find
  • 删除 delete
  • 顺序性：
    • 最大值，最小值 minimum, maximum
    • 前驱，后继 successor, predecessor
    • 上界，下界 floor,ceil
    • 某个元素的排名 rank
    • 寻找第k大（小）元素 select

235. 二叉搜索树的最近公共祖先：给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

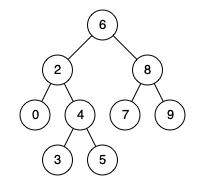
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

二叉搜索树

示例 1:

1
2
3
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

1
2
3
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

  • 所有节点的值都是唯一的。
  • p、q 为不同节点且均存在于给定的二叉搜索树中。

思路：由于是二叉搜索树，所以可以通过判断根节点（root）和待判断节点（p、q）的大小来确定目标节点在根节点的那个子树中：

  1. root>q，root>p：在root的左子树中寻找
  2. root<q，root<p：在root的右子树中寻找
  3. root>q，root<p或root<q，root>p：root节点就是目标节点，这其中有两种特例：
    1. p==root
    2. q==root

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
/// 时间复杂度: O(lgn), 其中n为树的节点个数
/// 空间复杂度: O(h), 其中h为树的高度
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        assert(p != NULL && q != NULL);

        if(root == NULL)//防止root为空
            return NULL;

        if(p->val < root->val && q->val < root->val)//必定在左子树中
            return lowestCommonAncestor(root->left, p, q);
        if(p->val > root->val && q->val > root->val)//必定在右子树中
            return lowestCommonAncestor(root->right, p, q);

        assert(p->val == root->val || q->val == root->val || (root->val - p->val) * (root->val - q->val) < 0);//检查整棵树中存在p、q

        return root;
    }
};

相似题目：98. 验证二叉搜索树、450. 删除二叉搜索树中的节点（删除节点是二分搜索树中最难的操作）、108. 将有序数组转换为二叉搜索树（中序遍历二分搜索树时，就是将其从小到大进行排列）、230. 二叉搜索树中第K小的元素、236. 二叉树的最近公共祖先（Lowest Common Ancestor of a Binary Tree，即经典的LCA问题）

总结和感悟

  1. 在二叉树递归时，如果明确要求要考虑二叉树的叶子节点，则必须要有如下终止条件：

    1
    if(root->left == NULL && root->right == NULL)

    否则：

    1
    if(node == NULL)

    即可

  2. 中序遍历二分搜索树时，就是将其从小到大进行排列

  3. 前序遍历先访问根节点。后序遍历最后访问根节点。中序遍历先访问左子树，再访问根节点，最后访问右子树

  4. 在根据二叉树中序遍历+前序遍历/后序遍历重构二叉树的过程中，需要根据前序遍历/后序遍历来找到根节点，再在中序遍历中插叙此节点（可以通过map加速），此时中序遍历的根节点的前半部分为左子树，后半部分为右子树，此时再递归即可解决

  5. 二叉树特例：

    1. 二叉搜索树
    2. 堆
      1. 最大堆：根节点的值最大
      2. 最小堆：根节点的值最小
    3. 红黑树

七、递归和回溯法

树形问题及回溯

这类问题本身不是在一颗二叉树这样的结构中，但是具体分析时解决该问题的思路本质就是一颗树的形状

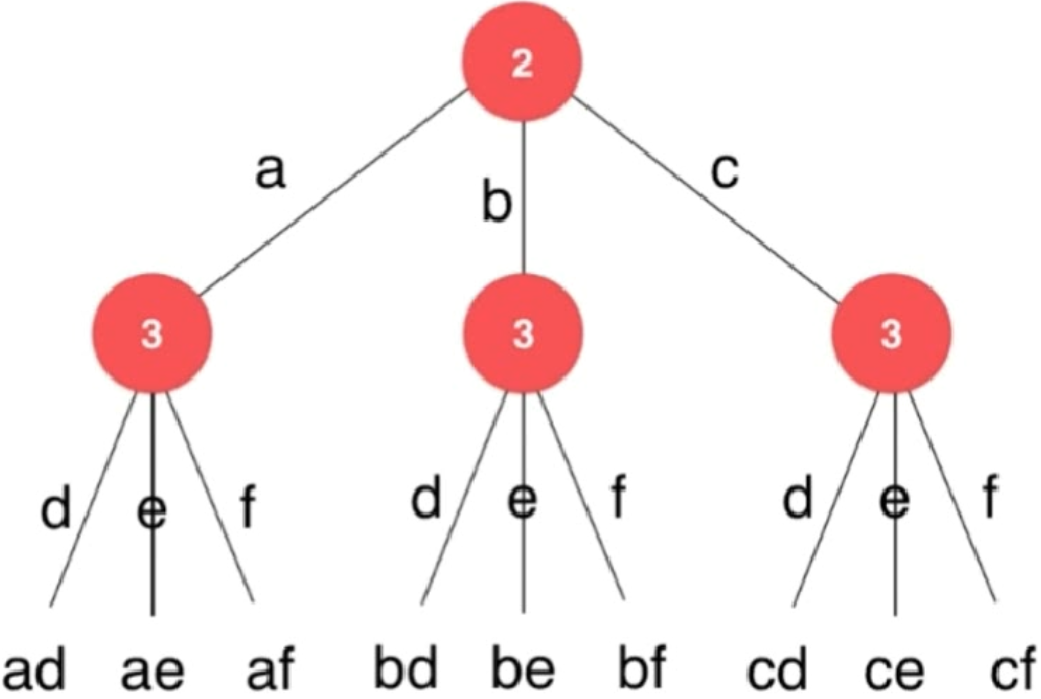
17. 电话号码的字母组合：给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

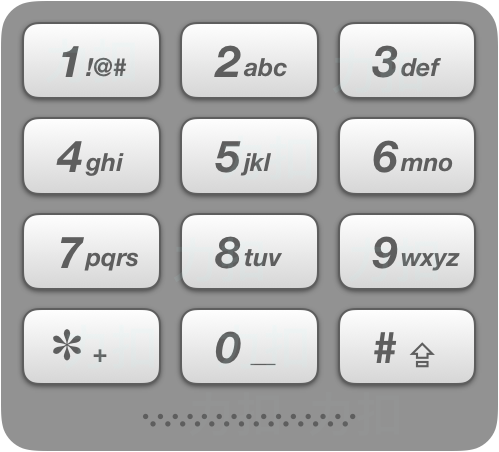
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

电话按键

示例 1：

1
2
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

1
2
输入：digits = ""
输出：[]

示例 3：

1
2
输入：digits = "2"
输出：["a","b","c"]

提示：

  • 0 <= digits.length <= 4
  • digits[i] 是范围 [‘2’, ‘9’] 的一个数字。

思路：

假设digits = “23”，则此时可以将解视为如下所示的一个树：

递归搜索树

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
/// 时间复杂度: O(2^len(s))
/// 空间复杂度: O(len(s))
class Solution {
private:
    const string letterMap[10] = {//保存数字对应的字母表
            " ",    //0
            "",     //1
            "abc",  //2
            "def",  //3
            "ghi",  //4
            "jkl",  //5
            "mno",  //6
            "pqrs", //7
            "tuv",  //8
            "wxyz"  //9
    };

    vector<string> res;

    // digits：要处理的数字字符串	
    // index：每次处理时，处理的数字字符串中的索引
    // s：每次处理时之前处理过的数保存在s中
    // s中保存了此时从digits[0...index-1]翻译得到的一个字母字符串
    // 在该函数中只需要寻找和digits[index]匹配的字母, 获得digits[0...index]翻译得到的解
    void findCombination(const string &digits, int index, const string &s){

        cout << index << " : " << s << endl;
        if(index == digits.size()){//最终一次递归结束，此时应该得到一个解
            res.push_back(s);
            cout << "get " << s << " , return" << endl;
            return;
        }

        char c = digits[index];//获得index处的数字字符
        assert(c >= '0' && c <= '9' && c != '1');
        string letters = letterMap[c - '0'];//取出数字对应的所有字母
        for(int i = 0 ; i < letters.size() ; i ++){//遍历字母
            cout << "digits[" << index << "] = " << c << " , use " << letters[i] << endl;
            findCombination(digits, index+1, s + letters[i]);//递归后一个字母
        }

        cout << "digits[" << index << "] = " << c << " complete, return" << endl;

        return;
    }

public:
    vector<string> letterCombinations(string digits) {
        res.clear();//清楚最终数组中的值
        if(digits == "")
            return res;

        findCombination(digits, 0, "");//开始递归求解
        return res;
    }
};
  • 时间复杂度3n=O(2n)3^n=O(2^n)

上述输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
0 : 
digits[0] = 2 , use a
1 : a
digits[1] = 3 , use d
2 : ad
digits[2] = 4 , use g
3 : adg
get adg , return
digits[2] = 4 , use h
3 : adh
get adh , return
digits[2] = 4 , use i
3 : adi
get adi , return
digits[2] = 4 complete, return
digits[1] = 3 , use e
2 : ae
digits[2] = 4 , use g
3 : aeg
get aeg , return
digits[2] = 4 , use h
3 : aeh
get aeh , return
digits[2] = 4 , use i
3 : aei
get aei , return
digits[2] = 4 complete, return
digits[1] = 3 , use f
2 : af
digits[2] = 4 , use g
3 : afg
get afg , return
digits[2] = 4 , use h
3 : afh
get afh , return
digits[2] = 4 , use i
3 : afi
get afi , return
digits[2] = 4 complete, return
digits[1] = 3 complete, return
digits[0] = 2 , use b
1 : b
digits[1] = 3 , use d
2 : bd
digits[2] = 4 , use g
3 : bdg
get bdg , return
digits[2] = 4 , use h
3 : bdh
get bdh , return
digits[2] = 4 , use i
3 : bdi
get bdi , return
digits[2] = 4 complete, return
digits[1] = 3 , use e
2 : be
digits[2] = 4 , use g
3 : beg
get beg , return
digits[2] = 4 , use h
3 : beh
get beh , return
digits[2] = 4 , use i
3 : bei
get bei , return
digits[2] = 4 complete, return
digits[1] = 3 , use f
2 : bf
digits[2] = 4 , use g
3 : bfg
get bfg , return
digits[2] = 4 , use h
3 : bfh
get bfh , return
digits[2] = 4 , use i
3 : bfi
get bfi , return
digits[2] = 4 complete, return
digits[1] = 3 complete, return
digits[0] = 2 , use c
1 : c
digits[1] = 3 , use d
2 : cd
digits[2] = 4 , use g
3 : cdg
get cdg , return
digits[2] = 4 , use h
3 : cdh
get cdh , return
digits[2] = 4 , use i
3 : cdi
get cdi , return
digits[2] = 4 complete, return
digits[1] = 3 , use e
2 : ce
digits[2] = 4 , use g
3 : ceg
get ceg , return
digits[2] = 4 , use h
3 : ceh
get ceh , return
digits[2] = 4 , use i
3 : cei
get cei , return
digits[2] = 4 complete, return
digits[1] = 3 , use f
2 : cf
digits[2] = 4 , use g
3 : cfg
get cfg , return
digits[2] = 4 , use h
3 : cfh
get cfh , return
digits[2] = 4 , use i
3 : cfi
get cfi , return
digits[2] = 4 complete, return
digits[1] = 3 complete, return
digits[0] = 2 complete, return
adg
adh
adi
aeg
aeh
aei
afg
afh
afi
bdg
bdh
bdi
beg
beh
bei
bfg
bfh
bfi
cdg
cdh
cdi
ceg
ceh
cei
cfg
cfh
cfi
  • 可以看出，递归调用的一个重要特性——返回回溯
  • 回溯法是暴力解法的一个主要实现手段

相似题目：93. 复原 IP 地址、131. 分割回文串

回溯问题

排列问题

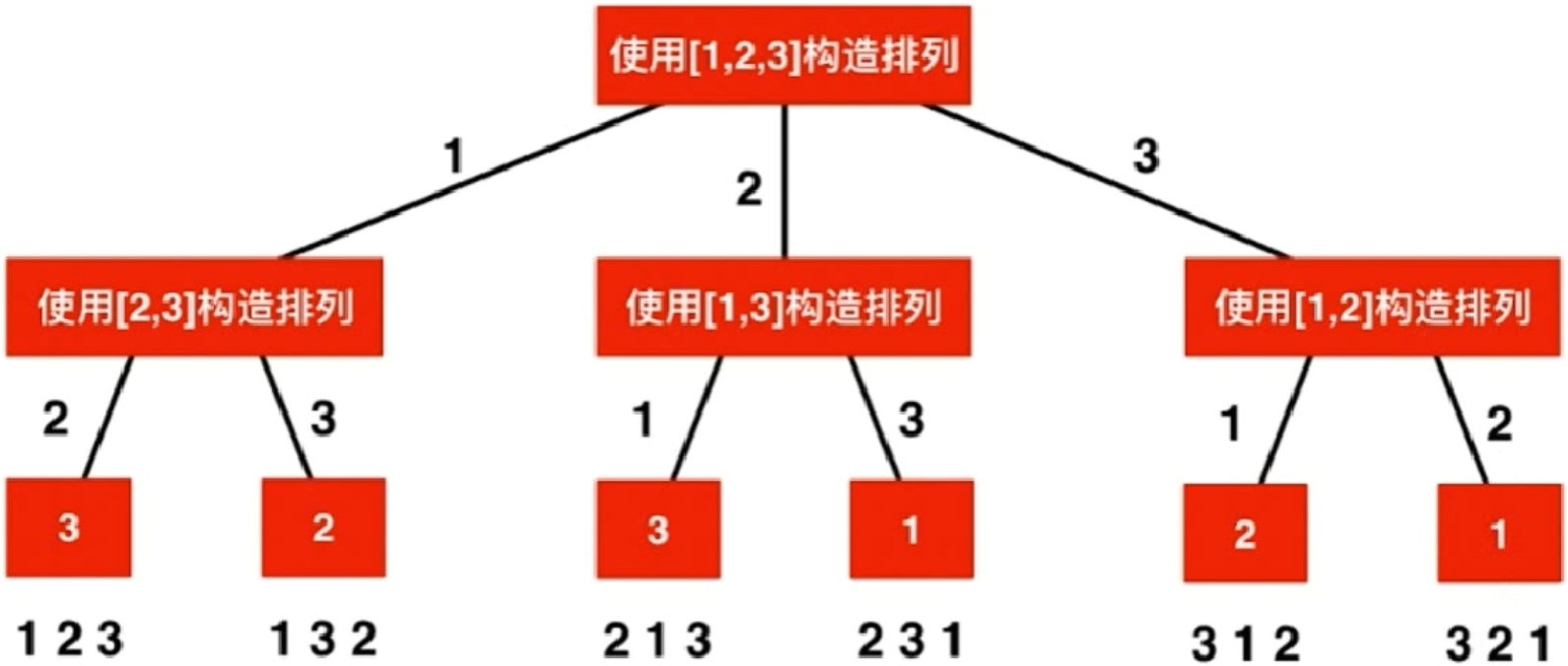
46. 全排列：给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

1
2
3
4
5
6
7
8
9
10
输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

思路：

根据回溯的想法，该题中需要在每一步中选出一个元素，则有：

回溯树（递归搜索树）

求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/// 时间复杂度: O(n^n)
/// 空间复杂度: O(n)
class Solution {
private:
    vector<vector<int>> res;//已经找到的全部排列
    vector<bool> used;//nums中第i个元素是否已经使用过

    // p中保存了一个有index-1个元素的排列。
    // 向这个排列的末尾添加第index个元素, 获得一个有index个元素的排列
    void generatePermutation(const vector<int>& nums, int index, vector<int>& p){
        if(index == nums.size()){//排列已经找到
            res.push_back(p);
            return;
        }

        for(int i = 0 ; i < nums.size() ; i ++)
            if(!used[i]){//如果第i个元素未使用
                used[i] = true;
                p.push_back(nums[i]);
                generatePermutation(nums, index + 1, p );//递归调用，获得一个排列
                p.pop_back();//回溯时，p中弹出当前元素
                used[i] = false;//回溯时，该元素未访问
            }

        return;
    }

public:
    vector<vector<int>> permute(vector<int>& nums) {
        res.clear();
        if(nums.size() == 0)//排除非法参数
            return res;

        used = vector<bool>(nums.size(), false);
        vector<int> p;
        generatePermutation(nums, 0, p);//递归获取全部排列

        return res;
    }
};
  • 注意状态的回溯
  • 如果需要考虑重复，需要用到set排除
  • 可以用swap交换替代used表示，节省空间

相似题目：47. 全排列 II、剑指 Offer 38. 字符串的排列

组合问题

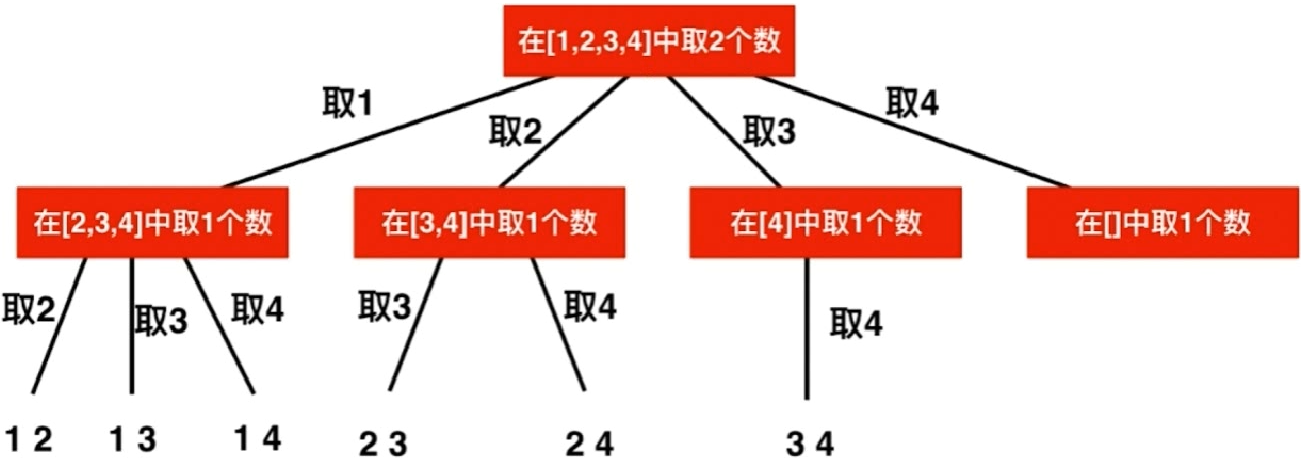
77. 组合：给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

1
2
3
4
5
6
7
8
9
10
输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

思路：

通过先取不同的数据，随后再取剩下的数，可以得到如下的树状图：

回溯树（递归搜索树）

  • 组合问题中，不会考虑取出数字的顺序

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/// 时间复杂度: O(n^k)
/// 空间复杂度: O(k)
class Solution {
private:
    vector<vector<int>> res;
    // 求解C(n,k), 当前已经找到的组合存储在c中, 需要从start开始搜索新的元素
    void generateCombinations(int n, int k, int start, vector<int> &c){
        if(c.size() == k){//已经找到对应的组合
            res.push_back(c);
            return;
        }

        for(int i = start ; i <= n ; i ++){
            c.push_back( i );//先放入i
            generateCombinations(n, k, i + 1, c);//递归调用，求剩下元素中的组合
            c.pop_back();//回溯时，返回之前状态
        }

        return;
    }
public:
    vector<vector<int>> combine(int n, int k) {
        res.clear();
        if( n <= 0 || k <= 0 || k > n )
            return res;

        vector<int> c;
        generateCombinations(n, k, 0, c);
        return res;
    }
};
优化——剪枝

在上述问题中，通过回溯树可以看出，在最后取出4时是没必要的，可以通过剪枝操作来优化该算法（将一些不可能的情况去掉不去搜索），尤其是当k较大时更加明显

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/// 时间复杂度: O(n^k)
/// 空间复杂度: O(k)
class Solution {
private:
    vector<vector<int>> res;
    // 求解C(n,k), 当前已经找到的组合存储在c中, 需要从start开始搜索新的元素
    void generateCombinations(int n, int k, int start, vector<int> &c){
        if(c.size() == k){
            res.push_back(c);
            return;
        }

        // 还有k - c.size()个空位, 所以, [i...n] 中至少要有 k - c.size() 个元素
        // i最多为 n - (k - c.size()) + 1
        for(int i = start; i <= n - (k - c.size()) + 1 ; i ++){//剪枝操作
            c.push_back(i);
            generateCombinations(n, k, i + 1 ,c);
            c.pop_back();
        }

        return;
    }
public:
    vector<vector<int>> combine(int n, int k) {
        res.clear();
        if(n <= 0 || k <= 0 || k > n)
            return res;

        vector<int> c;
        generateCombinations(n, k, 1, c);
        return res;
    }
};

  • 上述代码和之前比，仅仅只多出了剪枝操作
  • 当k较大时运行时间会大大缩减

相似问题：39. 组合总和、40. 组合总和 II、216. 组合总和 III、78. 子集、90. 子集 II、401. 二进制手表

二维平面问题

回溯法

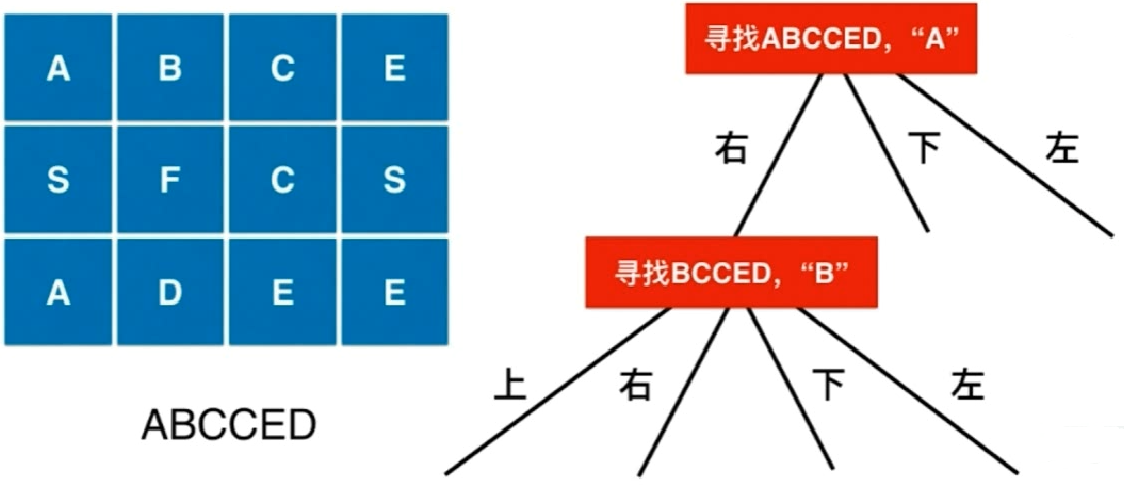
79. 单词搜索：给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

1
2
3
4
5
6
7
8
9
board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]
给定 word = "ABCCED", 返回 true
给定 word = "SEE", 返回 true
给定 word = "ABCB", 返回 false

提示：

  • board 和 word 中只包含大写和小写英文字母。
  • 1 <= board.length <= 200
  • 1 <= board[i].length <= 200
  • 1 <= word.length <= 10^3

思路：

在给定的图中一直不断查找是否存在对应word中的字母，不存在就回退，否则就想四周（上下左右）查找

回溯树（递归搜索树）

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/// 时间复杂度: O(m*n*m*n)
/// 空间复杂度: O(m*n)
class Solution {
private:
    int d[4][2] = {{-1, 0}, {0,1}, {1, 0}, {0, -1}};//四个方向
    int m, n;//整个二维图的行和列
    vector<vector<bool>> visited;//已经访问过

    //判断坐标[x,y]是否为合法坐标
    bool inArea(int x, int y){
        return x >= 0 && x < m && y >= 0 && y < n;
    }

    // 从board[startx][starty]开始, 寻找word[index...word.size())
    bool searchWord(const vector<vector<char>> &board, const string& word, int index, int startx, int starty ){
        //assert(inArea(startx,starty));
        if(index == word.size() - 1)//如果是最后一个字符 就直接比较
            return board[startx][starty] == word[index];

        //不是最后一个字符 直接搜索
        if(board[startx][starty] == word[index]){
            visited[startx][starty] = true;
            // 从startx, starty出发,向四个方向寻
            for(int i = 0 ; i < 4 ; i ++){
                int newx = startx + d[i][0];
                int newy = starty + d[i][1];
                if(inArea(newx, newy) && !visited[newx][newy] &&//[newx,newy]未越界且未被访问
                   searchWord(board, word, index + 1, newx, newy))//递归搜索
                    return true;
            }
            visited[startx][starty] = false;//回溯 返回之前的状态
        }
        return false;
    }

public:
    bool exist(vector<vector<char>>& board, string word) {
        m = board.size();//行
        assert(m > 0);
        n = board[0].size();//列
        assert(n > 0);

        visited.clear();
        for(int i = 0 ; i < m ; i ++)
            visited.push_back(vector<bool>(n, false));

        for(int i = 0 ; i < board.size() ; i ++)
            for(int j = 0 ; j < board[i].size() ; j ++)
                if(searchWord(board, word, 0, i, j))//遍历整个二维图 查找对应字符串
                    return true;

        return false;
    }
};

floodfill算法

类似与洪水扩散，由一个点一直向外扩撒，其本质就是深度优先遍历

200. 岛屿数量：给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

1
2
3
4
5
6
7
输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

1
2
3
4
5
6
7
输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 300
  • grid[i][j] 的值为 ‘0’ 或 ‘1’

思路：

从一个块开始查找，反复查找相邻的且未被访问过的相同块，直到不同类型的块

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/// 时间复杂度: O(n*m)
/// 空间复杂度: O(n*m)
class Solution {
private:
    int d[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};//位移数组 四个方向
    int m, n;//行列
    vector<vector<bool>> visited;//是否访问的标志

    //判断坐标是否合法
    bool inArea(int x, int y){
        return x >= 0 && x < m && y >= 0 && y < n;
    }

    // 从grid[x][y]的位置开始,进行floodfill
    // 保证(x,y)合法,且grid[x][y]是没有被访问过的陆地
    void dfs(vector<vector<char>>& grid, int x, int y){
        //assert(inArea(x,y));
        visited[x][y] = true;
        for(int i = 0; i < 4; i ++){//四个方向遍历
            int newx = x + d[i][0];
            int newy = y + d[i][1];
            if(inArea(newx, newy) && !visited[newx][newy] && grid[newx][newy] == '1')//新位置未越界、未被访问、且为陆地——终止条件
                dfs(grid, newx, newy);//搜索新的位置
        }

        return;
    }

public:
    int numIslands(vector<vector<char>>& grid) {
        m = grid.size();
        if(m == 0)
            return 0;
        n = grid[0].size();
        if(n == 0)
            return 0;

        for(int i = 0 ; i < m ; i ++)
            visited.push_back(vector<bool>(n, false));

        int res = 0;
        for(int i = 0 ; i < m ; i ++)
            for(int j = 0 ; j < n ; j ++)//遍历地图
                if(grid[i][j] == '1' && !visited[i][j]){//未访问且为陆地
                    dfs(grid, i, j);//floodfill算法标记一块陆地
                    res ++;
                }
        return res;
    }
};

相似问题：130. 被围绕的区域、417. 太平洋大西洋水流问题

N皇后问题

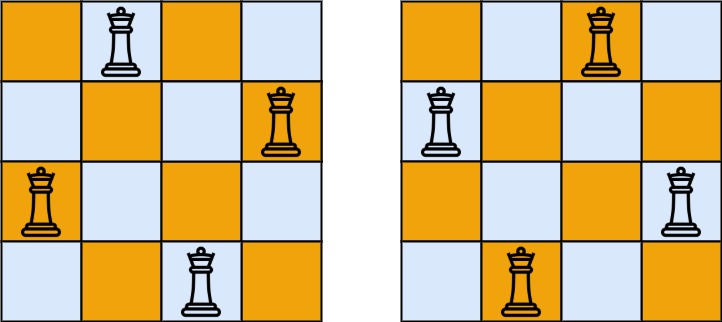
51. N 皇后：n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1：

示例1

1
2
3
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

1
2
输入：n = 1
输出：[["Q"]]

提示：

  • 1 <= n <= 9
  • 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

思路：

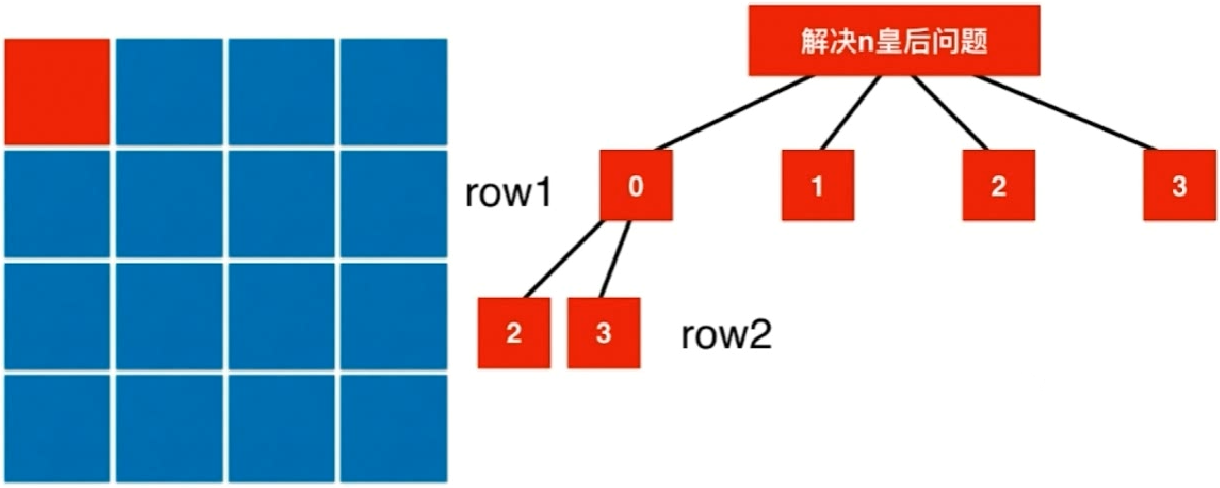
仍然是回溯，一个位置一个位置尝试（每一行先摆放一个，在下一行摆放时需要考虑前面摆放的皇后位置），有以下递归树：

回溯树（递归搜索树）

但是不合法情况的判断较为复杂（根据此来剪枝），这里通过如下方式判断：

  1. 竖向：通过一个数组col[i]来表示第i列被占用

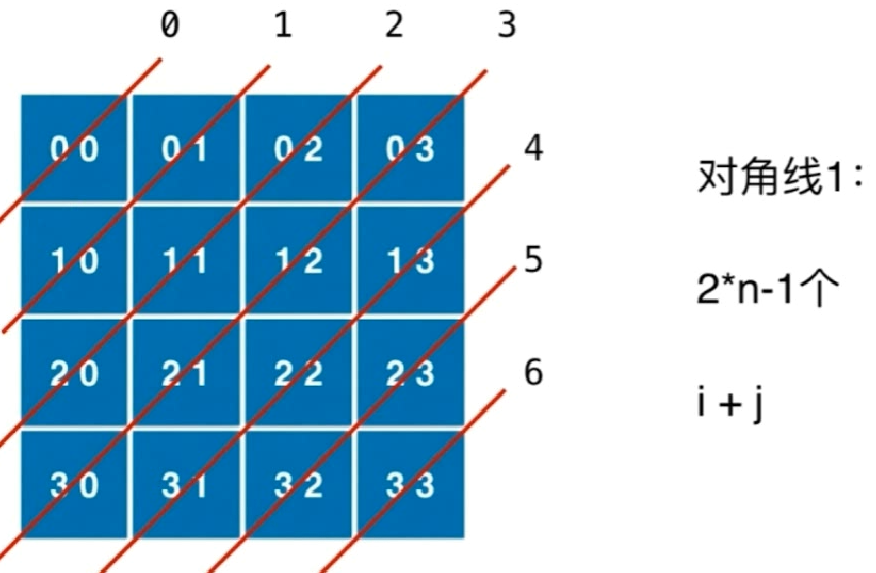
  2. 对角线1：通过一个数组dia1[i]来表示第i对角线1被占用

    对角线1

    • 这种对角线一共有2*n-1条，其中n为行数
    • 每行可以通过dia1[i+j]来访问，其中i、j为对应位置的坐标序号

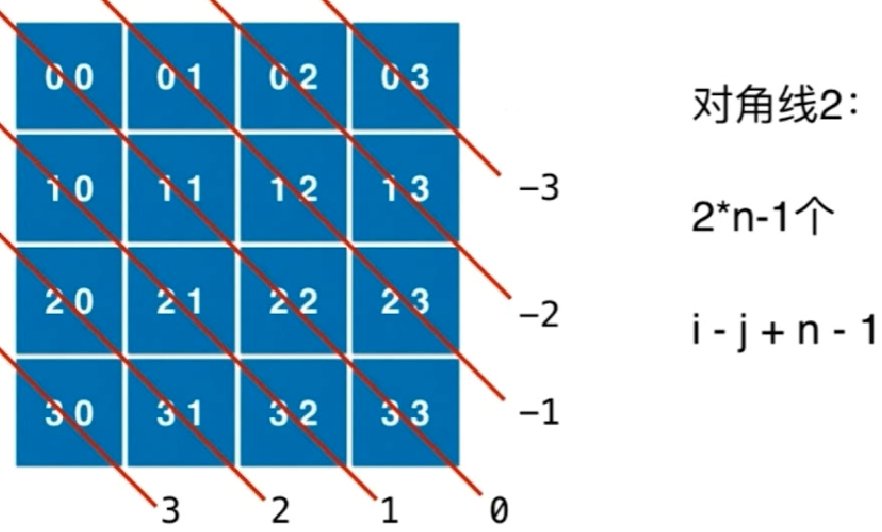
  3. 对角线2：通过一个数组dia2[i]来表示第i对角线2被占用

    对角线2

    • 这种对角线一共有2*n-1条，其中n为行数
    • 每行可以通过dia2[i-j+n-1]来访问（i-j存在偏置，需要通过n-1来矫正到正数），其中i、j为对应位置的坐标序号

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
/// 时间复杂度: O(n^n)
/// 空间复杂度: O(n)
class Solution {
private:
    vector<bool> col, dia1, dia2;//列（索引为对应的行号）、对角线1、对角线2
    vector<vector<string>> res;//最终返回结果

    // 尝试在一个n皇后问题中, 摆放第index行的皇后位置，结果存放在row中
    void putQueen(int n, int index, vector<int> &row){
        //递归终止条件
        if(index == n){ 
            res.push_back(generateBoard(n, row));//将一个可行解进行保存
            return;
        }

        for(int i = 0 ; i < n ; i ++)//遍历一行中的每一列
            // 尝试将第index行的皇后摆放在第i列
            if(!col[i] && !dia1[index + i] && !dia2[index - i + n - 1]){//列、对角线1、对角线2上均无其他皇后
                //假设该列摆放皇后
                row.push_back(i);//保存该列
                col[i] = true;//标识该列已被占用
                dia1[index + i] = true;//标识该对角线1已被占用
                dia2[index - i + n - 1] = true;//标识该对角线2已被占用
                putQueen(n, index + 1, row);//递归调用 尝试求解下一行可能的解
                //回溯 返回之前状态 尝试下一列摆放皇后
                col[i] = false;
                dia1[index + i] = false;
                dia2[index - i + n - 1] = false;
                row.pop_back();
            }

        return;
    }

    //转换函数
    vector<string> generateBoard(int n, vector<int> &row){
        assert(row.size() == n);
        vector<string> board(n, string(n, '.'));
        for(int i = 0 ; i < n ; i ++)
            board[i][row[i]] = 'Q';
        return board;
    }

public:
    vector<vector<string>> solveNQueens(int n) {

        res.clear();

        col.clear();
        for(int i = 0 ; i < n ; i ++)
            col.push_back(false);

        dia1.clear();
        dia2.clear();
        for(int i = 0 ; i < 2 * n - 1 ; i ++){
            dia1.push_back(false);
            dia2.push_back(false);
        }

        vector<int> row;
        putQueen(n, 0, row);//递归求解

        return res;
    }
};

相似问题：52. N皇后 II、37. 解数独

总结和感悟

  1. 在二维数组中搜索路径时，可以尝试用回溯法，并且通常很适合用递归实现
    1. 搜索问题一般可以用到深度优先遍历和广度优先遍历（回溯法在某种角度下就是深度优先遍历）
      1. 深度优先遍历一般需要递归，所以需要用到状态+子问题
      2. 广度优先遍历需要通过队列
  2. 回溯法非常适合由多个步骤组成的问题，并且每个步骤都有多个选项

八、动态规划基础

动态规划：将原问题拆解成若干子问题，同时保存子问题的答案，使得每个子问题只求解一次，最终获得原问题的笞案。

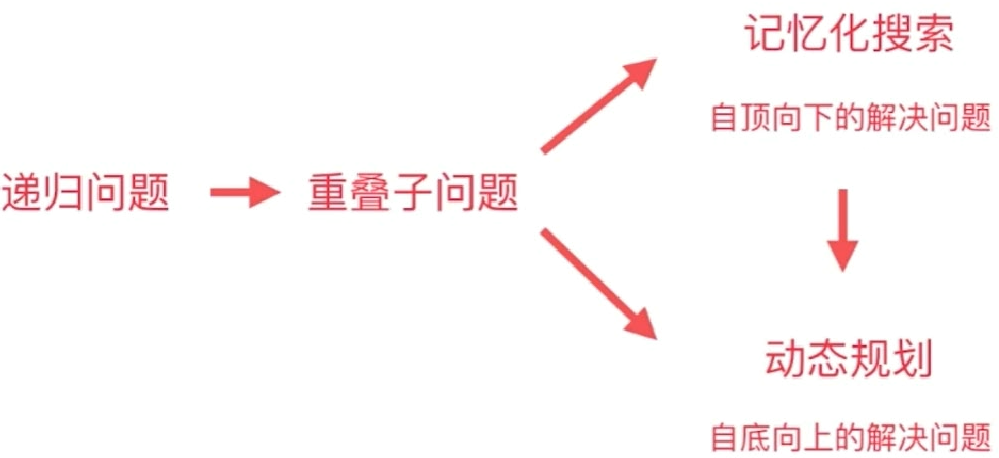
大多数动态规划都是递归问题，但是在这个过程中会发现一些重叠子问题，对于这种子问题一般有两种处理方法：

  1. 记忆法搜索：自顶向下
  2. 动态规划：自底向上

动态规划问题

  • 严格来说应该是拥有重叠子问题和最优子结构才能用动态规划和记忆法搜索
  • 一般来说是先写出记忆化搜索，再来写动态规划，这种方式会简单一些

基本问题

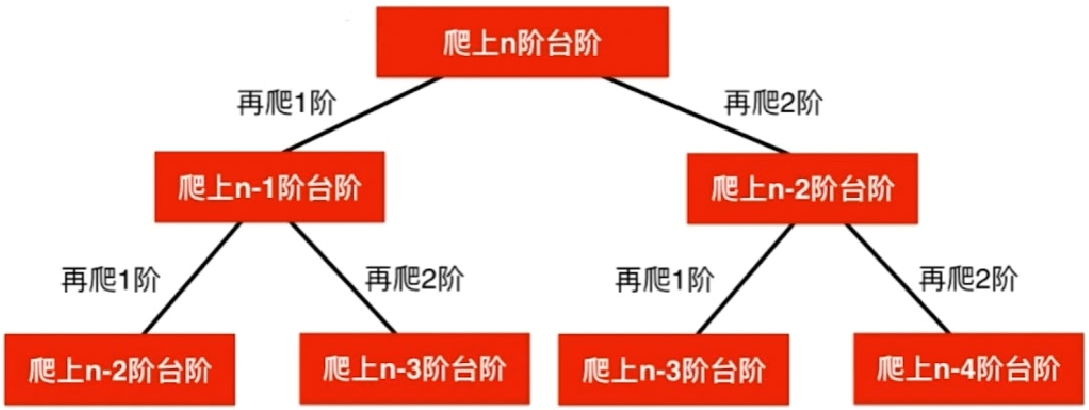
70. 爬楼梯：假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

1
2
3
4
5
输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

1
2
3
4
5
6
输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

思路：

递归树

解题：

记忆法搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/// 记忆化搜索
/// 时间复杂度: O(n)
/// 空间复杂度: O(n)
class Solution {
private:
    vector<int> memo;//记忆数组

    int calcWays(int n){
        if(n == 0 || n == 1)//不走 或 只走一级台阶
            return 1;

        if(memo[n] == -1)//没有保存就记住
            memo[n] = calcWays(n - 1) + calcWays(n - 2);//递归求解

        return memo[n];
    }
public:
    int climbStairs(int n) {
        memo = vector<int>(n + 1, -1);
        return calcWays(n);
    }
};

动态规划：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/// 动态规划
/// 时间复杂度: O(n)
/// 空间复杂度: O(n)
class Solution {
public:
    int climbStairs(int n) {
        vector<int> memo(n + 1, -1);
        memo[0] = 1;
        memo[1] = 1;
        for(int i = 2 ; i <= n ; i ++)
            memo[i] = memo[i - 1] + memo[i - 2];
        return memo[n];
    }
};

相似题目：120. 三角形最小路径和、64. 最小路径和

重叠子问题

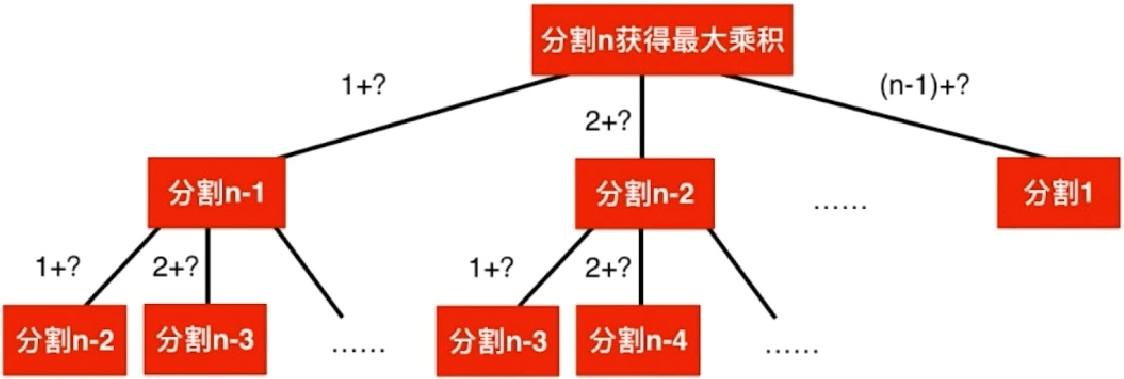
343. 整数拆分：给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:

1
2
3
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

1
2
3
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

说明: 你可以假设 n 不小于 2 且不大于 58。

思路：

递归树

  • 存在大量重复的子结构
  • 子结构中存在最优解

解题：

记忆化搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/// 记忆化搜索
/// 时间复杂度: O(n^2)
/// 空间复杂度: O(n)
class Solution {
private:
    vector<int> memo;

    int max3(int a, int b, int c){
        return max(a, max(b, c));
    }

    // 将n进行分割(至少分割两部分), 可以获得的最大乘积
    int breakInteger(int n){
        if(n == 1)
            return 1;

        if(memo[n] != -1)//有记录 直接返回
            return memo[n];

        int res = -1;
        for(int i = 1 ; i <= n - 1 ; i ++)
            res = max3(res, i * (n - i) , i * breakInteger(n - i));//取3个数中最大值
        memo[n] = res;
        return res;
    }

public:
    int integerBreak(int n) {
        assert(n >= 1);
        memo.clear();
        for(int i = 0 ; i < n + 1 ; i ++)
            memo.push_back(-1);
        return breakInteger(n);
    }
};
  • 注意递归时是i * breakInteger(n - i)而非breakInteger(i) * breakInteger(n - i)，这里i主要是当前拆分的数字，所以用不着对i进行递归

动态规划：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/// 动态规划
/// 时间复杂度: O(n^2)
/// 空间复杂度: O(n)
class Solution {
private:
    int max3(int a, int b, int c ){
        return max(max(a, b), c);
    }

public:
    int integerBreak(int n) {
        assert(n >= 1);
        // memo[i] 表示将数字i分割(至少分割成两部分)后得到的最大乘积
        vector<int> memo(n + 1, -1);

        memo[1] = 1;
        for(int i = 2 ; i <= n ; i ++)
            // 求解memo[i]
            for(int j = 1 ; j <= i - 1 ; j ++)//尝试将memo[i]进行分割
                memo[i] = max3(memo[i], j * (i - j), j * memo[i - j]);//分割两部分或者多部分

        return memo[n];
    }
};

  • 这道题可以用贪心算法，目标为：当长度>=5时，尽可能截取长度为3的：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    /// 贪心算法
    /// 时间复杂度: O(n)
    /// 空间复杂度: O(1)
    class Solution {
    public:
        int integerBreak(int n) {
            if(n == 2)
                return 1;
            else if(n == 3)
                return 2;
            else if(n == 4)
                return 4;
            
            long long sum = 1;
            while(n >= 5)
            {
                sum *= 3;
                sum %= 1000000007;
                n -= 3;
            }
            sum *= n;
            sum %= 1000000007;
            return sum;
        }
    };
    • 该方法的另一个好处是：在动态规划中，当n过大时，在求max时会因为溢出而导致无法将两个数进行比较（溢出数与正常数无法比较）

相似题目：279. 完全平方数（[图的最短路径](# 图的最短路径)是另一种实现方法）、91. 解码方法、62. 不同路径、63. 不同路径 II

状态的定义和状态转移

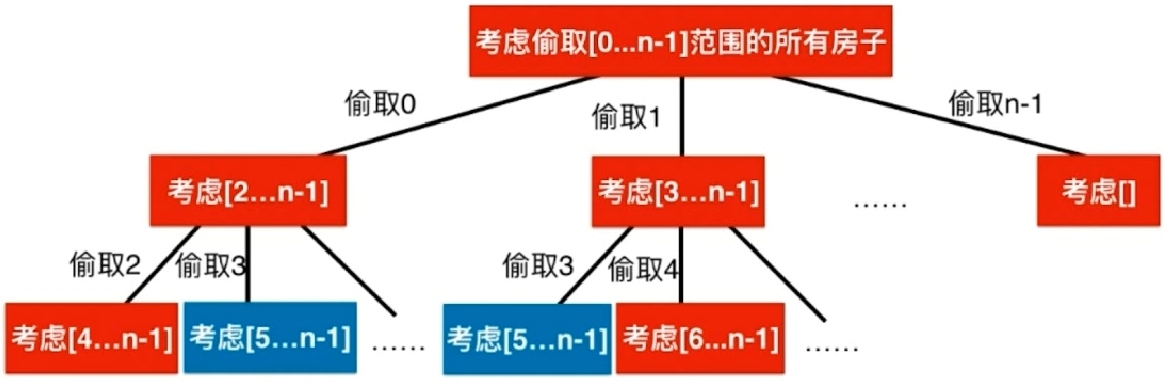
198. 打家劫舍：你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

1
2
3
4
输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

1
2
3
4
输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示：

  • 0 <= nums.length <= 100
  • 0 <= nums[i] <= 400

思路：

递归树

解题：

假设其状态f(x)f(x)为：偷取[x,...,n−1][x,...,n-1]范围中的房子，则有状态转移方程：

f(0)=max(v(0)+f(2),v(1)+f(3),v(2)+f(4),...,v(n−3)+f(n−1),v(n−2),v(n−1))f(0)=max(v(0)+f(2),v(1)+f(3),v(2)+f(4),...,v(n-3)+f(n-1),v(n-2),v(n-1))

其中v(x)v(x)为x房间的金额

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/// 动态规划
/// 时间复杂度: O(n^2)
/// 空间复杂度: O(n)
class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if(n == 0)
            return 0;

        // memo[i] 表示考虑抢劫 nums[i...n) 所能获得的最大收益 memo[x] --> f(x)
        vector<int> memo(n, 0);
        memo[n - 1] = nums[n - 1];//从最后开始偷取 nums[x] --> v(x)
        for(int i = n - 2 ; i >= 0 ; i --)
            for (int j = i; j < n; j++)
                memo[i] = max(memo[i],
                              nums[j] + (j + 2 < n ? memo[j + 2] : 0));//状态转移方程

        return memo[0];
    }
};

假设其状态f(x)f(x)为：偷取[0,...,x][0,...,x]范围中的房子，则有状态转移方程：

f(x)=max(v(x)+f(x−2),v(x−1)+f(x−3),...,v(3)+f(1),v(2),v(1))f(x)=max(v(x)+f(x-2),v(x-1)+f(x-3),...,v(3)+f(1),v(2),v(1))

其中v(x)v(x)为x房间的金额

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if( n == 0 )
            return 0;

        // memo[i] 表示考虑抢劫 nums[0...i] 所能获得的最大收益 memo[x] --> f(x)
        vector<int> memo(n, 0);
        memo[0] = nums[0];//nums[x] --> v(x)
        for(int i = 1 ; i < n ; i ++)
            for (int j = i; j >= 0; j--)
                memo[i] = max(memo[i],
                              nums[j] + (j - 2 >= 0 ? memo[j - 2] : 0));

        return memo[n-1];
    }
};

相似题目：213. 打家劫舍 II、337. 打家劫舍 III、309. 最佳买卖股票时机含冷冻期

0-1背包问题

有一个背包，它的容量为C。现在有n种不同的物品，编号为0…n-1，其中每一件物品的重量为w(i)，价值为v(i)。问可以向这个背包中盛放哪些物品，使得在不超过背包容量的基础上，物品的总价值最大。

注意：贪心算法这里容易陷入局部最优解

假设其状态f(n,C)f(n,C)为：将n个物品放进容量为C的背包，使得价值最大（两个状态，所以后文需要一个表格来辅助）。则有状态转移方程：

f(i,c)=max(f(i−1,c),v(i)+f(i−1,c−w(i)))f(i,c)=max(f(i-1,c),v(i)+f(i-1,c-w(i)))

其中：

  • f(i,c)f(i,c)为将i个物品放入容量为c的背包中并使得价值最大
  • v(i)v(i)为第i个物品的价值
  • w(i)w(i)为第i个物品的重量

求解：

记忆化搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/// 时间复杂度: O(n * C) 其中n为物品个数; C为背包容积
/// 空间复杂度: O(n * C)
class Knapsack01{
private:
    vector<vector<int>> memo;

    // 用 [0...index]的物品,填充容积为c的背包的最大价值
    int bestValue(const vector<int> &w, const vector<int> &v, int index, int c){
        if(c <= 0 || index < 0)
            return 0;

        if(memo[index][c] != -1)//如果之前有存储
            return memo[index][c];
        //不考虑index的物品
        int res = bestValue(w, v, index-1, c);
        //考虑index的物品
        if(c >= w[index])
            res = max(res, v[index] + bestValue(w, v, index - 1, c - w[index]));
        memo[index][c] = res;//存储 以便之后使用
        return res;
    }

public:
    //w：重量 v：价值 C：背包容量
    int knapsack01(const vector<int> &w, const vector<int> &v, int C){
        assert(w.size() == v.size() && C >= 0);
        int n = w.size();
        if(n == 0 || C == 0)
            return 0;

        memo.clear();
        for(int i = 0 ; i < n ; i ++)
            memo.push_back(vector<int>(C + 1, -1));
        return bestValue(w, v, n - 1, C);
    }
};

动态规划：

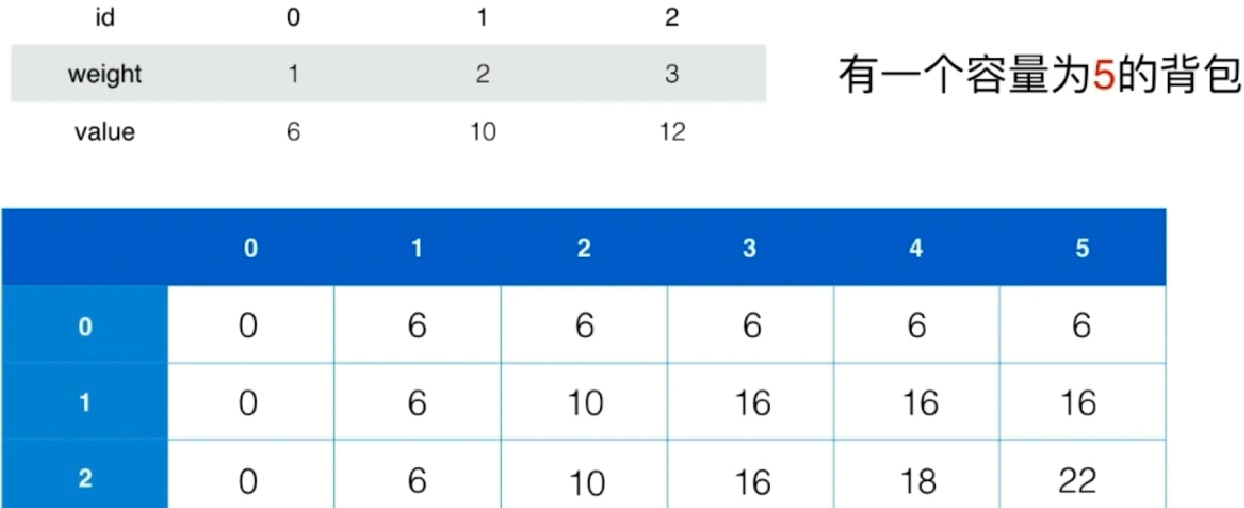
动态规划表——变量memo

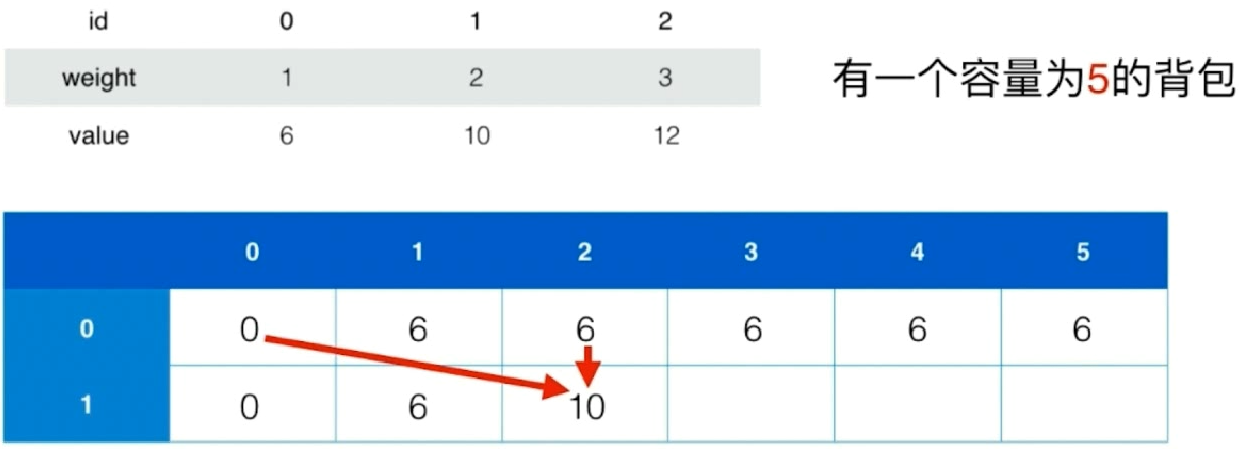
  • 总共三种类型的物体，id分别为0、1、2
  • 表格从上至下，从左至右填充
  • 每行为最多可放入的物体id
  • 每列为假设的背包大小
  • 最终的最大值一定在右下角
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/// 时间复杂度: O(n * C) 其中n为物品个数; C为背包容积
/// 空间复杂度: O(n * C)
class Knapsack01{
public:
    //w：重量 v：价值 C：背包容量
    int knapsack01(const vector<int> &w, const vector<int> &v, int C){
        assert(w.size() == v.size() && C >= 0);
        int n = w.size();
        if(n == 0 || C == 0)
            return 0;

        vector<vector<int>> memo(n, vector<int>(C + 1,0));//n行 C+1列（即上述表格）
        //初始化第一行（先放入第一个物品重量为w[0],价值为v[0]）
        for(int j = 0 ; j <= C ; j ++)//j为背包容量
            memo[0][j] = (j >= w[0] ? v[0] : 0 );
        //填充剩下所有行
        for(int i = 1 ; i < n ; i ++)
            for(int j = 0 ; j <= C ; j ++){
                memo[i][j] = memo[i-1][j];//直接不考虑当前物品w[i] 所以当前值==上一行的值
                if(j >= w[i])//背包容量能够装下当前物品w[i]
                    memo[i][j] = max(memo[i][j], v[i] + memo[i - 1][j - w[i]]);//比较当前值（不考虑当前物品）和考虑放入当前物品的值
            }
        return memo[n - 1][C];
    }
};

优化——缩减空间

回顾其状态转移方程，发现其状态之和上一次的状态有关，理论上的状态转移表最多只需要两行即可（滚动数组），故可以将空间复杂度从O(nC)O(nC)降到O(2C)O(2C)即O(C)O(C)

关于滚动数组，可以发现第一行永远是处理i为偶数时（i从0开始，i为上述表中的行号）的情况，而第二行永远在处理i为奇数的情况

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/// 时间复杂度: O(n * C) 其中n为物品个数; C为背包容积
/// 空间复杂度: O(C), 实际使用了2*C的额外空间
class Knapsack01{
public:
    int knapsack01(const vector<int> &w, const vector<int> &v, int C){
        assert(w.size() == v.size() && C >= 0);
        int n = w.size();
        if( n == 0 && C == 0 )
            return 0;

        vector<vector<int>> memo(2, vector<int>(C + 1, 0));//缩减到2行
        //初始化第一行（先放入第一个物品重量为w[0],价值为v[0]）
        for(int j = 0 ; j <= C ; j ++)
            memo[0][j] = (j >= w[0] ? v[0] : 0);
        //填充剩下所有行
        for(int i = 1 ; i < n ; i ++)
            for(int j = 0 ; j <= C ; j ++){
                memo[i % 2][j] = memo[(i-1) % 2][j];//第二行 i应该且偶数 之后的行会自动滚动
                if(j >= w[i])
                    memo[i % 2][j] = max(memo[i % 2][j], v[i] + memo[(i-1) % 2][j - w[i]]);//和之前比仅仅只增加了 %2
            }
        return memo[(n-1) % 2][C];//同样需要 %2
    }
};

通过下图可以看出：

永远只使用左边、上边的元素

当前行永远只会使用左边以及上方的元素，所以可以从右边进行更新表格，从而使得只占用一行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/// 时间复杂度: O(n * C) 其中n为物品个数; C为背包容积
/// 空间复杂度: O(C), 只使用了C的额外空间
class Knapsack01{
public:
    int knapsack01(const vector<int> &w, const vector<int> &v, int C){
        assert(w.size() == v.size() && C >= 0);
        intn = w.size();
        if(n == 0 || C == 0)
            return 0;

        vector<int> memo(C+1,0);//只是用一行
        //初始化第一行（先放入第一个物品重量为w[0],价值为v[0]）
        for(int j = 0 ; j <= C ; j ++)
            memo[j] = (j >= w[0] ? v[0] : 0);

        for(int i = 1 ; i < n ; i ++)
            for(int j = C ; j >= w[i] ; j --)//从右往左更新，且背包容量至少需要w[i]才能装入i物体
                memo[j] = max(memo[j], v[i] + memo[j - w[i]]);//max(不放i物体,放入i物体)

        return memo[C];
    }
};

变体

  • 完全背包问题：每个物体可以无限使用
    • 可以根据背包容量来判断每个物体最大的数量，从而转化为标准问题
  • 多重背包问题：每个物体不止1个，有num(i)个
  • 多维费用背包问题：要考虑物品的体积和重量两个维度
  • 物品间加入更多约束：物品间可以互相排斥；也可以互相依赖

leetcode中的问题

416. 分割等和子集：给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:

  1. 每个数组中的元素不会超过 100
  2. 数组的大小不会超过 200

示例 1:

1
2
3
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:

1
2
3
输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.

思路：

典型背包问题：在n个物品中选出一定物品，完全填满sum/2的背包

假设其状态f(n,C)f(n,C)为：将n个物品放进容量为C的背包使其刚好填满。则有状态转移方程：

f(i,c)=f(i−1,c)∣∣f(i−1,c−w(i))f(i,c)=f(i-1,c)||f(i-1,c-w(i))

其中：

  • f(i,c)f(i,c)为将i个物品放入容量为c的背包中
  • w(i)w(i)为第i个物品的大小

解题：

记忆化搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/// 时间复杂度: O(len(nums) * O(sum(nums)))
/// 空间复杂度: O(len(nums) * O(sum(nums)))
class Solution {
private:
    // memo[i][c] 表示使用索引为[0...i]的这些元素,是否可以完全填充一个容量为c的背包
    // -1 表示为未计算; 0 表示不可以填充; 1 表示可以填充
    vector<vector<int>> memo;

    // 使用nums[0...index], 是否可以完全填充一个容量为sum的背包
    bool tryPartition(const vector<int> &nums, int index, int sum){
        if(sum == 0)
            return true;
        if(sum < 0 || index < 0)
            return false;

        if(memo[index][sum] != -1)
            return memo[index][sum] == 1;

        memo[index][sum] = ( tryPartition(nums, index - 1, sum) ||//不用index处的物体填充
               tryPartition(nums, index - 1, sum - nums[index]) ) ? 1 : 0;//使用index处的物体填充

        return memo[index][sum] == 1;
    }

public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(int i = 0 ; i < nums.size() ; i ++){
            assert(nums[i] > 0);
            sum += nums[i];
        }
        if(sum % 2)//总和需要能够平分
            return false;

        memo.clear();
        for(int i = 0 ; i < nums.size() ; i ++)
            memo.push_back(vector<int>(sum / 2 + 1, -1));
        return tryPartition(nums, nums.size() - 1, sum / 2);
    }
};

动态规划：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/// 时间复杂度: O(len(nums) * O(sum(nums)))
/// 空间复杂度: O(len(nums) * O(sum(nums)))
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(int i = 0 ; i < nums.size() ; i ++){
            assert(nums[i] > 0);
            sum += nums[i];
        }
        if(sum % 2)//总和需要能够平分
            return false;

        int n = nums.size();
        int C = sum / 2;
        vector<bool> memo(C + 1, false);//只需要一行即可
        for(int i = 0 ; i <= C ; i ++)
            memo[i] = (nums[0] == i);//初始填充（只有当背包容量==第一个物体大小的时候才能填满）

        for(int i = 1 ; i < n ; i ++)//填充剩下行（即考虑剩下物品）
            for(int j = C; j >= nums[i] ; j --)//由于memo只有一行 所以要从后向前推
                memo[j] = memo[j] || memo[j - nums[i]];//考虑未放当前物品背包情况memo[i]和放入当前物品背包情况memo[j-nums[i]],是否能够填满背包

        return memo[C];//最后一个值即为是否能够填满背包
    }
};

相似题目：322. 零钱兑换、377. 组合总和 Ⅳ、474. 一和零、139. 单词拆分、494. 目标和

最长上升子序列问题（LIS）

300. 最长递增子序列：给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

1
2
3
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

1
2
输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

1
2
输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

  • 1 <= nums.length <= 2500
  • −104<=nums[i]<=104-10^4 <= nums[i] <= 10^4

进阶：

  • 你可以设计时间复杂度为 O(n2)O(n^2) 的解决方案吗？
  • 你能将算法的时间复杂度降低到 O(nlog(n))O(n log(n)) 吗?

思路：

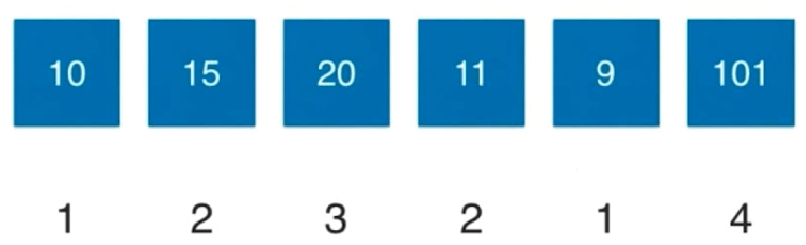
假设LIS(i)：表示以第i个数字为结尾的最长上升子序列的长度

状态：LIS(i)表示[0...i][0...i]的范围内，选择数字nums[i]可以获得的最长上升子序列的长度

状态转移方程：LIS(i)=max⁡j<i{1+LIS(j)if(nums[i]>nums[j])}LIS(i)=\max_{j<i}\left \{1+LIS(j) if (nums[i]>nums[j])\right \}

例子

  • 下方数字即为最长上升子序列长度，即下面的memo变量
  • 默认初始值均为1，表示初始最长上升子序列长度为1
  • 从左至右遍历memo，发现之前有memo值比当前值大且满足上升子序列规则，则进行更新并+1

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/// 时间复杂度: O(n^2)
/// 空间复杂度: O(n)
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.size() == 0)
            return 0;

        // memo[i] 表示以 nums[i] 为结尾的最长上升子序列的长度
        vector<int> memo(nums.size(), 1);//全部初始化为1 即默认最长序列为1
        for(int i = 1 ; i < nums.size() ; i ++)//遍历memo 寻找并填充最长序列
            for(int j = 0 ; j < i ; j ++)//遍历memo之前序列[0,i-1]
                if(nums[i] > nums[j])//如果当前值nums[i]和之前值能构成序列
                    memo[i] = max(memo[i], 1 + memo[j]);//如果nums[i]之前存在能构成序列的数，尝试+1 看是否是最大值
        //遍历求出memo中的最大值 即为最长上升子序列长度
        int res = memo[0];
        for(int i = 1 ; i < nums.size() ; i ++)
            res = max(res, memo[i]);

        return res;
    }
};

相似题目：376. 摆动序列

如果需要得到对应的子序列，则需要从最大的memo向左寻找第二大的memo并记录该memo值对应的原始数据，反复上述查找过程并记录对应的原始数据，可以得到最终的原始子序列

更多问题

最长公共子序列（LCS）

给出两个字符串S1和S2，求这两个字符串的最长公共子序列的长度

状态：LCS(m,n)表示S1[0...m]S1[0...m]和S2[0...n]S2[0...n]的最长公共子序列的长度

状态转移方程：

LCS(m,n)={1+LCS(m−1,n−1),s1[m]=s2[n]max{LCS(m−1,n),LCS(m,n−1)},s1[m]!=s2[n]LCS(m,n)=\begin{cases} & 1+LCS(m-1,n-1) &,s1[m]=s2[n] \\ & max \left \{ LCS(m-1,n),LCS(m,n-1) \right \} &,s1[m]!=s2[n] \end{cases}

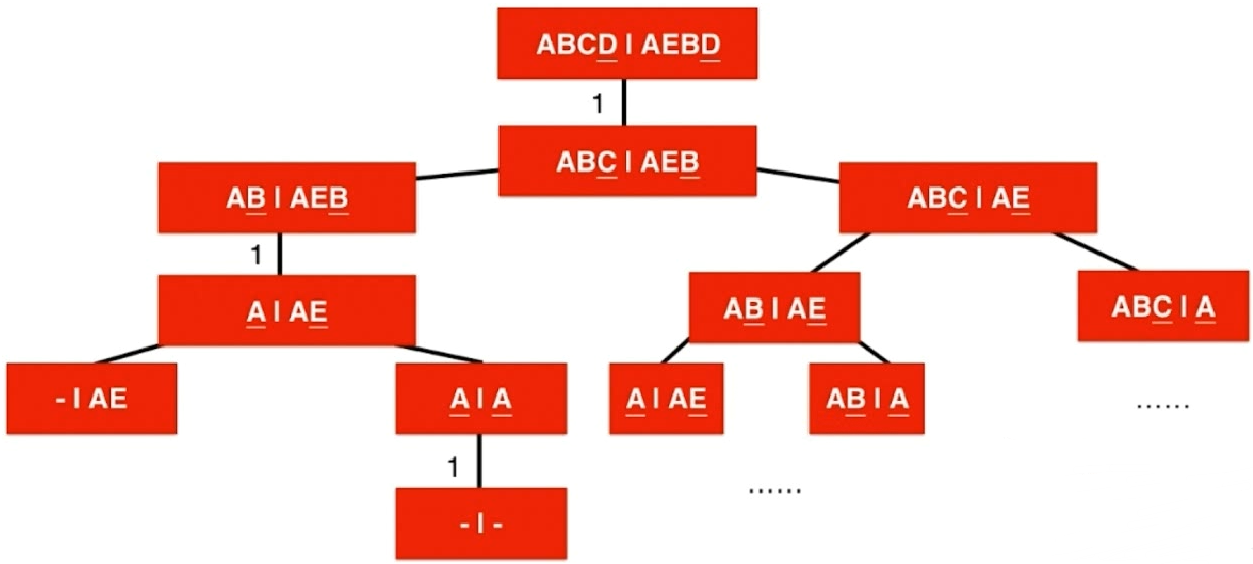
假设字符串ABCD和AEBD，其最长公共子序列为ABD，其递归树如下：

递归树

解题：

记忆化搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/// 时间复杂度: O(len(s1)*len(s2))
/// 空间复杂度: O(len(s1)*len(s2))
class LCS{
private:
    vector<vector<int> > memo;
    // 求s1[0...m]和s2[0...n]的最长公共子序列的长度值
    int __LCS(const string &s1, const string &s2, int m, int n){
        if(m < 0 || n < 0)
            return 0;
        if(memo[m][n] != -1)
            return memo[m][n];

        int res = 0;
        if(s1[m] == s2[n])
            res = 1 + __LCS(s1, s2, m - 1, n - 1);
        else
            res = max(__LCS(s1, s2, m - 1, n),
                      __LCS(s1, s2, m, n - 1));
        memo[m][n] = res;
        return res;
    }

    // 通过memo反向求解s1和s2的最长公共子序列
    string __getLCS(const string &s1, const string &s2){
        int m = s1.size() - 1;
        int n = s2.size() - 1;

        string res = "";
        while(m >= 0 && n >= 0)
            if(s1[m] == s2[n]){
                res = s1[m] + res;
                m --;
                n --;
            }
            else if(m == 0)
                n --;
            else if(n == 0)
                m --;
            else{
                if(memo[m-1][n] > memo[m][n-1])
                    m --;
                else
                    n --;
            }

        return res;
    }
public:
    string getLCS(const string &s1, const string &s2){
        memo.clear();
        for(int i = 0 ; i < s1.size() ; i ++)
            memo.push_back(vector<int>(s2.size(), -1));

        __LCS(s1, s2, s1.size() - 1, s2.size() - 1);
        return __getLCS(s1, s2);
    }
};

动态规划：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/// 时间复杂度: O(len(s1)*len(s2))
/// 空间复杂度: O(len(s1)*len(s2))
class LCS{
public:
    string getLCS(const string &s1, const string &s2){
        int m = s1.size();
        int n = s2.size();
        // 对memo的第0行和第0列进行初始化
        vector<vector<int> > memo(m, vector<int>(n, 0));
        for(int j = 0 ; j < n ; j ++)
            if(s1[0] == s2[j]){
                for(int k = j ; k < n ; k ++)
                    memo[0][k] = 1;
                break;
            }

        for(int i = 0 ; i < m ; i ++)
            if(s1[i] == s2[0]){
                for(int k = i ; k < m ; k ++)
                    memo[k][0] = 1;
                break;
            }

        // 动态规划的过程
        for(int i = 1 ; i < m ; i ++)
            for(int j = 1 ; j < n ; j ++)
                if(s1[i] == s2[j])
                    memo[i][j] = 1 + memo[i-1][j-1];
                else
                    memo[i][j] = max(memo[i-1][j], memo[i][j-1]);

        // 通过memo反向求解s1和s2的最长公共子序列
        m = s1.size() - 1;
        n = s2.size() - 1;
        string res = "";
        while(m >= 0 && n >= 0)
            if( s1[m] == s2[n] ){
                res = s1[m] + res;
                m --;
                n --;
            }
            else if(m == 0)
                n --;
            else if(n == 0)
                m --;
            else{
                if(memo[m-1][n] > memo[m][n-1])
                    m --;
                else
                    n --;
            }

        return res;
    }
};

dijkstra单源最短路径

状态：shortestPath(i)表示从start到i的最短路径长度

状态转移方程：

shortestPath(x)=min{shortestPath(a)+w(a→x)}shortestPath(x)=min \left \{ shortestPath(a) + w(a \to x) \right \}

其中：

  • w(a→x)w(a \to x)为a到x的权值

详见另一篇文章数据结构与算法中的第八章——最短路径

总结和感悟

  1. 动态规划有时候不能直接根据题目问题设置状态，可以设置一个中间的状态，然后根据该状态求出最后的问题。如下面的题：

九、贪心算法

基础问题

455. 分发饼干：假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

1
2
3
4
5
6
输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:

1
2
3
4
5
6
输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

提示：

  • 1<=g.length<=3∗1041 <= g.length <= 3 * 10^4
  • 0<=s.length<=3∗1040 <= s.length <= 3 * 10^4
  • 1<=g[i],s[j]<=231−11 <= g[i], s[j] <= 2^{31} - 1

思路：将最大的饼干给最大胃口的孩子，通过判断是否满足来决定剩下的分配策略

注意：一般来说需要将s和g进行排序来获得最大的饼干和最大胃口的孩子

一般来说贪心算法需要牵扯带最大最小值，所以一般都需要和排序挂钩

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/// 先尝试满足最贪心的小朋友
/// 时间复杂度: O(nlogn)（主要是排序）
/// 空间复杂度: O(1)
class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(), g.end(), greater<int>());//排序 从大到小排序
        sort(s.begin(), s.end(), greater<int>());

        int gi = 0, si = 0;
        int res = 0;
        while(gi < g.size() && si < s.size()){
            if(s[si] >= g[gi]){//最大饼干满足最大胃口孩子
                res ++;
                si ++;
                gi ++;
            }
            else
                gi ++;//满足不了 直接放弃该孩子
        }

        return res;
    }
};

相似题目：392. 判断子序列

贪心算法与动态规划的关系

435. 无重叠区间：给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

  1. 可以认为区间的终点总是大于它的起点。
  2. 区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

示例 1:

1
2
3
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

1
2
3
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:

1
2
3
输入: [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

思路：

  1. 动态规划：对于每个区间，都可以看其之前的区间，如果可以跟在前面区间的后面，则最大不重叠区间数+1（类似于最长上升子序列，这里需要先排序才能判断是否重叠）
  2. 贪心算法：前面区间结束越早，留给后面的空间就越大，就越有可能插入更多的区间

实现：

动态规划：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/// Definition for an interval.
struct Interval {
    int start;
    int end;
    Interval() : start(0), end(0) {}
    Interval(int s, int e) : start(s), end(e) {}
};

bool compare(const Interval &a, const Interval &b){
    if(a.start != b.start)
        return a.start < b.start;
    return a.end < b.end;
}

/// 动态规划
/// 时间复杂度: O(n^2)
/// 空间复杂度: O(n)
class Solution {
public:
    int eraseOverlapIntervals(vector<Interval>& intervals) {
        if(intervals.size() == 0)
            return 0;

        sort(intervals.begin(), intervals.end(), compare);//区间从小到大排序

        // memo[i]表示以intervals[i]为结尾的区间能构成的最长不重叠区间序列
        vector<int> memo(intervals.size(), 1);
        for(int i = 1 ; i < intervals.size() ; i ++)//从1开始计算后面区间是否重叠
            // 求memo[i]，看前面区间
            for(int j = 0 ; j < i ; j ++)
                if(intervals[i].start >= intervals[j].end)//当前区间在前面区间后
                    memo[i] = max(memo[i], 1 + memo[j]);
        //取出最大memo，即为最长连续区间
        int res = 0;
        for(int i = 0; i < memo.size() ; i ++)
            res = max(res, memo[i]);

        return intervals.size() - res;//放回最短删除区间
    }
};

贪心算法：

按照区间结尾排序，每次选择结尾最早的，且和前一个区间不重叠的区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/// Definition for an interval.
struct Interval {
    int start;
    int end;
    Interval() : start(0), end(0) {}
    Interval(int s, int e) : start(s), end(e) {}
};

bool compare(const Interval &a, const Interval &b){
    if(a.end != b.end)//谁结束的越早 谁排在越前面
        return a.end < b.end;
    return a.start < b.start;
}

/// 时间复杂度: O(n)
/// 空间复杂度: O(n)
class Solution {
public:
    int eraseOverlapIntervals(vector<Interval>& intervals) {
        if(intervals.size() == 0)
            return 0;

        sort(intervals.begin(), intervals.end(), compare);//谁结束的越早 谁排在越前面

        int res = 1;//最多无重复区间数量
        int pre = 0;
        for(int i = 1 ; i < intervals.size() ; i ++)
            if(intervals[i].start >= intervals[pre].end){//后一个区间在前一个区间后
                res ++;
                pre = i;
            }

        return intervals.size() - res;//删除最小区间数量
    }
};

贪心选择性质

贪心选择性质：在求解一个最优化的问题中，采用贪心算法选择一个方式后，不会影响其他子问题的求解

如果无法使用贪心算法，举出反例即可

证明贪心算法对某道题的正确性：数学归纳法、反证法（一般常用反证法）