一、基础排序

对于排序这个问题来说，最优的时间复杂度在O(N∗logN)O(N*logN)级别的

常用排序算法时间复杂度：

排序算法 平均时间复杂度 原地排序 空间复杂度 稳定性
冒泡排序 O(n2)O(n^2) O(1)O(1) √
选择排序 O(n2)O(n^2) O(1)O(1) ×
插入排序 O(n2)O(n^2) √ O(1)O(1) √
希尔排序 O(n3/2)O(n^{3/2}) O(1)O(1) ×
快速排序 O(N∗logN)O(N*logN) √ O(nlog2n)O(nlog_2n) ×
归并排序 O(N∗logN)O(N*logN) × O(n)O(n) √
堆排序 O(N∗logN)O(N*logN) √ O(1)O(1) ×
基数排序 O(n∗k)O(n*k) O(n+k)O(n+k) √

稳定排序：对于相等的元素，在排序后，这几个相等元素中原来靠前的元素依然靠前。即，相等元素的相对位置没有发生改变。

  • 可以通过自定义比较函数，让排序算法不存在稳定性的问题

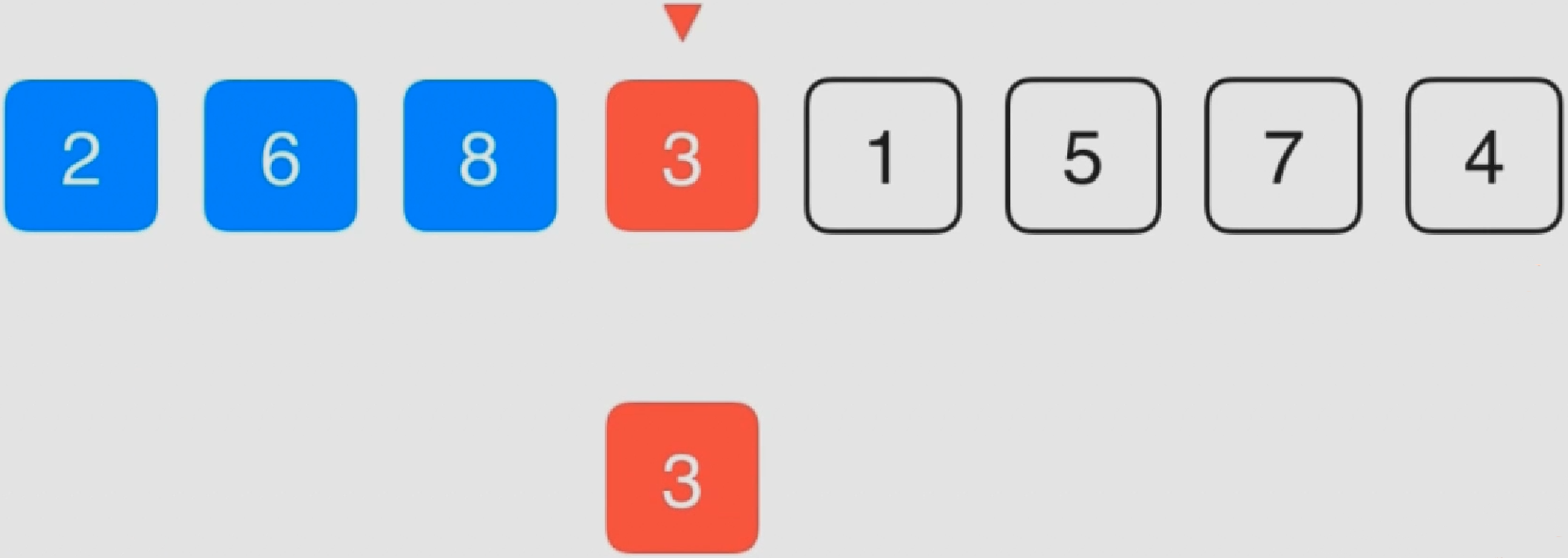
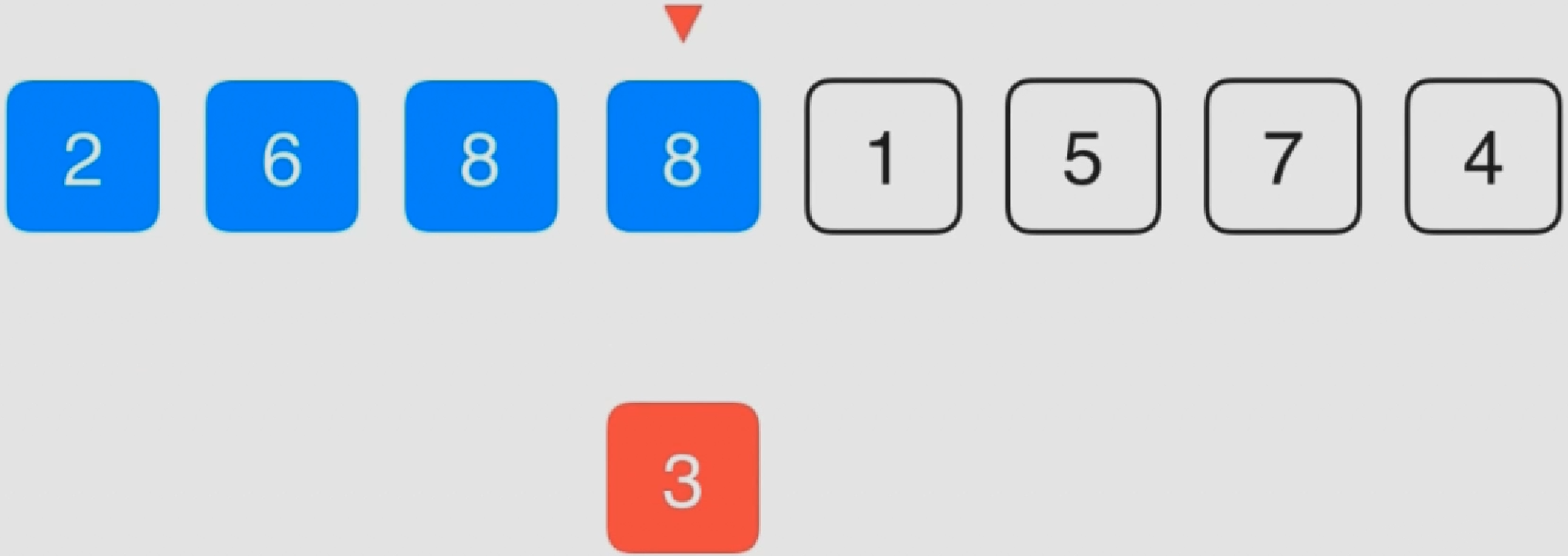
0.冒泡排序

该算法重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

该算法每次遍历都将最大的元素放到了最后（默认从小到大排序）

步骤：

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

动图演示

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
template<typename T>
void bubbleSort( T arr[] , int n){
    bool swapped;
    do{
        swapped = false;
        for( int i = 1 ; i < n ; i ++ )
            if( arr[i-1] > arr[i] ){
                swap( arr[i-1] , arr[i] );
                swapped = true;
            }
        
        // 优化, 每一趟Bubble Sort都将最大的元素放在了最后的位置
        // 所以下一次排序, 最后的元素可以不再考虑
        n --;
    }while(swapped);
}

优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template<typename T>
void bubbleSort2( T arr[] , int n){
    int newn; // 使用newn进行优化
    do{
        newn = 0;
        for( int i = 1 ; i < n ; i ++ )
            if( arr[i-1] > arr[i] ){
                swap( arr[i-1] , arr[i] );

                // 记录最后一次的交换位置,在此之后的元素在下一轮扫描中均不考虑
                newn = i;
            }
        n = newn;
    }while(newn > 0);
}

1.选择排序

选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。

步骤：

  1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
  2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
  3. 重复第二步，直到所有元素均排序完毕。

动图演示

基本思路（从小到大）：

  1. 找到未排序的整个序列中最小的元素
  2. 与未排序序列中的第一个元素进行交换
  3. 重复上述过程直至结束

选择排序1

选择排序2

  • 2之后最小的元素是3
  • 将3与2号（0号开始）元素进行交换

实现：

1
2
3
4
5
6
7
8
9
10
11
12
template<typename T>
void selectionSort(T arr[], int n){// arr：输入输出数组 n：数组长度
    for(int i = 0 ; i < n ; i ++){

        int minIndex = i;// 当前最小值索引
        for( int j = i + 1 ; j < n ; j ++ )
            if( arr[j] < arr[minIndex] )
                minIndex = j;

        swap( arr[i] , arr[minIndex] );
    }
}
  • 任何情况下，该算法的两层循环都必须全部执行完，所以效率较低

改进

在每一轮中, 可以同时找到当前未处理元素的最大值和最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
template<typename T>
void selectionSort(T arr[], int n){
    int left = 0, right = n - 1;
    while(left < right){
        int minIndex = left;
        int maxIndex = right;

        // 在每一轮查找时, 要保证arr[minIndex] <= arr[maxIndex]
        if(arr[minIndex] > arr[maxIndex])
            swap(arr[minIndex], arr[maxIndex]);

        for(int i = left + 1 ; i < right; i ++)
            if(arr[i] < arr[minIndex])
                minIndex = i;
            else if(arr[i] > arr[maxIndex])
                maxIndex = i;

        swap(arr[left], arr[minIndex]);
        swap(arr[right], arr[maxIndex]);

        left ++;
        right --;
    }
    return;
}

2.插入排序

步骤：

  1. 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
  2. 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

动图演示

基本实现

基本思路（从小到大）：将当前未排序元素放入前面已经排好序的元素中合适的位置（0号元素可以不考虑）

插入排序1

插入排序2

插入排序3

  1. 3比前面元素8小，所以交换位置
  2. 3又比6小，交换位置
  3. 此时位置合适

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template<typename T>
void insertionSort(T arr[], int n){
    for( int i = 1 ; i < n ; i ++ ) {// 0号元素不用考虑

        // 寻找元素arr[i]合适的插入位置
        // 写法1
//        for( int j = i ; j > 0 ; j-- )
//            if( arr[j] < arr[j-1] )
//                swap( arr[j] , arr[j-1] );
//            else
//                break;

        // 写法2
        for( int j = i ; j > 0 && arr[j] < arr[j-1] ; j -- )
            swap( arr[j] , arr[j-1] );
    }
    return;
}
  • 内层循环可以提前终止，所以插入排序理论上来说比选择排序更快一些
  • 但是该方法交换部分和比较操作来比更为费时（一次交换需要3次赋值），所以导致该算法比之前插入排序费时

优化

优化思路：将之前的多次交换操作变为一次赋值操作

插入排序-优化1

  • 先保存当前要排序的一个副本

插入排序-优化2

  • 比较当前副本和其位置之前的元素8，发现比8小，将8挪到当前3的位置上

插入排序-优化3

  • 假设将副本中的元素放到8的位置，此时需要和8的前一个元素6进行比较，发现比6小，将6移到8的位置上去

插入排序-优化4

  • 再将3放到原来6的位置上去，此时发现3比2大

插入排序-优化5

  • 此时位置正确，放入3

实现：

1
2
3
4
5
6
7
8
9
10
11
12
template<typename T>
void insertionSort(T arr[], int n){
    for( int i = 1 ; i < n ; i ++ ) {
        // 寻找元素arr[i]合适的插入位置
        T e = arr[i];// 保存待排序的元素
        int j; // j保存元素e应该插入的位置
        for (j = i; j > 0 && arr[j-1] > e; j--)
            arr[j] = arr[j-1];// 将前一个元素向后挪动
        arr[j] = e;
    }
    return;
}
  • 此时插入排序效率会比选择排序效率高（会提前终止内层循环，尤其是有重复数据或近乎有序的数据时）
  • 对于一个近乎有序的数据来说，插入排序的效率要远远高于选择排序，此时时间复杂度接近O(n)O(n)

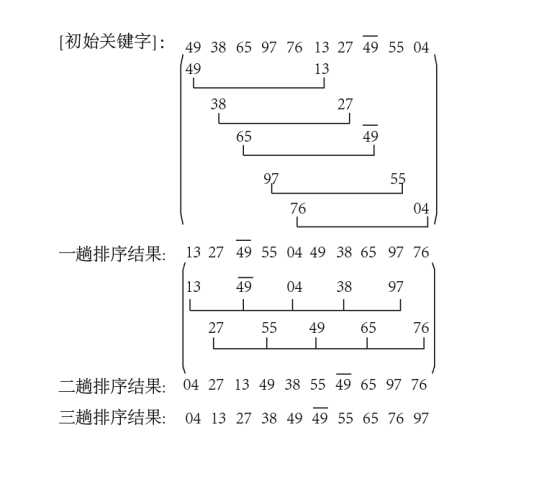
3.希尔排序

希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法

希尔排序是把序列按一定增量h来分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的元素越来越多，当增量减至 1 时，整个序列恰被分成一组，算法便终止。

步骤：

  1. 选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；
  2. 按增量序列个数 k，对序列进行 k 趟排序；
  3. 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

图例：

这里选择增量h=length/2，缩小增量继续以h= h/2的方式，这种增量选择可以用一个序列来表示，{n/2,(n/2)/2…1}，称为增量序列。希尔排序的增量序列的选择与证明是个数学难题，{n/2,(n/2)/2…1}增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。此处示例使用希尔增量

希尔排序

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
template<typename T>
void shellSort(T arr[], int n){

    // 计算 increment sequence: 1, 4, 13, 40, 121, 364, 1093...
    int h = 1;
    while( h < n/3 )
        h = 3 * h + 1;

    while( h >= 1 ){

        // h-sort the array
        for( int i = h ; i < n ; i ++ ){

            // 对 arr[i], arr[i-h], arr[i-2*h], arr[i-3*h]... 使用插入排序
            T e = arr[i];
            int j;
            for( j = i ; j >= h && e < arr[j-h] ; j -= h )
                arr[j] = arr[j-h];
            arr[j] = e;
        }

        h /= 3;
    }
}
  • 该增量序列是最优的序列，此时时间复杂度可以达到O(n3/2)O(n^{3/2})

二、高级排序

该章中的算法时间复杂度均为O(N∗logN)O(N*logN)

1.归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：

  • 自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）；
  • 自下而上的迭代；

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(N∗logN)O(N*logN) 的时间复杂度。代价是需要额外的内存空间，由O(1)O(1)到O(N)O(N)

步骤：

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  4. 重复步骤 3 直到某一指针达到序列尾；
  5. 将另一序列剩下的所有元素直接复制到合并序列尾。

动图演示——迭代

自顶向下——递归

实现：

归并过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
template<typename  T>
void __merge(T arr[], int l, int mid, int r){
    //* VS不支持动态长度数组, 即不能使用 T aux[r-l+1]的方式申请aux的空间
    //* 使用VS的请使用new的方式申请aux空间
    //* 使用new申请空间, 不要忘了在__merge函数的最后 delete 掉申请的空间:)
    T aux[r-l+1];
    //T *aux = new T[r-l+1];

    for( int i = l ; i <= r; i ++ )
        aux[i-l] = arr[i];// 拷贝一份副本

    // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
    int i = l, j = mid+1;
    for( int k = l ; k <= r; k ++ ){//k指向最终的目的地中的索引

        if( i > mid ){  // 如果左半部分元素已经全部处理完毕
            arr[k] = aux[j-l]; j ++;
        }
        else if( j > r ){  // 如果右半部分元素已经全部处理完毕
            arr[k] = aux[i-l]; i ++;
        }
        else if( aux[i-l] < aux[j-l] ) {  // 左半部分所指元素 < 右半部分所指元素
            arr[k] = aux[i-l]; i ++;
        }
        else{  // 左半部分所指元素 >= 右半部分所指元素
            arr[k] = aux[j-l]; j ++;
        }
    }

    //delete[] aux;
}

// 递归使用归并排序,对arr[l...r]的范围进行排序
template<typename T>
void __mergeSort(T arr[], int l, int r){
    if( l >= r )
        return;

    int mid = (l+r)/2;
    __mergeSort(arr, l, mid);//递归排序左半部分
    __mergeSort(arr, mid+1, r);//递归排序右半部分
    __merge(arr, l, mid, r);//归并操作：真正的排序
}

  • 该方法在有序列表中会远远慢于插入算法，但是通过以下优化在一定程度上缓解：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    template<typename T>
    void __mergeSort(T arr[], int l, int r){
        // 优化2: 对于小规模数组, 使用插入排序
        if( r - l <= 15 ){
            insertionSort(arr, l, r);
            return;
        }

        int mid = (l+r)/2;
        __mergeSort(arr, l, mid);
        __mergeSort(arr, mid+1, r);

        // 优化1: 对于arr[mid] <= arr[mid+1]的情况,不进行merge
        // 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
        if( arr[mid] > arr[mid+1] )
            __merge(arr, l, mid, r);
    }

自底向上——迭代

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 使用自底向上的归并排序算法
template <typename T>
void mergeSortBU(T arr[], int n){

    // Merge Sort Bottom Up 无优化版本
//    for( int sz = 1; sz < n ; sz += sz )// 每次归并的最小单位中的元素个数
//        for( int i = 0 ; i < n - sz ; i += sz+sz )// 每次归并两个最小单位，其中i+sz<n保证了后一个最小单位的存在，无论其多长
//            // 对 arr[i...i+sz-1] 和 arr[i+sz...i+2*sz-1] 进行归并
//            __merge(arr, i, i+sz-1, min(i+sz+sz-1,n-1) );// 真正归并，min()是为了防止第二个最小单位过短


    // Merge Sort Bottom Up 优化
    // 对于小数组, 使用插入排序优化
    for( int i = 0 ; i < n ; i += 16 )
        insertionSort(arr,i,min(i+15,n-1));

    for( int sz = 16; sz < n ; sz += sz )
        for( int i = 0 ; i < n - sz ; i += sz+sz )
            // 对于arr[mid] <= arr[mid+1]的情况,不进行merge
            if( arr[i+sz-1] > arr[i+sz] )
                __merge(arr, i, i+sz-1, min(i+sz+sz-1,n-1) );

    // Merge Sort BU 也是一个O(nlogn)复杂度的算法，虽然只使用两重for循环
    // 所以，Merge Sort BU也可以在1秒之内轻松处理100万数量级的数据
    // 注意：不要轻易根据循环层数来判断算法的复杂度，Merge Sort BU就是一个反例
}
  • 该算法中未使用数组的索引特点，所以适合链表使用

性能区别

自底向上（迭代）的归并排序，是比自顶向下（递归）的归并排序要快的

上述两种对归并排序中主要存在两个可以优化的地方：

  • 使用插入排序对小数组进行处理。这个优化对两个算法的作用是相同的
  • 判断两个序列是否需要真正的归并

注意：在自顶向下的归并排序中，后一个优化可以发生在非常高的层次，也就是面对两个很大的数组，可以通过这步优化，使得不需要进一步处理两个大数组！但是在自底向上的归并排序中却不能跨过具有这种性质的大数组。由于这个原因，自底向上的归并排序的速度被拖慢了！

另外，虽然递归调用确实会有额外的开销，但是在现代计算机上，对于最新的C++编译器，对此都会有所优化

2.快速排序

快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法

步骤：

  1. 从数列中挑出一个元素，称为 “基准”（pivot）（一般为第一个元素）
  2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去

动图演示

实现：

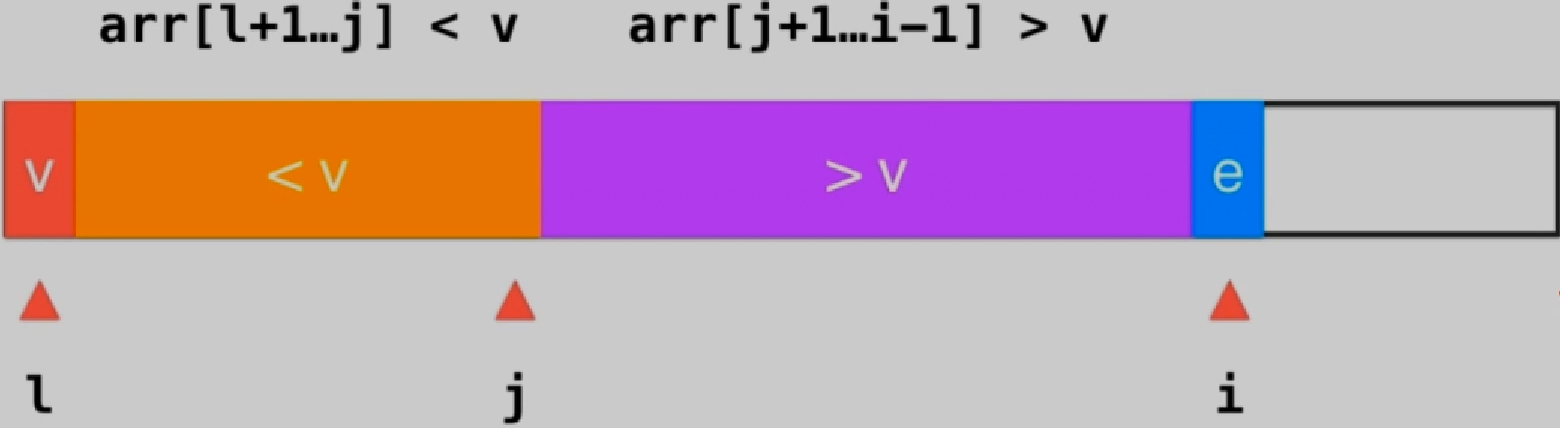
分区(partition)操作

  • 比较i处元素e和v的大小，并将e放到对应位置，之后i++，指向新的元素
    • 如果e>=v，i++（=随便放，默认在右边）
    • 如果e<v，swap(arr[j+1], arr[i])，j++
  • swap(arr[l], arr[j])，此时v放到了合适的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] < arr[p+1...r]
template <typename T>
int __partition(T arr[], int l, int r){
    T v = arr[l];// 标准 v

    // 使得arr[l+1...j] < v < arr[j+1...i)
    int j = l;// 初始化j，此时<v的部分为空
    for( int i = l + 1 ; i <= r ; i ++ )// 初始化i，此时>v的部分为空
        if( arr[i] < v ){// arr[i]>v时，i++
            j ++;
            swap( arr[j] , arr[i] );
        }

    swap( arr[l] , arr[j]);

    return j;// 此时j为v对应的编号
}

// 对arr[l...r]部分进行快速排序
template <typename T>
void __quickSort(T arr[], int l, int r){

    if( l >= r )
        return;

    int p = __partition(arr, l, r);
    __quickSort(arr, l, p-1 );
    __quickSort(arr, p+1, r);
}

局限性与优化

局限性：

  1. 在近乎有序的列表中会导致算法退化为O(n2)O(n^2)
    • 该方式会使算法按照v划分左右两块时极度不平衡而导致算法时间复杂度退化
  2. 在有很多重复数据的列表中会导致算法退化为O(n2)O(n^2)
    • 该方式和上述类似，无论重复数据放左边还是右边均会导致两边极度不平衡

优化：

  1. 采用随即快排：选取标定点v时采用随机的方式

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    // 对arr[l...r]部分进行快速排序
    template <typename T>
    void _quickSort(T arr[], int l, int r){
        // 对于小规模数组, 使用插入排序进行优化
        if( r - l <= 15 ){
            insertionSort(arr,l,r);
            return;
        }

        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap( arr[l] , arr[rand()%(r-l+1)+l] );
        
        int p = _partition(arr, l, r);
        _quickSort(arr, l, p-1 );
        _quickSort(arr, p+1, r);
    }

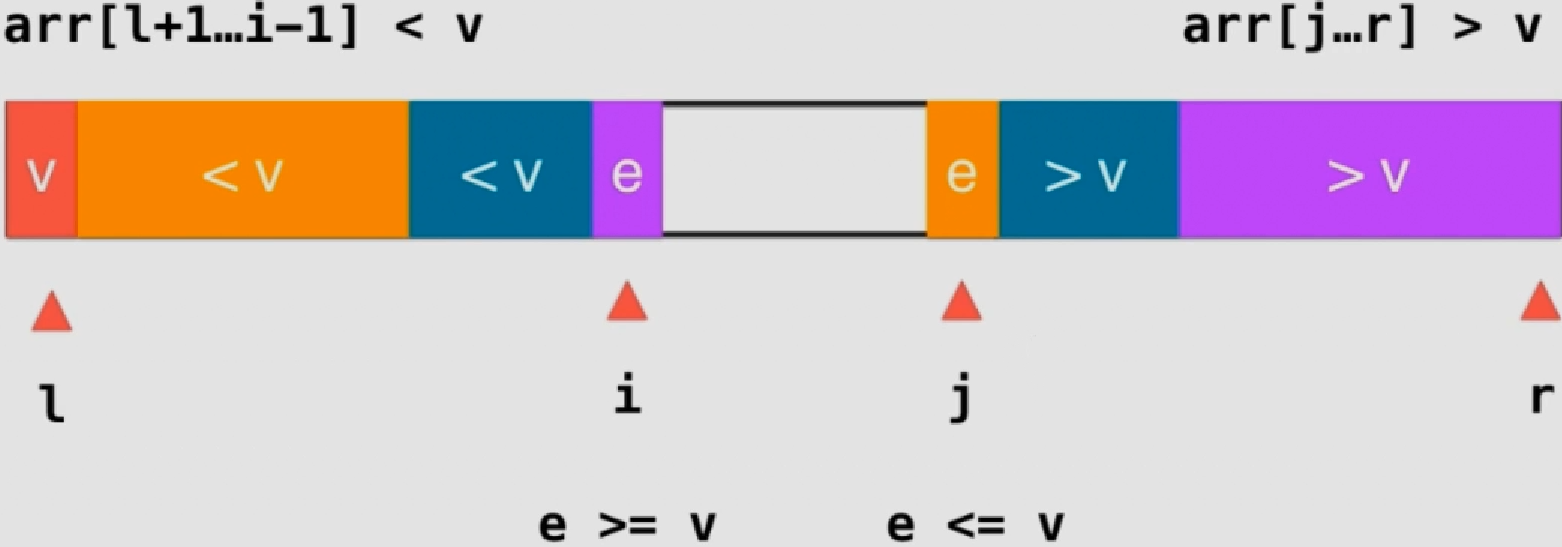
  2. 采用双路快排：两边同时进行分区操作，避免重复数据放到同一边

    双路分区操作

    • i向后扫描到e>=v时停止，j向前扫描到e<=v时停止
    • 交换i和j的元素
    • 实质上左边时<=v，右边是>=v
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    // 双路快速排序的partition
    // 返回p, 使得arr[l...p-1] <= arr[p] ; arr[p+1...r] >= arr[p]
    // 双路快排处理的元素正好等于arr[p]的时候要注意，详见下面的注释：）
    template <typename T>
    int _partition(T arr[], int l, int r){
        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap( arr[l] , arr[rand()%(r-l+1)+l] );
        T v = arr[l];

        // 使得arr[l+1...i) <= v; arr(j...r] >= v
        int i = l+1, j = r;
        while( true ){
            // 注意这里不能是arr[i] <= v
            // 否则=v的元素会全到左边
            while( i <= r && arr[i] < v )// i<=r防止越界
                i ++;

            // 注意这里不能是arr[j] >= v
            while( j >= l+1 && arr[j] > v )// i>=l+1防止越界
                j --;

            if( i > j )
                break;

            swap( arr[i] , arr[j] );
            i ++;
            j --;
        }

        swap( arr[l] , arr[j]);// 此时j一定<=v，而不能用i。i处可能会>v

        return j;// j处就是v
    }

三路快排

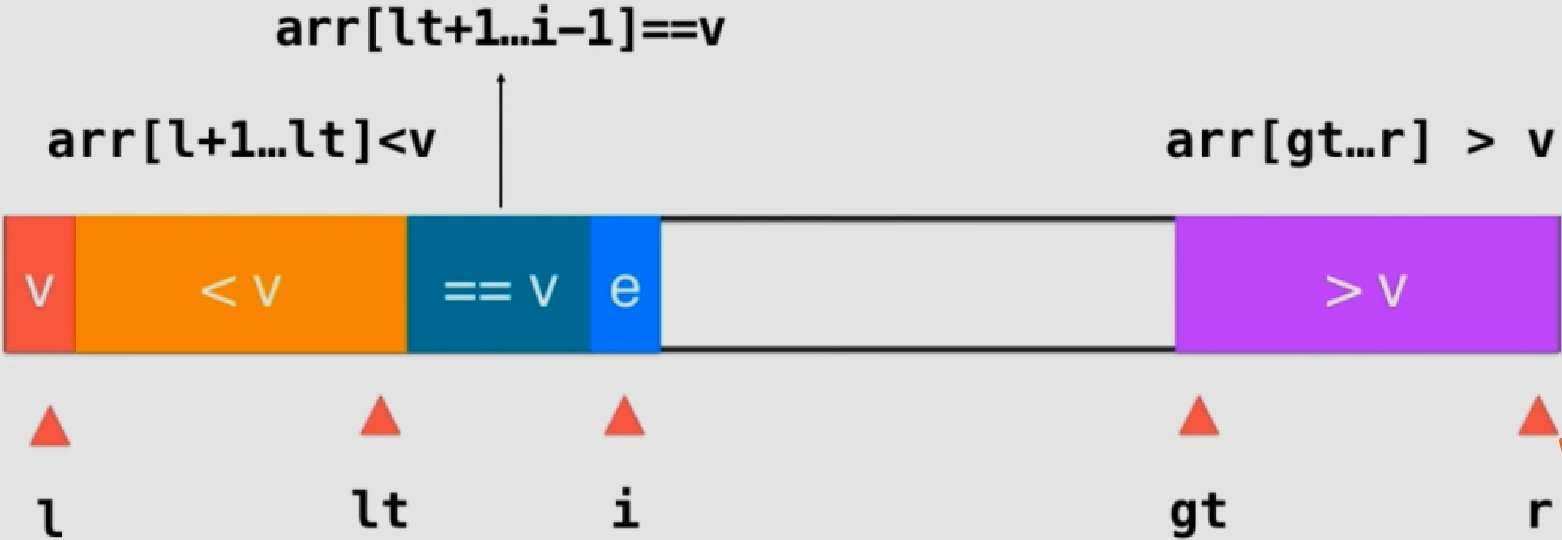
在上述双路快排的基础上，将==v的区域单独划分出来 ，形成3部分：

三路快排

  • 当e==v时，i++
  • e<v时，swap(arr[lt+1], arr[i])，lt++，i++
  • e>v时，swap(arr[gt-1], arr[i])，gt–，i由于此时交换的是新元素，所以不用改变
  • 结束时，i应该和gt重合，指向>v的第一个原始
  • 最后交换l和lt即可：swap(arr[l], arr[lt])，注意此时lt指向的是==v的第一个元素，而非<v的最后一个元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 递归的三路快速排序算法
template <typename T>
void __quickSort3Ways(T arr[], int l, int r){
    // 对于小规模数组, 使用插入排序进行优化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;// 递归的退出条件
    }

    // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
    swap( arr[l], arr[rand()%(r-l+1)+l ] );

    T v = arr[l];

    int lt = l;     // arr[l+1...lt] < v
    int gt = r + 1; // arr[gt...r] > v
    int i = l+1;    // arr[lt+1...i) == v
    while( i < gt ){
        if( arr[i] < v ){
            swap( arr[i], arr[lt+1]);
            i ++;
            lt ++;
        }
        else if( arr[i] > v ){
            swap( arr[i], arr[gt-1]);
            gt --;
        }
        else{ // arr[i] == v
            i ++;
        }
    }

    swap( arr[l] , arr[lt] );

    __quickSort3Ways(arr, l, lt-1);//注意：上一步交换后 这里需要-1
    __quickSort3Ways(arr, gt, r);
}

template <typename T>
void quickSort3Ways(T arr[], int n){

    srand(time(NULL));
    __quickSort3Ways( arr, 0, n-1);
}

215. 数组中的第K个最大元素：在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

1
2
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

1
2
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明:

  • 你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        // sort(nums.begin(), nums.end(), greater<int>());
        // return nums[k-1];

        int l = 0;
        int r = nums.size()-1;

        srand(time(NULL));
        _partition(nums, 0, nums.size()-1);
        return nums[r-k+1];
    }

    //[left, right]
    void _partition(vector<int>& nums, int left, int right)
    {
        if(left >= right) return ;
        swap(nums[left], nums[rand()%(right-left+1)+left]);
        int v = nums[left];

        int le = left;//(left, le] < v
        int gt = right+1;//[gt, right] > v
        int i = le+1;//(le, i) == v
        
        for(i; i < gt; i++)
        {
            if(nums[i] < v)
            {
                le++;
                swap(nums[le], nums[i]);
            }else if(nums[i] > v)
            {
                gt--;
                swap(nums[gt], nums[i]);
                i--;//i此时不应该变化
            }
        }
        swap(nums[left], nums[le]);

        _partition(nums, left, le-1);
        _partition(nums, gt, right);
    }
};

3.分治算法

上述问题都是分治算法的典型例子（将原问题分割成同等结构的子问题，之后将子问题逐一解决后，原问题也就得到了解决）

  • 归并排序：关键在将子问题合并上
  • 快速排序：关键在将原问题分解上

这里会直接谈论从归并排序和快速排序上引申而来的一些问题

逆序对

对这样的一个数组：8 6 2 3 1 5 7 4 ，可以从中抽出一对数组2 3，此时2<3且2在前边，这样的叫做顺序对；相应的数组2 1称为逆序对。一个数组中逆序对的数量是衡量一个数组的有序程度。当一个数组顺序排列时逆序对位0，反之逆序排列时逆序对达到了最大

  • 暴力破解法：通过双重循环考察每个数据对。时间复杂度O(n2)O(n^2)
  • 归并算法：在每次归并的比较过程中，前后两队其实是已经排好序的（假设从小到大），此时只要前一对中的元素i<后一对的元素j，即可推断出i与j及其之后的所有元素均构成逆序对。时间复杂度O(n2)O(n^2)

取出数组中第n大的元素

  • 快速排序然后定位：时间复杂度O(n2)O(n^2)
  • 在快速排序过程中，将标定点挪到合适的位置上时，该位置即为排好序后最终所处的位置，此时只要继续排序给出位置n所在的剩下那对即可。时间复杂度O(n)O(n)

三、堆和堆排序

  • 普通队列：先进先出；后进后出
  • 优先队列：出队顺序和入队顺序无关；和优先级相关

优先队列的实现方式：

入队 出队
普通数组 O(1) O(n)
顺序数组 O(n) O(1)
堆 O(lgn) O(lgn)

堆排序不占用额外的空间

1.最大堆

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

  1. 最大堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
  2. 最小堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

满二叉树：一棵深度为k且有2k−12^k-1个结点的二叉树

完全的二叉树：如果对满二叉树的结点进行编号，约定编号从根结点起，自上而下，自左而右。则深度为k的，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时，称之为完全二叉树

通俗点说就是：

完全二叉树：除了最后一层，所有层的节点数达到最大，与此同时，最后一层的所有节点都在最左侧。

满二叉树：所有层的节点数达到最大。

平衡二叉树：每一个节点的左右子树的高度差不超过1

二分搜索树：每个节点的键值大于左孩子；每个节点的键值小于右孩子；且以左右孩子为根的子树仍为二分搜索树

实现：

最大堆

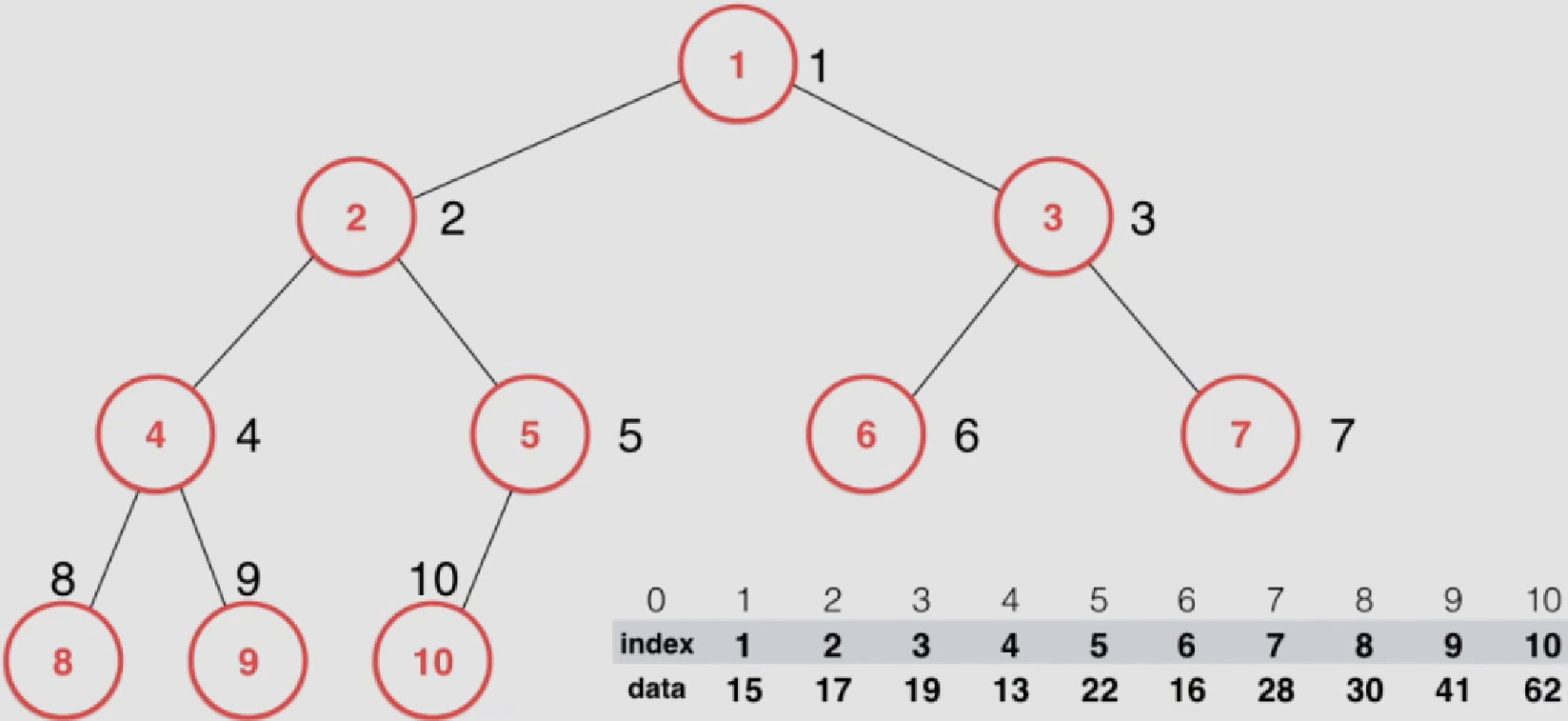
  • 根节点从1开始标记
  • 父节点标号：parent(i) = i/2，计算机中需要取整
  • 左子节点标号：left child(i) =2*i
  • 右子节点标号：right child(i) = 2*i +1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
template<typename Item>
class MaxHeap{
private:
    Item *data;//保存的数组
    int count;//当前的容量

public:
    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    MaxHeap(int capacity){
        data = new Item[capacity+1];
        count = 0;
    }

    ~MaxHeap(){
        delete[] data;
    }

    // 返回堆中的元素个数
    int size(){
        return count;
    }

    // 返回一个布尔值, 表示堆中是否为空
    bool isEmpty(){
        return count == 0;
    }
};

2.添加元素

插入

  • 将新元素放到数组最后（放到最大堆的最后），此时不是最大堆，需要调整
  • 比较新加入的节点与其父节点，如果父节点<新节点，则交换位置
  • 反复执行上一步，直至不能交换

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
template<typename Item>
class MaxHeap{
private:
    Item *data;//保存的数组
    int count;//当前的容量
    int capacity;//最大能够容纳的数量

    void shiftUp(int k){//插入 尝试将k处元素向上移动
        while( k > 1 && data[k/2] < data[k] ){
            swap( data[k/2], data[k] );
            k /= 2;
        }
    }

public:
    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    MaxHeap(int capacity){
        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }
    
    ...
    
    // 像最大堆中插入一个新的元素 item
    void insert(Item item){
        assert( count + 1 <= capacity );
        data[count+1] = item;
        count ++;
        shiftUp(count);
    }
};
  • 优化：类似于插入排序，可以通过将待排序的值存到一个副本中，计算出待插入的位置后最终再交换位置来减小swap的使用次数

3.取出元素

取出根节点元素

  • 取出根节点元素，此时需要重新排列整个树位最大堆
    • 根节点是优先级最高的节点

重新生成最大堆

  • 将最后一个元素放到取出元素的位置上
  • 比较该元素与子节点的大小，找到子节点中的最大值，如果该值>子节点，则互换
    • 注意，完全二叉树如果有子节点则一定存在左子节点
  • 重复上述步骤直至不能互换

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
template<typename Item>
class MaxHeap{
private:
    Item *data;
    int count;//当前的容量
    int capacity;//最大能够容纳的数量

    void shiftDown(int k){//取出元素 尝试将k处元素向下移动
        while( 2*k <= count ){// 存在左子节点
            int j = 2*k; // 在此轮循环中,data[k]和data[j]交换位置
            if( j+1 <= count && data[j+1] > data[j] )// 存在右子节点且右子节点较大
                j ++;
            // data[j] 是 data[2*k]和data[2*k+1]中的最大值

            if( data[k] >= data[j] ) break;
            swap( data[k] , data[j] );
            k = j;
        }
    }

public:
    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    MaxHeap(int capacity){
        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }
    
    ...

    // 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
    Item extractMax(){
        assert( count > 0 );
        Item ret = data[1];

        swap( data[1] , data[count] );
        count --;
        shiftDown(1);

        return ret;
    }

    // 获取最大堆中的堆顶元素
    Item getMax(){
        assert( count > 0 );
        return data[1];
    }
};
  • 优化：类似于插入排序，可以通过将待排序的值存到一个副本中，计算出待插入的位置后最终再交换位置来减小swap的使用次数

4.基础堆排序和Heapify

基础堆排序

基于上述最大堆的数据结构，可以构建一个排序算法（直接通过添加、取出元素排序）：

MaxHeap class：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
template<typename Item>
class MaxHeap{
private:
    Item *data;
    int count;
    int capacity;

    void shiftUp(int k){
        while( k > 1 && data[k/2] < data[k] ){
            swap( data[k/2], data[k] );
            k /= 2;
        }
    }

    void shiftDown(int k){
        while( 2*k <= count ){
            int j = 2*k;
            if( j+1 <= count && data[j+1] > data[j] ) j ++;
            if( data[k] >= data[j] ) break;
            swap( data[k] , data[j] );
            k = j;
        }
    }

public:

    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    MaxHeap(int capacity){
        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }

    ~MaxHeap(){
        delete[] data;
    }

    // 返回堆中的元素个数
    int size(){
        return count;
    }

    // 返回一个布尔值, 表示堆中是否为空
    bool isEmpty(){
        return count == 0;
    }

    // 像最大堆中插入一个新的元素 item
    void insert(Item item){
        assert( count + 1 <= capacity );
        data[count+1] = item;
        shiftUp(count+1);
        count ++;
    }

    // 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
    Item extractMax(){
        assert( count > 0 );
        Item ret = data[1];
        swap( data[1] , data[count] );
        count --;
        shiftDown(1);
        return ret;
    }

    // 获取最大堆中的堆顶元素
    Item getMax(){
        assert( count > 0 );
        return data[1];
    }
};

排序：

1
2
3
4
5
6
7
8
9
10
11
12
// heapSort1, 将所有的元素依次添加到堆中, 在将所有元素从堆中依次取出来, 即完成了排序
// 无论是创建堆的过程, 还是从堆中依次取出元素的过程, 时间复杂度均为O(nlogn)
// 整个堆排序的整体时间复杂度为O(nlogn)
template<typename T>
void heapSort1(T arr[], int n){
    MaxHeap<T> maxheap = MaxHeap<T>(n);
    for( int i = 0 ; i < n ; i ++ )
        maxheap.insert(arr[i]);

    for( int i = n-1 ; i >= 0 ; i-- )
        arr[i] = maxheap.extractMax();
}
  • 将n个元素逐个插入到一个空堆中，该过程时间复杂度为O(N∗logN)O(N*logN)

Heapify

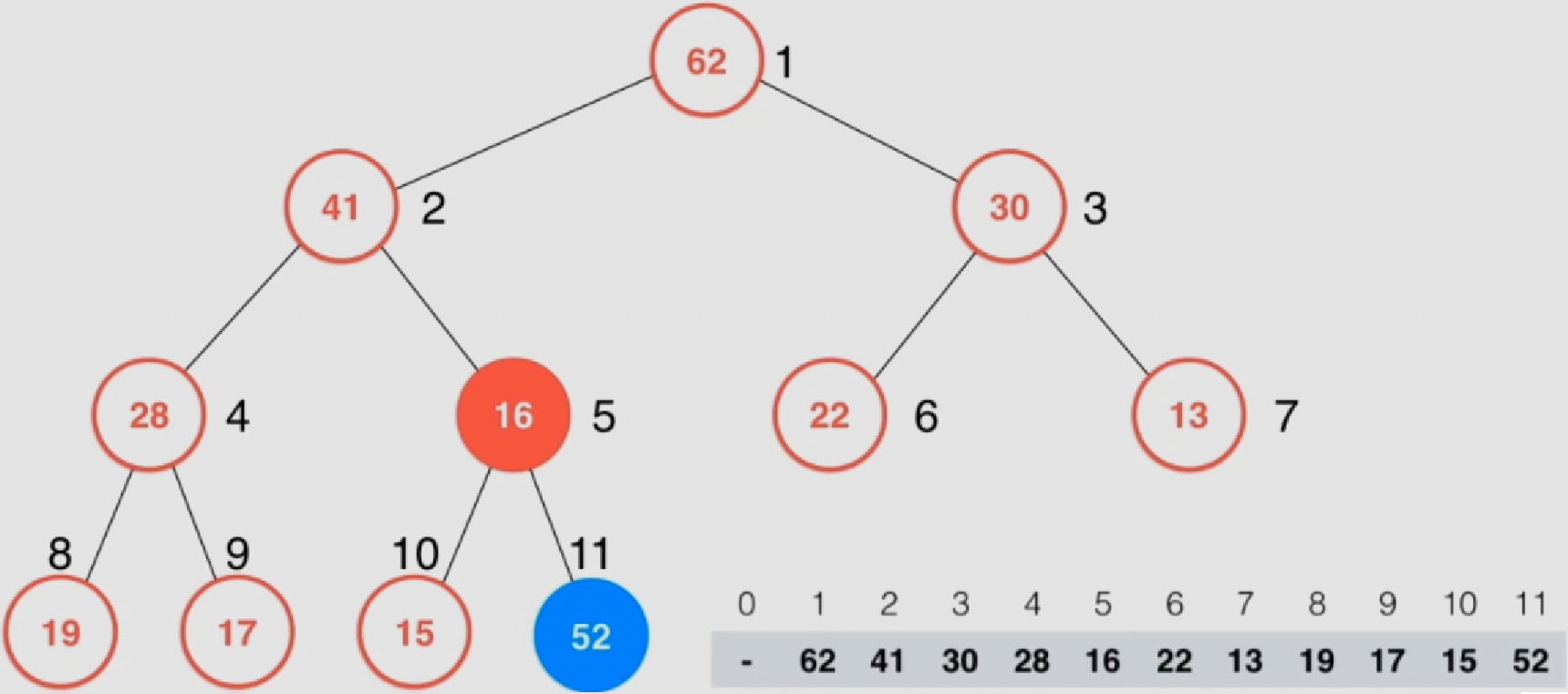
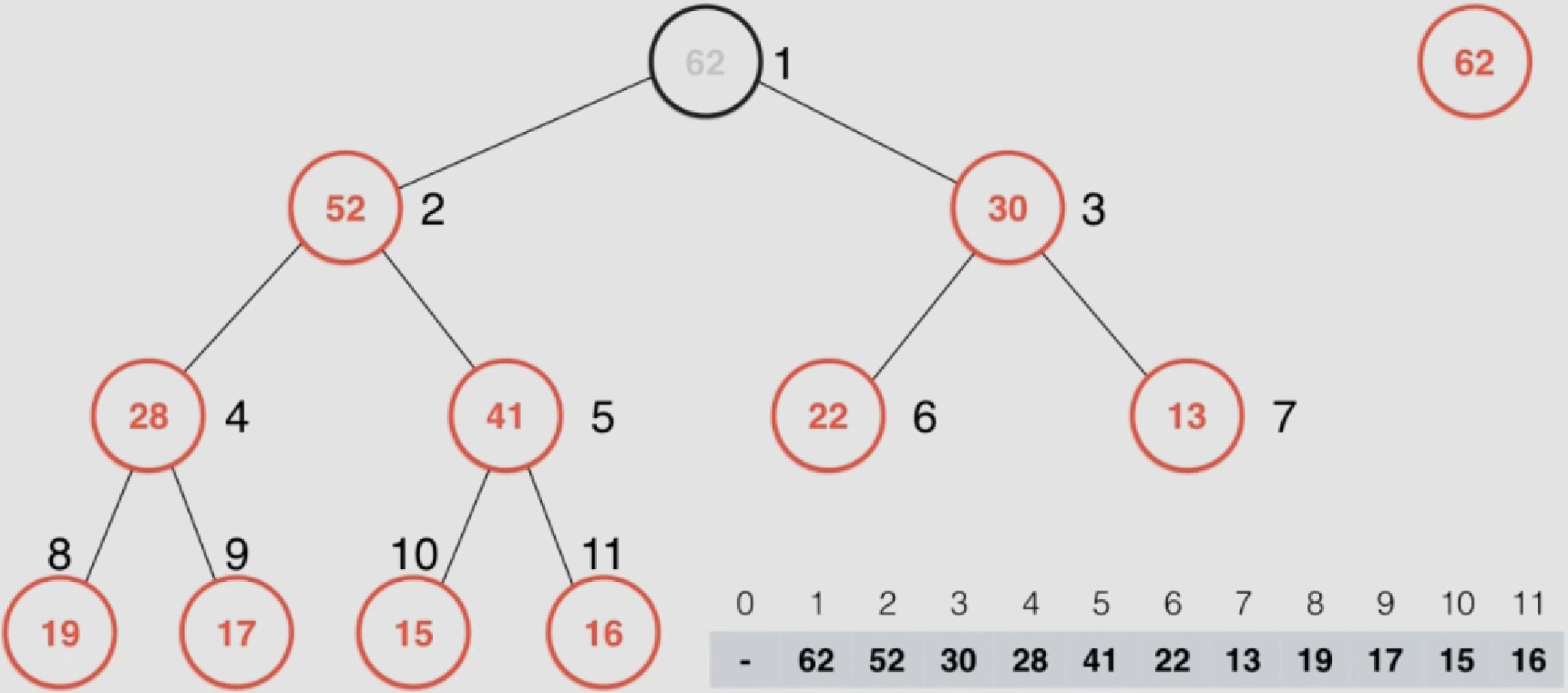
Heapify操作：给定一个数组，将这个数组中的元素按照堆的方式进行排列，该过程称为Heapify

Heapify

  • 所有的叶子节点（蓝色）均为最大堆
  • 在一棵完全二叉树来说，第一个非叶子节点的索引为所有元素个数/2
  • 从后向前（编号）检查每个不是最大堆中的节点，执行shiftDown操作即可（和子节点进行比较）
  • 整个过程后该数组就会成为一个最大堆

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
template<typename Item>
class MaxHeap{
private:
    Item *data;
    int count;
    int capacity;

    void shiftUp(int k){
        while( k > 1 && data[k/2] < data[k] ){
            swap( data[k/2], data[k] );
            k /= 2;
        }
    }

    void shiftDown(int k){
        while( 2*k <= count ){
            int j = 2*k;
            if( j+1 <= count && data[j+1] > data[j] ) j ++;
            if( data[k] >= data[j] ) break;
            swap( data[k] , data[j] );
            k = j;
        }
    }

public:

    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    MaxHeap(int capacity){
        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }

    // 构造函数, 通过一个给定数组创建一个最大堆
    // 该构造堆的过程, 时间复杂度为O(n)
    MaxHeap(Item arr[], int n){
        data = new Item[n+1];
        capacity = n;

        for( int i = 0 ; i < n ; i ++ )
            data[i+1] = arr[i];
        count = n;

        for( int i = count/2 ; i >= 1 ; i -- )// i从第一个非叶子节点开始
            shiftDown(i);
    }
    
    ...
};

算法：

1
2
3
4
5
6
7
8
9
// heapSort2, 借助我们的heapify过程创建堆
// 此时, 创建堆的过程时间复杂度为O(n), 将所有元素依次从堆中取出来, 实践复杂度为O(nlogn)
// 堆排序的总体时间复杂度依然是O(nlogn), 但是比上述heapSort1性能更优, 因为创建堆的性能更优
template<typename T>
void heapSort2(T arr[], int n){
    MaxHeap<T> maxheap = MaxHeap<T>(arr,n);
    for( int i = n-1 ; i >= 0 ; i-- )
        arr[i] = maxheap.extractMax();
}
  • Heapify直接从n/2开始，时间复杂度为O(n)O(n)，证明需要高数知识
  • 该方法快于上述基础堆排序，但是仍然慢于快速排序和归并排序
  • 更多的是用于动态数据的维护

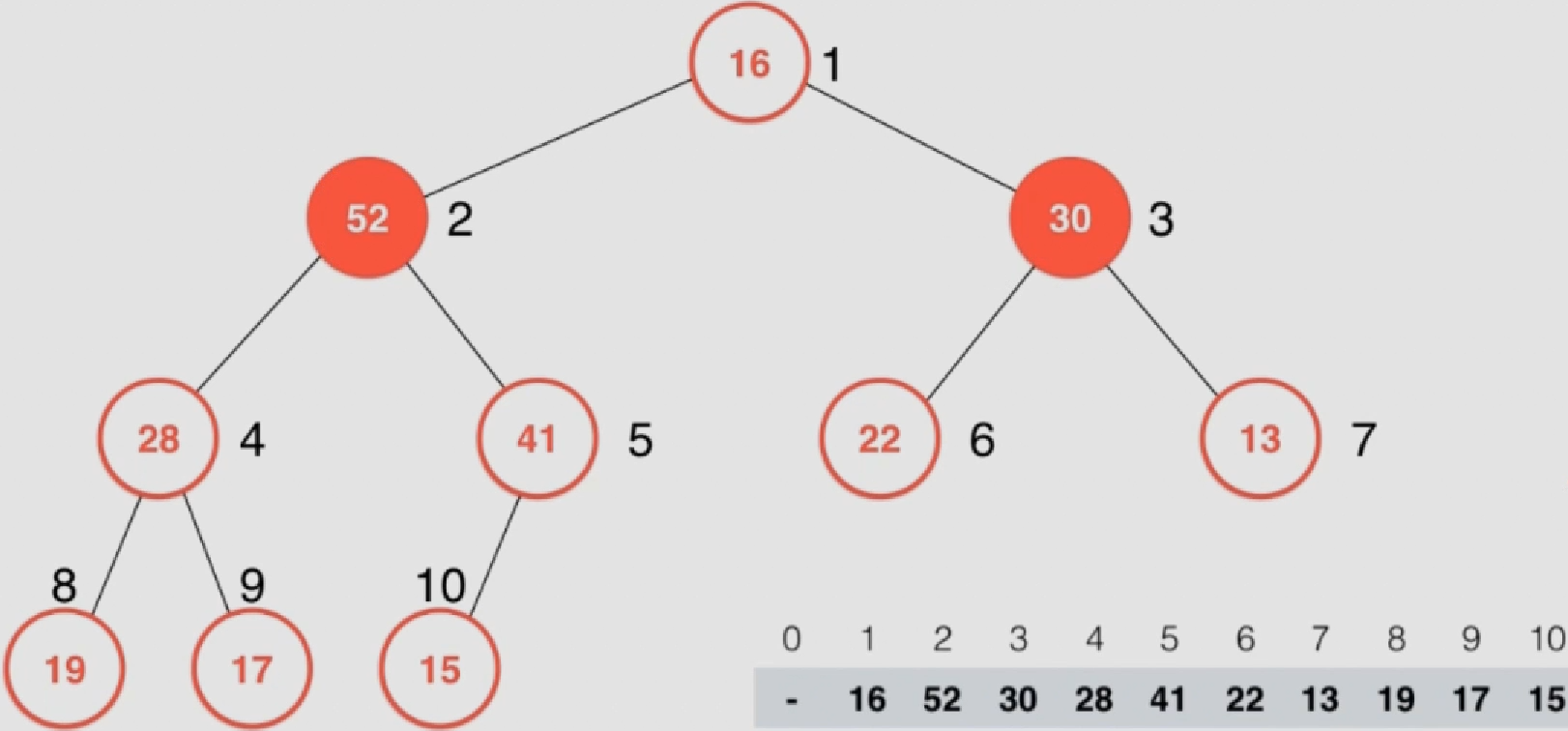
5.原地堆排序

上述Heapity过程需要重新开辟一个相同的空间，而原地堆排序不需要，空间复杂度位O(1)O(1)

原地堆排序

  • 按照Heapify方法将数组构建成一个最大堆
  • 此时第一个元素就是数组中最大元素的位置，需要将v和数组末尾元素w进行互换
  • 互换后前半部分不是最大堆，需要再次进行shiftDown操作，构建最大堆
  • 反复执行上述步骤直至排好序

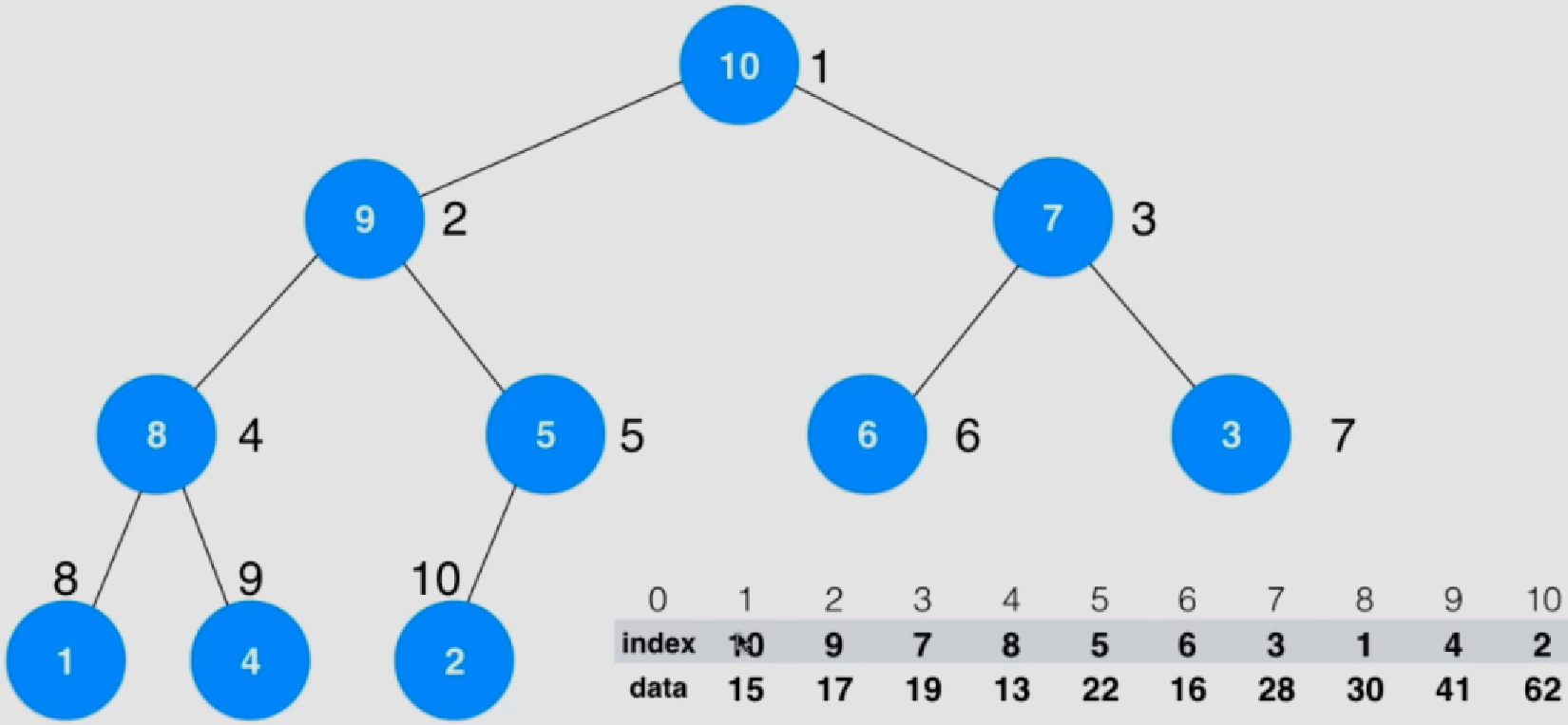
为便于数组操作，这里从0开始索引，如下规则需要改变：

  • 根节点从0开始标记（原来版本）
  • 父节点标号：parent(i) = (i-1)/2，计算机中需要取整
  • 左子节点标号：left child(i) =2*i+1
  • 右子节点标号：right child(i) = 2*i +2
  • 最后一个非叶子节点索引：(count-1)/2（原来版本）

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
// 原始的shiftDown过程
template<typename T>
void __shiftDown(T arr[], int n, int k){
    while( 2*k+1 < n ){
        int j = 2*k+1;
        if( j+1 < n && arr[j+1] > arr[j] )
            j += 1;

        if( arr[k] >= arr[j] )break;

        swap( arr[k] , arr[j] );
        k = j;
    }
}

// 优化的shiftDown过程, 使用赋值的方式取代不断的swap,
// 该优化思想和之前对插入排序进行优化的思路是一致的
template<typename T>
void __shiftDown2(T arr[], int n, int k){
    T e = arr[k];
    while( 2*k+1 < n ){
        int j = 2*k+1;
        if( j+1 < n && arr[j+1] > arr[j] )
            j += 1;

        if( e >= arr[j] ) break;

        arr[k] = arr[j];
        k = j;
    }

    arr[k] = e;
}

// 不使用一个额外的最大堆, 直接在原数组上进行原地的堆排序
template<typename T>
void heapSort(T arr[], int n){
    // 注意，此时堆是从0开始索引的
    // 从(最后一个元素的索引-1)/2开始
    // 最后一个元素的索引 = n-1
    for( int i = (n-1-1)/2 ; i >= 0 ; i -- )
        __shiftDown2(arr, n, i);

    for( int i = n-1; i > 0 ; i-- ){
        swap( arr[0] , arr[i] );
        __shiftDown2(arr, i, 0);
    }
}

6.索引堆

索引堆：将数组和索引分开存储，而真正构成堆的数据是由索引构成

索引堆也分为最大索引堆和最小索引堆，这里均采用最大索引堆

索引堆——排序前

索引堆——排序后

  • 每个圈内是索引号，圈外是二叉树节点编号（数组编号）
  • 排序后data顺序不会改变，只改变索引号index
  • 排序后，堆中元素index表示数组中的data值

相较堆排序来说：比较data值，交换index值

好处：仅仅只交换索引，不改变data。对于复杂结构的data来说效率较高

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
// 最大索引堆
template<typename Item>
class IndexMaxHeap{
private:
    Item *data;     // 最大索引堆中的数据
    int *indexes;   // 最大索引堆中的索引

    int count;
    int capacity;

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftUp( int k ){

        while( k > 1 && data[indexes[k/2]] < data[indexes[k]] ){
            swap( indexes[k/2] , indexes[k] );
            k /= 2;
        }
    }

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftDown( int k ){

        while( 2*k <= count ){
            int j = 2*k;
            if( j + 1 <= count && data[indexes[j+1]] > data[indexes[j]] )
                j += 1;

            if( data[indexes[k]] >= data[indexes[j]] )
                break;

            swap( indexes[k] , indexes[j] );
            k = j;
        }
    }

public:
    // 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
    IndexMaxHeap(int capacity){

        data = new Item[capacity+1];
        indexes = new int[capacity+1];

        count = 0;
        this->capacity = capacity;
    }

    ~IndexMaxHeap(){
        delete[] data;
        delete[] indexes;
    }

    // 返回索引堆中的元素个数
    int size(){
        return count;
    }

    // 返回一个布尔值, 表示索引堆中是否为空
    bool isEmpty(){
        return count == 0;
    }

    // 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
    // 传入的i对用户而言,是从0索引的
    void insert(int i, Item item){
        assert( count + 1 <= capacity );
        assert( i + 1 >= 1 && i + 1 <= capacity );

        i += 1;
        data[i] = item;
        indexes[count+1] = i;
        count++;

        shiftUp(count);
    }

    // 从最大索引堆中取出堆顶元素, 即索引堆中所存储的最大数据
    Item extractMax(){
        assert( count > 0 );

        Item ret = data[indexes[1]];
        swap( indexes[1] , indexes[count] );
        count--;
        shiftDown(1);
        return ret;
    }

    // 从最大索引堆中取出堆顶元素的索引
    int extractMaxIndex(){
        assert( count > 0 );

        int ret = indexes[1] - 1;
        swap( indexes[1] , indexes[count] );
        count--;
        shiftDown(1);
        return ret;
    }

    // 获取最大索引堆中的堆顶元素
    Item getMax(){
        assert( count > 0 );
        return data[indexes[1]];
    }

    // 获取最大索引堆中的堆顶元素的索引
    int getMaxIndex(){
        assert( count > 0 );
        return indexes[1]-1;
    }

    // 获取最大索引堆中索引为i的元素
    Item getItem( int i ){
        assert( i + 1 >= 1 && i + 1 <= capacity );
        return data[i+1];
    }

    // 将最大索引堆中索引为i的元素修改为newItem
    void change( int i , Item newItem ){

        i += 1;
        data[i] = newItem;

        // 找到indexes[j] = i, j表示data[i]在堆中的位置
        // 之后shiftUp(j), 再shiftDown(j)
        for( int j = 1 ; j <= count ; j ++ )
            if( indexes[j] == i ){
                shiftUp(j);
                shiftDown(j);
                return;
            }
    }

    // 测试索引堆中的索引数组index
    // 注意:这个测试在向堆中插入元素以后, 不进行extract操作有效
    bool testIndexes(){

        int *copyIndexes = new int[count+1];

        for( int i = 0 ; i <= count ; i ++ )
            copyIndexes[i] = indexes[i];

        copyIndexes[0] = 0;
        std::sort(copyIndexes, copyIndexes + count + 1);

        // 在对索引堆中的索引进行排序后, 应该正好是1...count这count个索引
        bool res = true;
        for( int i = 1 ; i <= count ; i ++ )
            if( copyIndexes[i-1] + 1 != copyIndexes[i] ){
                res = false;
                break;
            }

        delete[] copyIndexes;

        if( !res ){
            cout<<"Error!"<<endl;
            return false;
        }

        return true;
    }
};

// 使用最大索引堆进行堆排序, 来验证我们的最大索引堆的正确性
// 最大索引堆的主要作用不是用于排序, 我们在这里使用排序只是为了验证我们的最大索引堆实现的正确性
// 在后续的图论中, 无论是最小生成树算法, 还是最短路径算法, 我们都需要使用索引堆进行优化:)
template<typename T>
void heapSortUsingIndexMaxHeap(T arr[], int n){

    IndexMaxHeap<T> indexMaxHeap = IndexMaxHeap<T>(n);
    for( int i = 0 ; i < n ; i ++ )
        indexMaxHeap.insert( i , arr[i] );
    assert( indexMaxHeap.testIndexes() );

    for( int i = n-1 ; i >= 0 ; i -- )
        arr[i] = indexMaxHeap.extractMax();
}
  • 上述charge从，查找index中的元素时是通过遍历决定的，时间复杂度O(n)O(n)
  • 优化方法：再加一层rev数组

四、二分搜索树

1.二分查找法

对于有序数列（需要先排序），才能使用二分查找法，时间复杂度O(logn)O(logn)

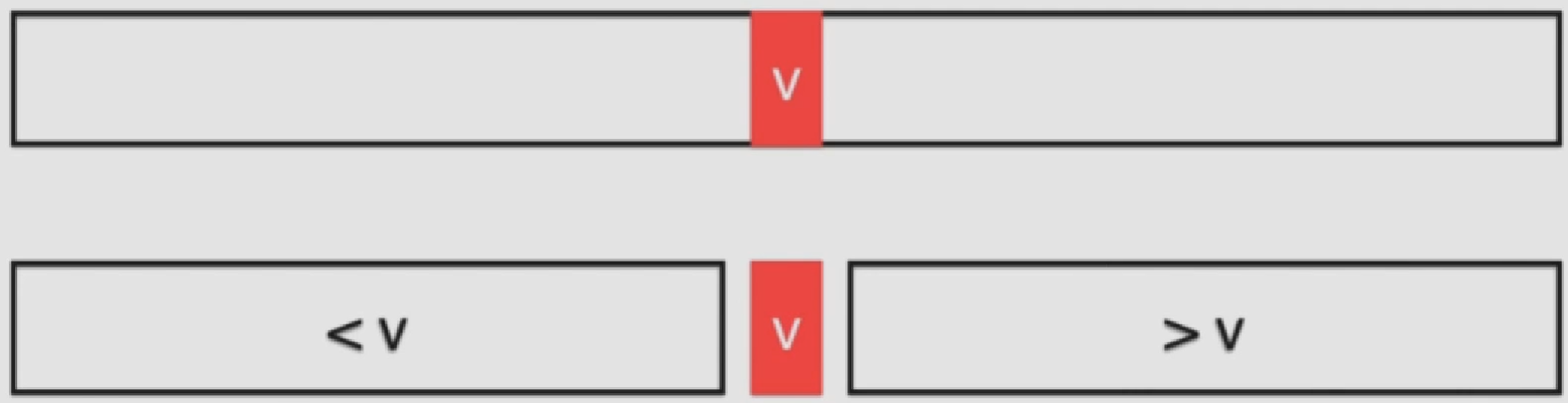
二分查找法

  • 判断中间数据v的值与待查找的值的关系：
    • v==待查找值：找到
    • 否则划分为两部分
  • 再对应区域继续重复上述部分

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// 二分查找法,在有序数组arr中,查找target
// 如果找到target,返回相应的索引index
// 如果没有找到target,返回-1
template<typename T>
int binarySearch(T arr[], int n, T target){
    // 在arr[l...r]之中查找target
    int l = 0, r = n-1;
    while( l <= r ){
        //int mid = (l + r)/2;
        // 防止极端情况下的整形溢出，使用下面的逻辑求出mid
        int mid = l + (r-l)/2;

        if( arr[mid] == target )
            return mid;

        if( arr[mid] > target )
            r = mid - 1;
        else
            l = mid + 1;
    }
    return -1;
}


// 用递归的方式写二分查找法
template<typename T>
int __binarySearch2(T arr[], int l, int r, T target){
    if( l > r )
        return -1;

    //int mid = (l+r)/2;
    // 防止极端情况下的整形溢出，使用下面的逻辑求出mid
    int mid = l + (r-l)/2;

    if( arr[mid] == target )
        return mid;
    else if( arr[mid] > target )
        return __binarySearch2(arr, l, mid-1, target);
    else
        return __binarySearch2(arr, mid+1, r, target);
}
  • 递归实现通常较容易实现
  • 递归在性能上非略差

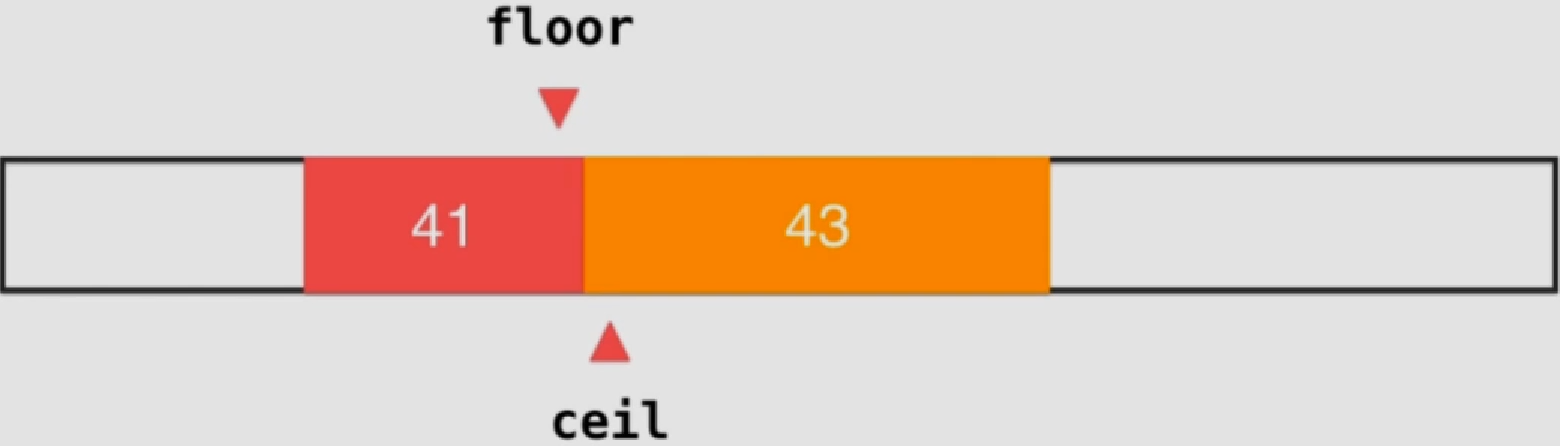
floor和ceil

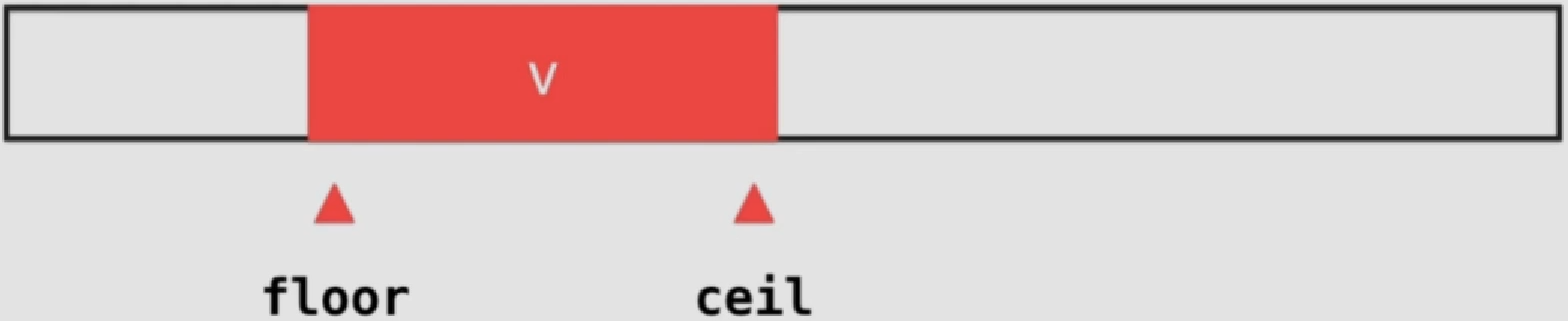
查找的元素中如果有重复元素的话，上述二分查找法不能保证找到的索引是该重复元素中需要的索引

floor和ceil

  • floor为待查找元素出现的第一个位置

  • ceil为最后一个

  • 对于不存在的情况，返回结果比二分查找更好

    待查找元素42不存在

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
// 二分查找法, 在有序数组arr中, 查找target
// 如果找到target, 返回第一个target相应的索引index
// 如果没有找到target, 返回比target小的最大值相应的索引, 如果这个最大值有多个, 返回最大索引
// 如果这个target比整个数组的最小元素值还要小, 则不存在这个target的floor值, 返回-1
template<typename T>
int floor(T arr[], int n, T target){
    assert( n >= 0 );
    // 寻找比target小的最大索引
    int l = -1, r = n-1;
    while( l < r ){
        // 使用向上取整避免死循环
        int mid = l + (r-l+1)/2;
        if( arr[mid] >= target )// 通过这里来找到target-1的位置
            r = mid - 1;
        else
            l = mid;
    }

    assert( l == r );

    // 如果该索引+1就是target本身, 该索引+1即为返回值
    if( l + 1 < n && arr[l+1] == target )
        return l + 1;

    // 否则, 该索引即为返回值
    return l;
}


// 二分查找法, 在有序数组arr中, 查找target
// 如果找到target, 返回最后一个target相应的索引index
// 如果没有找到target, 返回比target大的最小值相应的索引, 如果这个最小值有多个, 返回最小的索引
// 如果这个target比整个数组的最大元素值还要大, 则不存在这个target的ceil值, 返回整个数组元素个数n
template<typename T>
int ceil(T arr[], int n, T target){
    assert( n >= 0 );
    // 寻找比target大的最小索引值
    int l = 0, r = n;
    while( l < r ){
        // 使用普通的向下取整即可避免死循环
        int mid = l + (r-l)/2;
        if( arr[mid] <= target )// 通过这里来找到target+1的位置
            l = mid + 1;
        else // arr[mid] > target
            r = mid;
    }

    assert( l == r );

    // 如果该索引-1就是target本身, 该索引+1即为返回值
    if( r - 1 >= 0 && arr[r-1] == target )
        return r-1;

    // 否则, 该索引即为返回值
    return r;
}

2.二分搜索树

优势：

时间复杂度 查找元素 插入元素 删除元素
普通数组 O(n) O(n) O(n)
顺序数组 O(logn) O(n) O(n)
二分搜索树 O(logn) O(logn) O(logn)

一般用于查找表/字典这种键值对的实现

需要满足：

二分搜索树

  • 是一颗二叉树
  • 每个节点的键值大于左孩子（及其全部子节点），小于右孩子（及其全部子节点）
  • 以左右孩子为根的子树仍为二分搜索树
  • 圈中内容为键
  • 不像最大堆一样，二分搜索树不一定为完全二叉树，所以一般不用数组表示，而通过采用指针连接的node节点

基本结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// 二分搜索树
template <typename Key, typename Value>
class BST{

private:
    // 树中的节点为私有的结构体, 外界不需要了解二分搜索树节点的具体实现
    struct Node{
        Key key;
        Value value;
        Node *left;
        Node *right;

        Node(Key key, Value value){
            this->key = key;
            this->value = value;
            this->left = this->right = NULL;
        }

        Node(Node *node){
            this->key = node->key;
            this->value = node->value;
            this->left = node->left;
            this->right = node->right;
        }
    };

    Node *root; // 根节点
    int count;  // 树中的节点个数

public:
    // 构造函数, 默认构造一棵空二分搜索树
    BST(){
        root = NULL;
        count = 0;
    }

    // 析构函数, 释放二分搜索树的所有空间
    ~BST(){
        destroy( root );// 这里用到了后序遍历，详见后文 遍历 章节
    }

    // 返回二分搜索树的节点个数
    int size(){
        return count;
    }

    // 返回二分搜索树是否为空
    bool isEmpty(){
        return count == 0;
    }
    
    ...
}

插入

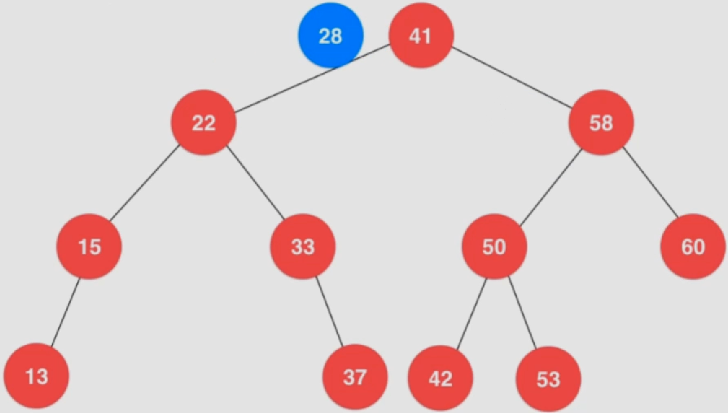
插入元素——28

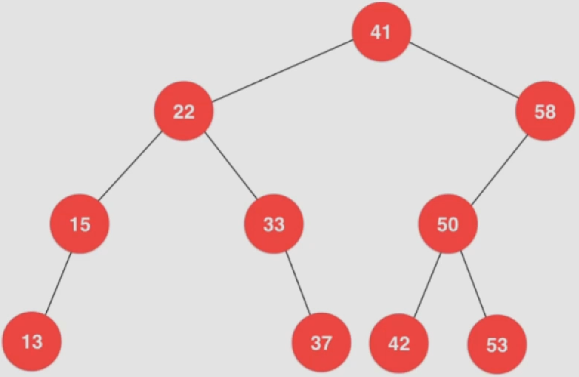
  • 将待插入元素和根节点（41）进行比较，发现小于根节点
  • 与左子节点（22）进行比较，发现大于该节点
  • 与右子节点（33）进行比较，发现小于该节点
  • 此时该位置为空，故最终成为33这个节点的左子节点

注意：当待插入节点在二分搜索树中已经存在时，通常来说会覆盖掉之前的节点的值（键相同，覆盖值）

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
// 返回插入新节点后的二分搜索树的根
Node* insert(Node *node, Key key, Value value){
    if( node == NULL ){//递归终止条件1
        count ++;
        return new Node(key, value);
    }

    if( key == node->key ) // 已经存在，直接覆盖
        node->value = value;//递归终止条件2
    else if( key < node->key )
        node->left = insert( node->left , key, value);
    else    // key > node->key
        node->right = insert( node->right, key, value);

    return node;
}

查找

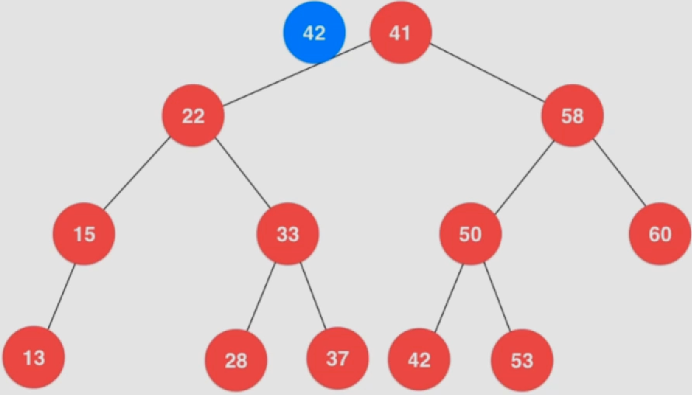
查找元素——42

  • 将待查找元素和根节点（41）进行比较，发现大于根节点
  • 与右子节点（58）进行比较，发现小于该节点
  • 与左子节点（50）进行比较，发现小于该节点
  • 最终查找50的左子节点，发现刚好相等，查找成功

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
bool contain(Node* node, Key key){
    if( node == NULL ) // 递归结束条件
        return false;

    if( key == node->key ) // 成功找到
        return true;
    else if( key < node->key )
        return contain( node->left , key );
    else // key > node->key
        return contain( node->right , key );
}

// 在以node为根的二分搜索树中查找key所对应的value, 递归算法
// 若value不存在, 则返回NULL
Value* search(Node* node, Key key){
    if( node == NULL ) // 递归结束条件
        return NULL;

    if( key == node->key ) // 成功找到
        return &(node->value);
    else if( key < node->key )
        return search( node->left , key );
    else // key > node->key
        return search( node->right, key );
}

遍历（深度优先）

深度优先遍历，DFS（Depth First Search）：直接扫描到整个树的最深层，再依次回溯，来遍历整棵树。时间复杂度O(n)O(n)。根据执行动作的时间不同分为以下几种方式：

  1. 前序遍历：先访问当前节点，再依次递归访问左右子树
  2. 中序遍历：先递归访问左子树，再访问自身，再递归访问右子树
    • 对于二分搜索树来说，中序遍历会将元素从小到大排序输出
  3. 后续遍历：先递归访问左右子树，再访问自身节点
    • 最典型的应用：释放二叉树

注意：上述中的访问，可以理解为执行该节点对应的动作，如输出自身的值

一个便于理解的方法：

一种理解方法

  • 每次遍历时（自身->左子树->自身->右子树->自身，共三次），一个节点都会扫描过三次，对应上图中的三个点
  • 前序遍历是在第一次扫描时（对应第一个点），就执行对应的动作
  • 中序遍历是在第二次扫描时（对应第二个点），就执行对应的动作
  • 后序遍历是在第三次扫描时（对应最后一个点），就执行对应的动作

前序遍历：

1
2
3
4
5
6
7
8
// 对以node为根的二叉搜索树进行前序遍历, 递归算法
void preOrder(Node* node){
    if( node != NULL ){
        cout<<node->key<<endl;
        preOrder(node->left);
        preOrder(node->right);
    }
}

中序遍历：

1
2
3
4
5
6
7
8
// 对以node为根的二叉搜索树进行中序遍历, 递归算法
void inOrder(Node* node){
    if( node != NULL ){
        inOrder(node->left);
        cout<<node->key<<endl;
        inOrder(node->right);
    }
}

后序遍历：

1
2
3
4
5
6
7
8
// 对以node为根的二叉搜索树进行后序遍历, 递归算法
void postOrder(Node* node){
    if( node != NULL ){
        postOrder(node->left);
        postOrder(node->right);
        cout<<node->key<<endl;
    }
}

上述析构函数就是利用到了后序遍历：

1
2
3
4
5
6
7
8
9
10
11
// 释放以node为根的二分搜索树的所有节点
// 采用后续遍历的递归算法
void destroy(Node* node){
    if( node != NULL ){
        destroy( node->left );
        destroy( node->right );

        delete node;
        count --;
    }
}

遍历（广度优先）

广度优先遍历，BFS（Breadth First Search）：从根节点开始，对每层的所有节点依次进行扫描。时间复杂度O(n)O(n)。

通常来说广度优先遍历需要借助FIFO队列来实现：

  1. 将根节点入队
  2. 当队列不为空时，取出队列中的第一个元素并执行对应的动作（如打印）
  3. 将取出元素的左右子节点依次入队
  4. 重复上述2 3步骤，直到整棵树遍历结束

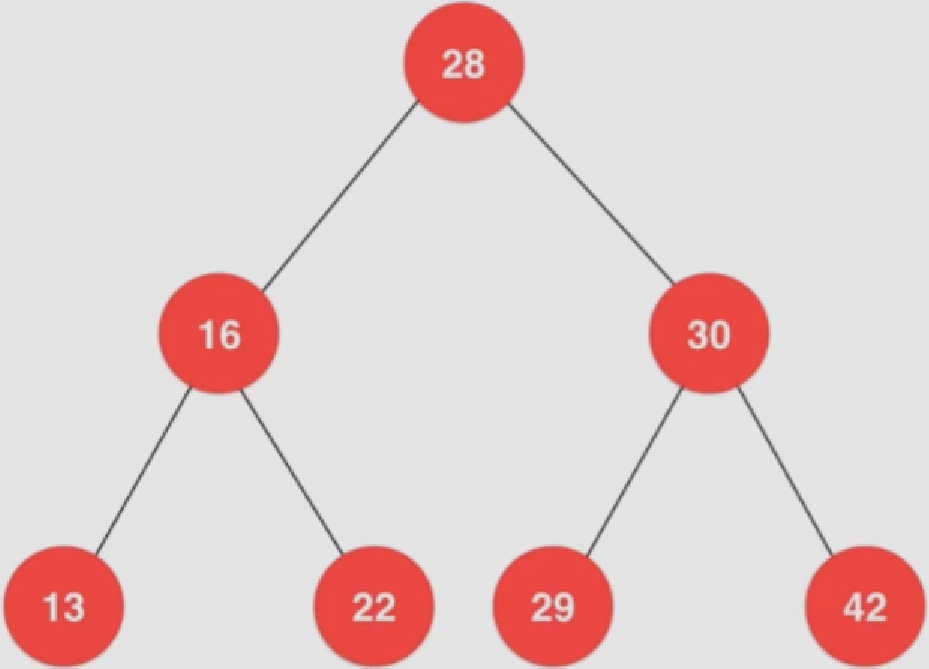
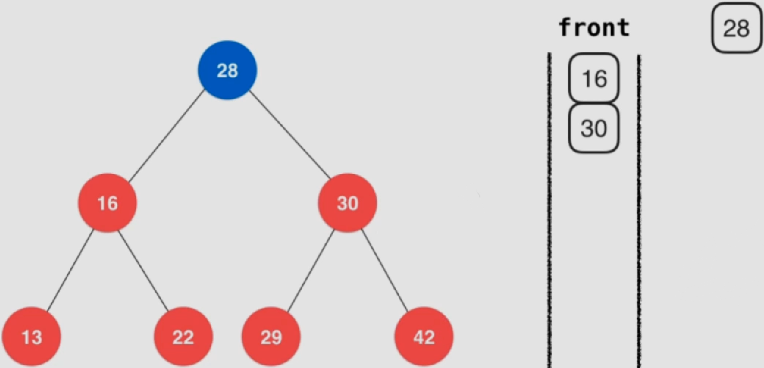
广度优先遍历

  • 取出根节点28的同时，将左右子节点16、30分别入队

实现：

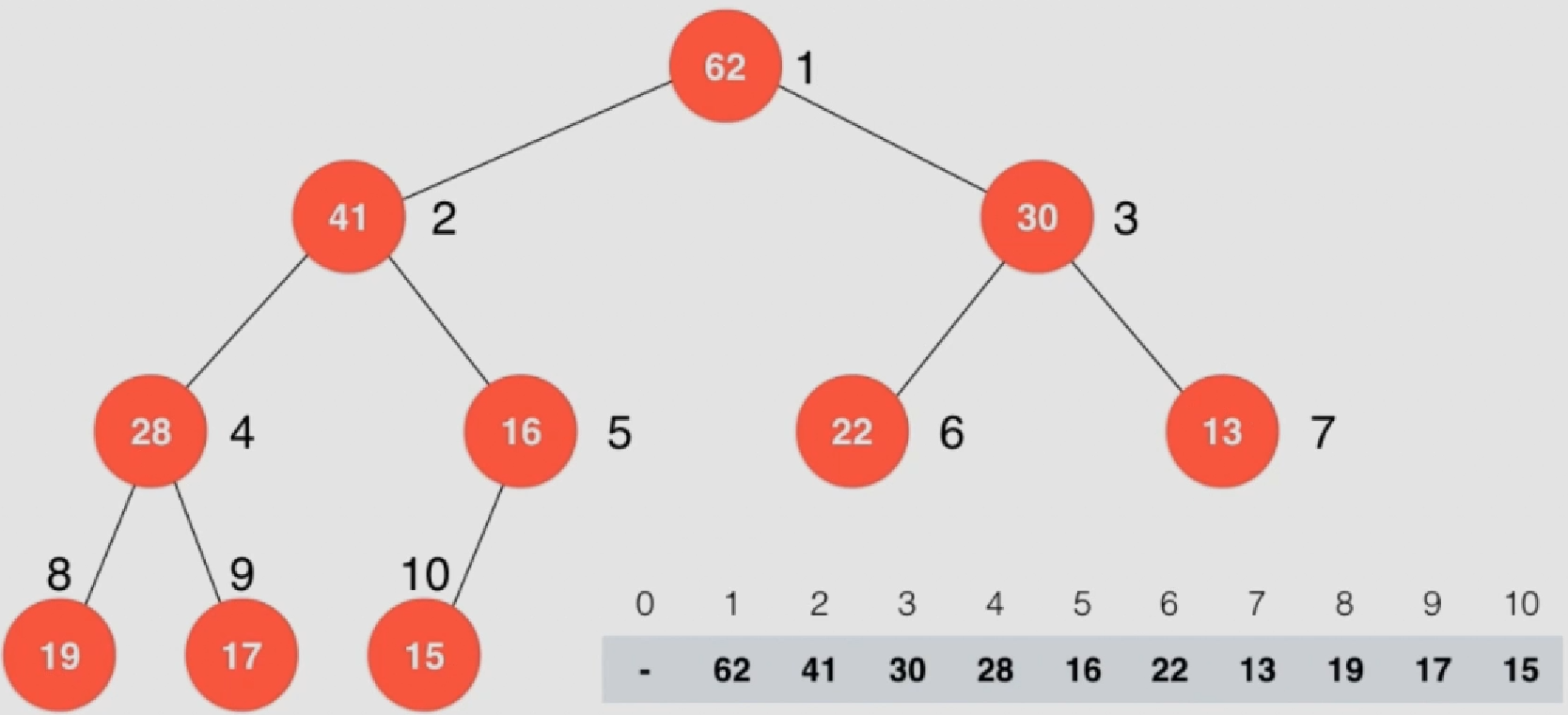
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 二分搜索树的层序遍历
void levelOrder() {
    if (root == NULL) return;

    queue<Node *> q;//使用c++自带的队列queue
    q.push(root);
    while (!q.empty()) {
        Node *node = q.front();//取出队首元素
        q.pop();//出队

        cout << node->key << endl;//执行队首元素对应的动作
        //将node的左右子节点分别入队
        if (node->left)
            q.push(node->left);
        if (node->right)
            q.push(node->right);
    }
}

删除

时间复杂度O(nlogn)O(nlogn)

最小最大值

在二分搜索树中：

  • 最小值：二分搜索树的最左子节点（一直找左节点，直到为空）
  • 最大值：二分搜索树的最右子节点（一直找右节点，直到为空）

删除最大值——58

  • 找到最大值——58
  • 删掉最大值后剩余部分节点直接挂载58下
  • 最小值同理

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
Node* removeMin(Node* node){
    if( node->left == NULL ){//递归终止条件：找到最小节点

        Node* rightNode = node->right;//最小节点的右节点不管存不存在都挂回到删掉的位置上
        delete node;
        count --;
        return rightNode;
    }

    node->left = removeMin(node->left);//递归查找，并挂回到删掉的位置上
    return node;
}

// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
Node* removeMax(Node* node){
    if( node->right == NULL ){

        Node* leftNode = node->left;
        delete node;
        count --;
        return leftNode;
    }

    node->right = removeMax(node->right);
    return node;
}
任意节点

通过上述可以看出：

  • 最小值所在节点只会有右子节点
  • 最大值所在节点只会有左子节点

从上述可以推断出：

  1. 对于只存在一个子节点的节点，可以直接删除掉该节点，然后将子节点挂上来
  2. 对于存在两个子节点的节点，可以通过Hubbard Deletion方法来删除

Hubbard Deletion方法：

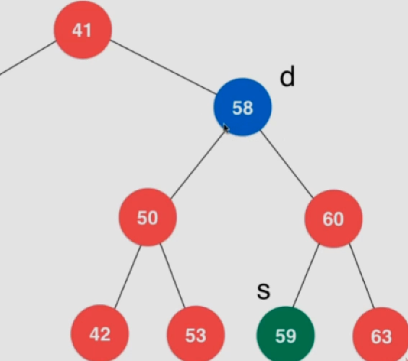
Hubbard Deletion方法

  1. 找到要删除元素d（58）的右子树中的最小值（或者左子树的最大值，称为前驱节点），此时为节点s（59），称该节点为d的后继节点
  2. 将节点s换到节点d的位置上去
    1. 删除后继节点s（59）
    2. 将该节点s的右子节点指向节点d（58）的右子树（60）
    3. 将节点s的左子节点指向节点d（58）的左子树（50）
    4. 删除节点d（58）
    5. 将新节点s（59）挂在原来节点d的位置上

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
// 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
Node* remove(Node* node, Key key){
    if( node == NULL )
        return NULL;

    if( key < node->key ){
        node->left = remove( node->left , key );
        return node;
    }
    else if( key > node->key ){
        node->right = remove( node->right, key );
        return node;
    }
    else{   // key == node->key

        // 待删除节点左子树为空的情况
        if( node->left == NULL ){
            Node *rightNode = node->right;
            delete node;
            count --;
            return rightNode;
        }

        // 待删除节点右子树为空的情况
        if( node->right == NULL ){
            Node *leftNode = node->left;
            delete node;
            count--;
            return leftNode;
        }

        // 待删除节点左右子树均不为空的情况

        // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
        // 用这个节点顶替待删除节点的位置
        Node *successor = new Node(minimum(node->right));//找到右节点中的最小节点并复制一份
        count ++;//removeMin中需要操作该变量

        successor->right = removeMin(node->right);//删除右节点中的最小节点 并返回右子树的根节点复制给后继节点successor
        successor->left = node->left;//继承node节点的左子树节点

        delete node;//删除找到的节点
        count --;

        return successor;//新的根节点
    }
}

顺序性

二分搜索树具有一定的顺序性，不仅能够定位一个元素，而且还能用于处理一些和元素顺序相关的问题，具体包括：

  1. 查询最小、最大元素（minimum、maximum）
  2. 查找前驱元素、后驱元素（predecessor、successor）
  3. 找到相应元素的floor、ceil（定义详见floor和ceil，与第2点不同的是，第3点中的元素可以不存在树中）
  4. rank、select
    • rank：xx元素排名第几
    • select：排名第几的元素是谁

floor和ceil的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// 在以node为根的二叉搜索树中, 寻找key的floor值所处的节点, 递归算法
Node* floor(Node* node, Key key){
    if( node == NULL )
        return NULL;

    // 如果node的key值和要寻找的key值相等
    // 则node本身就是key的floor节点
    if( node->key == key )
        return node;

    // 如果node的key值比要寻找的key值大
    // 则要寻找的key的floor节点一定在node的左子树中
    if( node->key > key )
        return floor( node->left , key );

    // 如果node->key < key
    // 则node有可能是key的floor节点, 也有可能不是(存在比node->key大但是小于key的其余节点)
    // 需要尝试向node的右子树寻找一下
    Node* tempNode = floor( node->right , key );
    if( tempNode != NULL )
        return tempNode;

    return node;
}

// 在以node为根的二叉搜索树中, 寻找key的ceil值所处的节点, 递归算法
Node* ceil(Node* node, Key key){
    if( node == NULL )
        return NULL;

    // 如果node的key值和要寻找的key值相等
    // 则node本身就是key的ceil节点
    if( node->key == key )
        return node;

    // 如果node的key值比要寻找的key值小
    // 则要寻找的key的ceil节点一定在node的右子树中
    if( node->key < key )
        return ceil( node->right , key );

    // 如果node->key > key
    // 则node有可能是key的ceil节点, 也有可能不是(存在比node->key小但是大于key的其余节点)
    // 需要尝试向node的左子树寻找一下
    Node* tempNode = ceil( node->left , key );
    if( tempNode != NULL )
        return tempNode;

    return node;
}

局限性

同样的数据可以对应不同的二分搜索树，所以在某些情况下可能会退化为链表，相应的操作会从O(nlongn)O(nlongn)退化为O(n)O(n)，如下所以：

局限性

解决方法：

  1. 打乱数据，使得不会出现上述极端情况
  2. 在不能打乱数据的情况下（如几乎有序的数据流等情况下），可以通过平衡二叉树——红黑树来实现
    • 平衡二叉树中还包括诸如：2-3树、AVL树、Splay树
    • 平衡二叉树和堆的结合：Treap
    • trie字典树：适合字典词频统计

树形问题

由于树这种结构的定义具有天然的递归性，所以在求解时利用递归的方法也天然的具有这种树的性质，如：

  • 归并排序
  • 快速排序

使用递归来求解的问题，最常见的就是搜索问题

五、并查集

一种很不一样的树形结构：对于一组数据，主要支持两个操作：

  1. union(p,q)：求p和q的并集，即p∪qp\cup q
  2. find§：查找元素p所在的组

并查集可以回答下述问题：

  1. isConnected(p,q)：p和q是否在一块

时间复杂度近乎是O(1)O(1)（通过优化后）

Quick Find结构

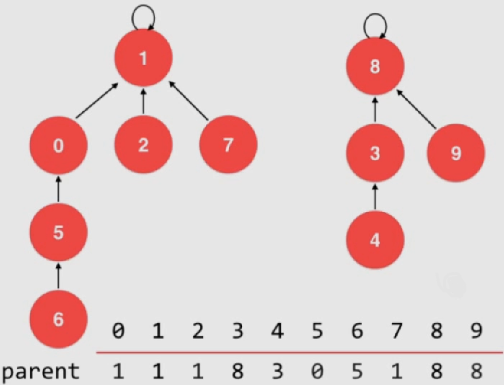
基本数据表示：

Quick Find结构

  • 数组的索引用来表示元素（横线上方元素）
  • 数组的每个元素表示对应元素所属的组（横线下方元素）

特点：

  1. 查找（find）元素所属的组特别快，时间复杂度为O(1)O(1)
  2. 并（union）操作时间复杂度为O(n)O(n)

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
namespace UF1 {
    class UnionFind {
    private:
        int *id;    // 本质就是一个数组，其中的内容是组号
        int count;  // 数据个数

    public:
        // 构造函数
        UnionFind(int n) {
            count = n;
            id = new int[n];
            // 初始化, 每一个id[i]指向自己, 没有合并的元素
            for (int i = 0; i < n; i++)
                id[i] = i;
        }

        // 析构函数
        ~UnionFind() {
            delete[] id;
        }

        // 查找过程, 查找元素p所对应的集合编号
        int find(int p) {
            assert(p >= 0 && p < count);
            return id[p];
        }

        // 查看元素p和元素q是否所属一个集合
        // O(1)复杂度
        bool isConnected(int p, int q) {
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(n) 复杂度
        void unionElements(int p, int q) {

            int pID = find(p);
            int qID = find(q);

            if (pID == qID) // 元素已经在同一个集合中
                return;

            // 合并过程需要遍历一遍所有元素, 将两个元素的所属集合编号合并
            for (int i = 0; i < count; i++)
                if (id[i] == pID)
                    id[i] = qID;
        }
    };
}

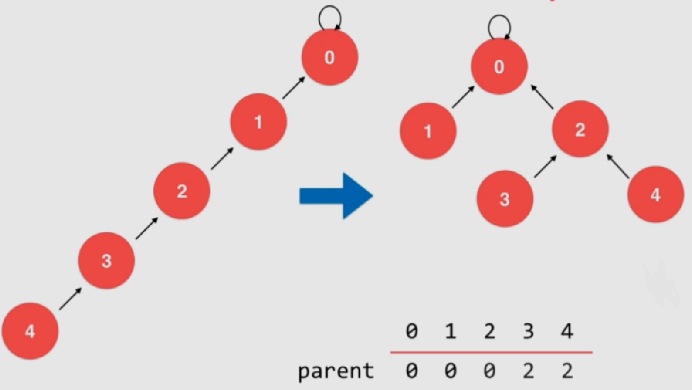
Quick Union结构

将每个元素视为一个节点，如果两个元素为同一个组，则通过指针进行连接，如下所示：

3和2在同一个组中，连接在一起

通过上述方法将所有元素进行连接。而实际上并不需要通过指针进行连接，这里可以通过一个数组parent来表示这种关系：

0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
  • 上方为parent数组的序号，下方为元素
  • parent[i]：即元素值，表示i元素所指向的父亲元素的序号
  • 初始化时每个元素都指向自己，即parent[i] = i

如下情况，该数组变为：

某种情况

  • 合并过程中，只需要将待合并的元素的根部进行连接即可
  • 查找过程和树的高度相关，在绝大多数情况下树的高度远远小于整个数据个数

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
namespace UF2{
    class UnionFind{
    private:
        // 使用一个数组构建一棵指向父节点的树
        // parent[i]表示第i个元素所指向的父节点
        int* parent;
        int count;  // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            this->count = count;
            // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
            for( int i = 0 ; i < count ; i ++ )
                parent[i] = i;
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );
            // 不断去查询自己的父亲节点, 直到到达根节点
            // 根节点的特点: parent[p] == p
            while( p != parent[p] )
                p = parent[p];
            return p;
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){
            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            parent[pRoot] = qRoot;
        }
    };
}

union优化——元素大小

上述过程没有考虑到合并过程中时元素多的一组向元素少的一组合并还是反过来，可以通过在根节点处设置一个计数器来实现一个层数更低的树

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
namespace UF3{
    class UnionFind{
    private:
        int* parent; // parent[i]表示第i个元素所指向的父节点
        int* sz;     // sz[i]表示以i为根的集合中元素个数
        int count;   // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            sz = new int[count];
            this->count = count;
            for( int i = 0 ; i < count ; i ++ ){
                parent[i] = i;
                sz[i] = 1;
            }
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
            delete[] sz;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );
            // 不断去查询自己的父亲节点, 直到到达根节点
            // 根节点的特点: parent[p] == p
            while( p != parent[p] )
                p = parent[p];
            return p;
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){
            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            // 根据两个元素所在树的元素个数不同判断合并方向
            // 将元素个数少的集合合并到元素个数多的集合上
            if( sz[pRoot] < sz[qRoot] ){
                parent[pRoot] = qRoot;//指向元素多的根
                sz[qRoot] += sz[pRoot];
            }
            else{
                parent[qRoot] = pRoot;
                sz[pRoot] += sz[qRoot];
            }
        }
    };
}

union优化——元素层数

当出现如下所示是特殊情况时：

按元素大小来处理时的特殊情况

若按照元素大小来进行优化，此时当需要将4和2进行合并时，4所在的树8会合并到2所在的树7上去，此时整棵树的层数变为了4层；如果反之将树7挂到树8下，则层数为3。

由上可知基于元素大小并不一定可靠，而需要根据元素层数来进行判断，通常而言，在并查集中元素层数称为rank：

  • rank[i]：根节点为i的树的高度

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
namespace UF4{
    class UnionFind{
    private:
        int* rank;   // rank[i]表示以i为根的集合所表示的树的层数
        int* parent; // parent[i]表示第i个元素所指向的父节点
        int count;   // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            rank = new int[count];
            this->count = count;
            for( int i = 0 ; i < count ; i ++ ){
                parent[i] = i;
                rank[i] = 1;
            }
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
            delete[] rank;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );
            // 不断去查询自己的父亲节点, 直到到达根节点
            // 根节点的特点: parent[p] == p
            while( p != parent[p] )
                p = parent[p];
            return p;
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){
            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            // 根据两个元素所在树的元素个数不同判断合并方向
            // 将元素个数少的集合合并到元素个数多的集合上
            if( rank[pRoot] < rank[qRoot] ){//注意：此时不需要修改rank
                parent[pRoot] = qRoot;
            }
            else if( rank[qRoot] < rank[pRoot]){
                parent[qRoot] = pRoot;
            }
            else{ // rank[pRoot] == rank[qRoot]
                parent[pRoot] = qRoot;
                rank[qRoot] += 1;   // 此时, 需要维护rank的值
            }
        }
    };
}

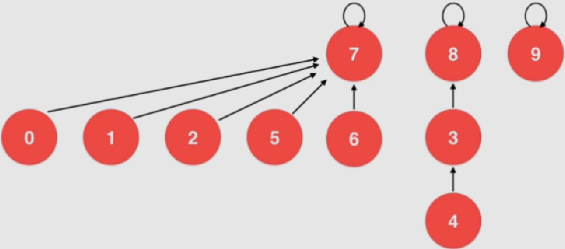
find优化——路径压缩

在find依照节点依次向上寻找根节点时，需要遍历每个节点。如果在这个过程中对树进行一些变化：

  1. 如果在向上寻找的过程中没有找到根节点的话就将当前节点向上挪动

如下述过程中（find元素4）会将整棵树改为右侧的样子：

find元素4

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
namespace UF5{
    class UnionFind{
    private:
        // rank[i]表示以i为根的集合所表示的树的层数
        // 在后续的代码中, 我们并不会维护rank的语意, 也就是rank的值在路径压缩的过程中, 有可能不在是树的层数值
        // 这也是rank不叫height或者depth的原因, 他只是作为比较的一个标准
        int* rank;
        int* parent; // parent[i]表示第i个元素所指向的父节点
        int count;   // 数据个数

    public:
        // 构造函数
        UnionFind(int count){
            parent = new int[count];
            rank = new int[count];
            this->count = count;
            for( int i = 0 ; i < count ; i ++ ){
                parent[i] = i;
                rank[i] = 1;
            }
        }

        // 析构函数
        ~UnionFind(){
            delete[] parent;
            delete[] rank;
        }

        // 查找过程, 查找元素p所对应的集合编号
        // O(h)复杂度, h为树的高度
        int find(int p){
            assert( p >= 0 && p < count );

            // path compression 1
            while( p != parent[p] ){
                parent[p] = parent[parent[p]];//仅仅这一句即可 根节点指向自己，所以无需考虑根节点的情况
                p = parent[p];
            }
            return p;

            // path compression 2, 递归算法
//            if( p != parent[p] )
//                parent[p] = find( parent[p] );//将路径压缩到极致，压缩之后的树只需一步即可找到根节点
//            return parent[p];//此时parent[p]即为根节点
        }

        // 查看元素p和元素q是否所属一个集合
        // O(h)复杂度, h为树的高度
        bool isConnected( int p , int q ){
            return find(p) == find(q);
        }

        // 合并元素p和元素q所属的集合
        // O(h)复杂度, h为树的高度
        void unionElements(int p, int q){

            int pRoot = find(p);
            int qRoot = find(q);

            if( pRoot == qRoot )
                return;

            // 根据两个元素所在树的元素个数不同判断合并方向
            // 将元素个数少的集合合并到元素个数多的集合上
            if( rank[pRoot] < rank[qRoot] ){
                parent[pRoot] = qRoot;
            }
            else if( rank[qRoot] < rank[pRoot]){
                parent[qRoot] = pRoot;
            }
            else{ // rank[pRoot] == rank[qRoot]
                parent[pRoot] = qRoot;
                rank[qRoot] += 1;   // 此时, 我维护rank的值
            }
        }
    };
}

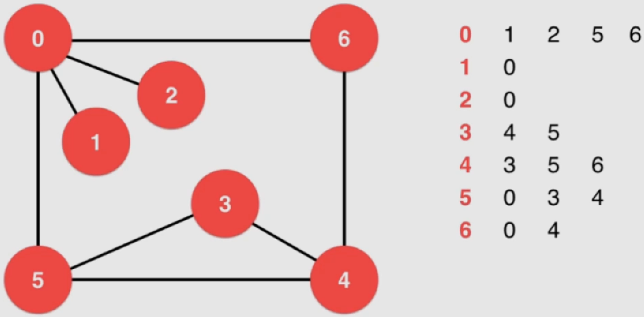
六、无权图

图的表示

实质是对边的描述，通常分为两种：

  1. 邻接矩阵：适合表示稠密图（边相对节点较多）
    • 优：自动解决平行边的问题
    • 缺：遍历领边较慢
  2. 邻接表：适合表示稀疏图（边相对节点较少）
    • 优：遍历领边较快
    • 缺：不能够自动解决平行边，寻找平行边耗时太高

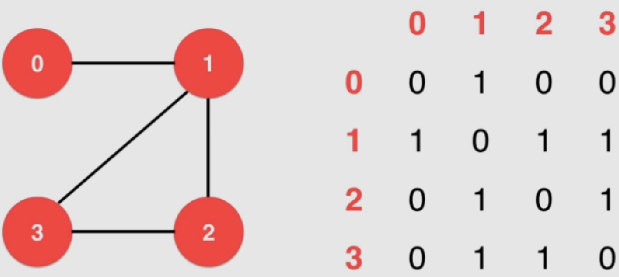
邻接矩阵（稠密）

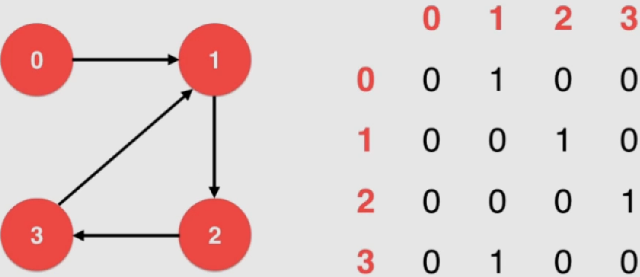
使用一个2*2的矩阵来表示，图中有n个节点则一共有n行n列，设该矩阵位矩阵A，则中AijA_{ij}表示 ii、jj 这两个节点是否相连

  • 对于无向图来说直接表示即可：

邻接矩阵（无向图）表示形式

  • 对于有向图来说，AijA_{ij}表示 ii 节点到 jj 节点是否相连

邻接矩阵（有向图）表示形式

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
// 稠密图 - 邻接矩阵
class DenseGraph{
private:
    int n, m;       // 节点数和边数
    bool directed;  // 是否为有向图
    vector<vector<bool>> g; // 图的具体数据

public:
    // 构造函数
    DenseGraph( int n , bool directed ){
        assert( n >= 0 );
        this->n = n;
        this->m = 0;    // 初始化没有任何边
        this->directed = directed;
        // g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false, 表示没有任和边
        g = vector<vector<bool>>(n, vector<bool>(n, false));
    }

    ~DenseGraph(){ }

    int V(){ return n;} // 返回节点个数
    int E(){ return m;} // 返回边的个数

    // 向图中添加一个边
    void addEdge( int v , int w ){

        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );

        if( hasEdge( v , w ) )
            return;

        g[v][w] = true;
        if( !directed )
            g[w][v] = true;

        m ++;
    }

    // 验证图中是否有从v到w的边
    bool hasEdge( int v , int w ){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
        return g[v][w];
    }
};
  • 通过if( hasEdge( v , w ) )能够顺带处理了平行边的问题
  • 能够用 O(1)O(1) 的速度来判断 v、w 之间是否有边
遍历领边

对于邻接矩阵来说，遍历领边需要花费较高的时间

实现（为了不暴露类中的图，只向用户提供一个接口，这里用迭代器实现）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// 稠密图 - 邻接矩阵
class DenseGraph{
private:
	...
    
public:
    ...

    // 邻边迭代器, 传入一个图和一个顶点,
    // 迭代在这个图中和这个顶点向连的所有顶点
    class adjIterator{
    private:
        DenseGraph &G;  // 图G的引用
        int v;
        int index;

    public:
        // 构造函数
        adjIterator(DenseGraph &graph, int v): G(graph){
            assert( v >= 0 && v < G.n );
            this->v = v;
            this->index = -1;   // 索引从-1开始, 因为每次遍历都需要调用一次next()
        }

        ~adjIterator(){}

        // 返回图G中与顶点v相连接的第一个顶点
        int begin(){

            // 索引从-1开始, 因为每次遍历都需要调用一次next()
            index = -1;
            return next();
        }

        // 返回图G中与顶点v相连接的下一个顶点
        int next(){

            // 从当前index开始向后搜索, 直到找到一个g[v][index]为true
            for( index += 1 ; index < G.V() ; index ++ )
                if( G.g[v][index] )
                    return index;
            // 若没有顶点和v相连接, 则返回-1
            return -1;
        }

        // 查看是否已经迭代完了图G中与顶点v相连接的所有顶点
        bool end(){
            return index >= G.V();
        }
    };
};

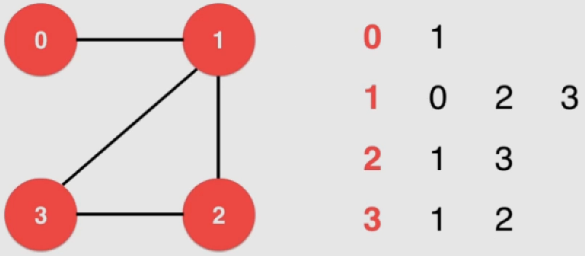
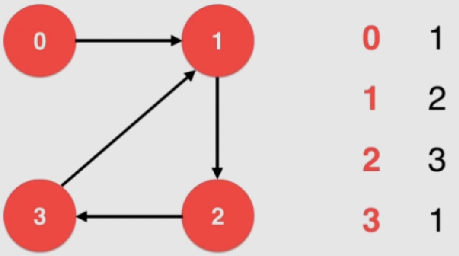
邻接表（稀疏）

对于每一行来说，只表达和该行对应的点连接的那个点的信息：

邻接表（无向图）

  • 第0行：只有1一个元素，表示只和节点1相接

邻接表（有向图）

  • 第0行：只连接1号节点，方向为0–>1

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
// 稀疏图 - 邻接表
class SparseGraph{
private:
    int n, m;       // 节点数和边数
    bool directed;  // 是否为有向图
    vector<vector<int>> g;  // 图的具体数据

public:
    // 构造函数
    SparseGraph( int n , bool directed ){
        assert( n >= 0 );
        this->n = n;
        this->m = 0;    // 初始化没有任何边
        this->directed = directed;
        // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
        g = vector<vector<int>>(n, vector<int>());
    }

    ~SparseGraph(){ }

    int V(){ return n;} // 返回节点个数
    int E(){ return m;} // 返回边的个数

    // 向图中添加一个边
    void addEdge( int v, int w ){

        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );

        g[v].push_back(w);
        if( v != w && !directed ) // 排除自环边：自己指向自己
            g[w].push_back(v);

        m ++;
    }

    // 验证图中是否有从v到w的边
    bool hasEdge( int v , int w ){

        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );

        for( int i = 0 ; i < g[v].size() ; i ++ )
            if( g[v][i] == w )
                return true;
        return false;
    }
};
  • 可以用链表来实现——删除元素是更加方便
  • 这里不涉及删除操作，简单点就使用vector
  • addEdge中由于时间问题暂时不处理平行边的问题
    • 通常是通过整张图构建完毕后再一次性过滤平行边，来排除这个问题
  • 判断 v、w 之间是否 有边时最差能达到 O(n2)O(n^2)
遍历领边

每行中就是领边，所以花费时间较少

实现（为了不暴露类中的图，只向用户提供一个接口，这里用迭代器实现）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// 稀疏图 - 邻接表
class SparseGraph{
private:
    ...

public:
    ...

    // 邻边迭代器, 传入一个图和一个顶点,
    // 迭代在这个图中和这个顶点向连的所有顶点
    class adjIterator{
    private:
        SparseGraph &G; // 图G的引用
        int v;
        int index;

    public:
        // 构造函数
        adjIterator(SparseGraph &graph, int v): G(graph){
            this->v = v;
            this->index = 0;
        }

        ~adjIterator(){}

        // 返回图G中与顶点v相连接的第一个顶点
        int begin(){
            index = 0;
            if( G.g[v].size() )
                return G.g[v][index];
            // 若没有顶点和v相连接, 则返回-1
            return -1;
        }

        // 返回图G中与顶点v相连接的下一个顶点
        int next(){
            index ++;
            if( index < G.g[v].size() )
                return G.g[v][index];
            // 若没有顶点和v相连接, 则返回-1
            return -1;
        }

        // 查看是否已经迭代完了图G中与顶点v相连接的所有顶点
        bool end(){
            return index >= G.g[v].size();
        }
    };
};

遍历

深度优先遍历

时间复杂度（与广度优先遍历一样）：

  • 稀疏图（邻接表）：O(V+E)O(V+E)，通常领边较少，可以认为为O(V)O(V)
    • V：节点个数
    • E：领边条数
  • 稠密图（邻接矩阵）：O(V2)O(V^2)

深度优先遍历

  1. 从节点0开始访问，在第一行中先访问节点1
    1. 节点1连通的只有节点0，且刚刚访问完毕了，退回上一层
  2. 访问节点2
    1. 节点2连通的只有节点0，且刚刚访问完毕了，退回上一层
  3. 访问节点5
    1. 访问节点0，遍历过，继续遍历
    2. 访问节点3
      1. 访问节点4
        1. 访问节点3，遍历过，继续遍历
        2. 访问节点5，遍历过，继续遍历
        3. 访问节点6
          1. 访问节点0，遍历过，继续遍历
          2. 访问节点4，遍历过，返回上一层
      2. 访问节点5，遍历过，返回上一层
    3. 访问节点4，遍历过，返回上一层
  4. 访问节点6，遍历过。
  5. 至此已经全部遍历完毕
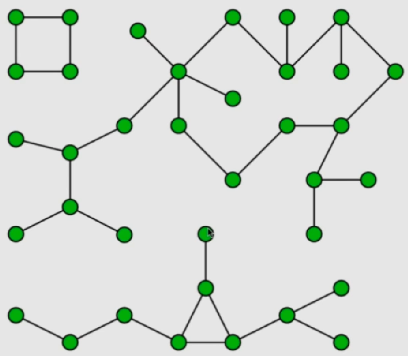
连通分量

典型应用：求图中的连通分量

3个连通分量

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
// 求无权图的联通分量
template <typename Graph>//邻接矩阵 或 连接邻接表
class Component{
private:
    Graph &G;       // 图的引用
    bool *visited;  // 记录dfs的过程中节点是否被访问
    int ccount;     // 记录联通分量个数
    int *id;        // 每个节点所对应的联通分量标记（并查集思想 Quick Find结构）

    // 图的深度优先遍历
    void dfs( int v ){//遍历一个连通分量，并置位每个被访问节点的visited

        visited[v] = true;
        id[v] = ccount;
        typename Graph::adjIterator adj(G, v);//图class中的迭代器，遍历领边
        for( int i = adj.begin() ; !adj.end() ; i = adj.next() ){
            if( !visited[i] )
                dfs(i);
        }
    }

public:
    // 构造函数, 求出无权图的联通分量
    Component(Graph &graph): G(graph){
        // 算法初始化
        visited = new bool[G.V()];//G.V()：图中节点个数
        id = new int[G.V()];
        ccount = 0;
        for( int i = 0 ; i < G.V() ; i ++ ){
            visited[i] = false;// 全部没有访问过
            id[i] = -1;
        }

        // 求图的联通分量
        for( int i = 0 ; i < G.V() ; i ++ )
            if( !visited[i] ){
                dfs(i);
                ccount ++;//dfs后一定含有一个连通分量
            }
    }

    // 析构函数
    ~Component(){
        delete[] visited;
        delete[] id;
    }

    // 返回图的联通分量个数
    int count(){
        return ccount;
    }

    // 查询点v和点w是否联通
    bool isConnected( int v , int w ){
        assert( v >= 0 && v < G.V() );
        assert( w >= 0 && w < G.V() );
        return id[v] == id[w];
    }
};
寻路

在遍历的过程中存储对应的路径（每个节点从哪里遍历过来的）即可，但是并不能保证是最短路径

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
// 路径查询
template <typename Graph>
class Path{
private:
    Graph &G;   // 图的引用
    int s;      // 起始点
    bool* visited;  // 记录dfs的过程中节点是否被访问
    int * from;     // 记录路径, from[i]表示查找的路径上i的上一个节点

    // 图的深度优先遍历
    void dfs( int v ){
        visited[v] = true;

        typename Graph::adjIterator adj(G, v);//遍历领边
        for( int i = adj.begin() ; !adj.end() ; i = adj.next() ){
            if( !visited[i] ){
                from[i] = v;
                dfs(i);
            }
        }
    }

public:
    // 构造函数, 寻路算法, 寻找图graph从s点到其他点的路径
    Path(Graph &graph, int s):G(graph){
        // 算法初始化
        assert( s >= 0 && s < G.V() );

        visited = new bool[G.V()];
        from = new int[G.V()];
        for( int i = 0 ; i < G.V() ; i ++ ){
            visited[i] = false;
            from[i] = -1;
        }
        this->s = s;

        // 寻路算法
        dfs(s);
    }

    // 析构函数
    ~Path(){
        delete [] visited;
        delete [] from;
    }

    // 查询从s点到w点是否有路径
    bool hasPath(int w){
        assert( w >= 0 && w < G.V() );
        return visited[w];
    }

    // 查询从s点到w点的路径, 存放在vec中
    void path(int w, vector<int> &vec){
        assert( hasPath(w) );

        stack<int> s;
        // 通过from数组逆向查找到从s到w的路径, 存放到栈中
        int p = w;
        while( p != -1 ){
            s.push(p);
            p = from[p];
        }

        // 从栈中依次取出元素, 获得顺序的从s到w的路径
        vec.clear();
        while( !s.empty() ){
            vec.push_back( s.top() );
            s.pop();
        }
    }

    // 打印出从s点到w点的路径
    void showPath(int w){
        assert( hasPath(w) );

        vector<int> vec;
        path( w , vec );
        for( int i = 0 ; i < vec.size() ; i ++ ){
            cout<<vec[i];
            if( i == vec.size() - 1 )
                cout<<endl;
            else
                cout<<" -> ";
        }
    }
};

广度优先遍历

类似于树的广度遍历，这里也需要一个队列来临时存储

时间复杂度（与深度优先遍历一样）：

  • 稀疏图（邻接表）：O(V+E)O(V+E)，通常领边较少，可以认为为O(V)O(V)
    • V：节点个数
    • E：领边条数
  • 稠密图（邻接矩阵）：O(V2)O(V^2)

广度优先遍历

  1. 将初始节点0推入队列q中
  2. 将队列首部元素节点0取出，即遍历了节点0，将节点0的领边相连的节点加入队列，此时队列中有节点1、2、5、6
  3. 将队列首部元素节点1取出，即遍历了节点1，将节点1的领边相连的节点加入队列，发现节点0已经遍历，此时队列中有节点2、5、6
  4. 将队列首部元素节点2取出，即遍历了节点2，将节点2的领边相连的节点加入队列，发现节点0已经遍历，此时队列中有节点5、6
  5. 将队列首部元素节点5取出，即遍历了节点5，将节点5的领边相连的节点加入队列，发现节点0已经遍历，此时队列中有节点6、3、4
  6. 将队列首部元素节点6取出，即遍历了节点6，将节点6的领边相连的节点加入队列，发现节点0已经遍历且节点4已经在队列中，此时队列中有节点3、4
  7. 将队列首部元素节点3取出，即遍历了节点3，将节点3的领边相连的节点加入队列，发现节点5已经遍历且节点4已经在队列中，此时队列中有节点4
  8. 将队列首部元素节点4取出，即遍历了节点4，将节点4的领边相连的节点加入队列，发现节点3、5、6已经遍历，此时队列中为空，遍历结束

特点：先遍历的节点距起始节点的距离一定是小于等于后遍历的节点的，所以广度优先遍历求出了无权图的最短路径

最短路径

注意：

  1. 深度优先的结果有时候也是最短路径，具体还是需要看节点的添加方式，即最终的邻接表
  2. 当有多条最短路径时，下面实现的结果取决于遍历顺序（只能输出一条最短路径）

通过上面的思路，有：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
// 寻找无权图的最短路径
template <typename Graph>
class ShortestPath{
private:
    Graph &G;       // 图的引用
    int s;          // 起始点
    bool *visited;  // 记录dfs的过程中节点是否被访问
    int *from;      // 记录路径, from[i]表示查找的路径上i的上一个节点
    int *ord;       // 记录路径中节点的次序。ord[i]表示i节点在路径中的次序。（或离起始点的最短距离）

public:
    // 构造函数, 寻找无权图graph从s点到其他点的最短路径
    ShortestPath(Graph &graph, int s):G(graph){
        // 算法初始化
        assert( s >= 0 && s < graph.V() );

        visited = new bool[graph.V()];
        from = new int[graph.V()];
        ord = new int[graph.V()];
        for( int i = 0 ; i < graph.V() ; i ++ ){
            visited[i] = false;
            from[i] = -1;
            ord[i] = -1;
        }
        this->s = s;

        // 无向图最短路径算法, 从s开始广度优先遍历整张图
        queue<int> q;

        q.push( s );
        visited[s] = true;
        ord[s] = 0;
        while( !q.empty() ){// 只要队列不为空 就一直广度遍历
            int v = q.front();//取出队列首节点
            q.pop();

            typename Graph::adjIterator adj(G, v);//遍历队列首的领边对应的节点
            for( int i = adj.begin() ; !adj.end() ; i = adj.next() )
                if( !visited[i] ){
                    q.push(i);// 新节点 加入到队列中
                    visited[i] = true;
                    from[i] = v;
                    ord[i] = ord[v] + 1;
                }
        }
    }

    // 析构函数
    ~ShortestPath(){
        delete [] visited;
        delete [] from;
        delete [] ord;
    }

    // 查询从s点到w点是否有路径
    bool hasPath(int w){
        assert( w >= 0 && w < G.V() );
        return visited[w];
    }

    // 查询从s点到w点的路径, 存放在vec中
    void path(int w, vector<int> &vec){
        assert( w >= 0 && w < G.V() );

        stack<int> s;
        // 通过from数组逆向查找到从s到w的路径, 存放到栈中
        int p = w;
        while( p != -1 ){
            s.push(p);
            p = from[p];
        }

        // 从栈中依次取出元素, 获得顺序的从s到w的路径
        vec.clear();
        while( !s.empty() ){
            vec.push_back( s.top() );
            s.pop();
        }
    }

    // 打印出从s点到w点的路径
    void showPath(int w){
        assert( w >= 0 && w < G.V() );

        vector<int> vec;
        path(w, vec);
        for( int i = 0 ; i < vec.size() ; i ++ ){
            cout<<vec[i];
            if( i == vec.size()-1 )
                cout<<endl;
            else
                cout<<" -> ";
        }
    }

    // 查看从s点到w点的最短路径长度
    int length(int w){
        assert( w >= 0 && w < G.V() );
        return ord[w];
    }
};

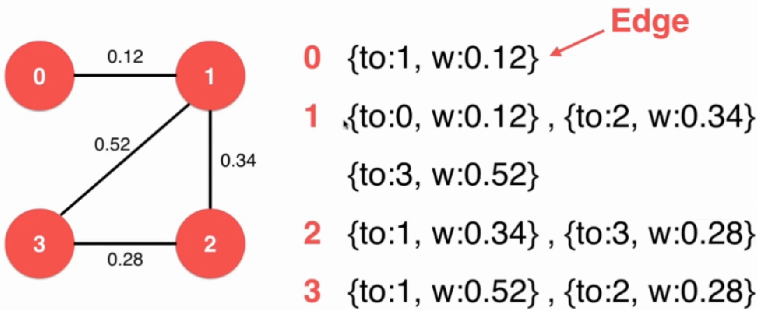
七、有权图

有权图在每条边上都会有一组权重，对于

  • 邻接矩阵：将 Ai,jA_{i,j} 改为权值即可，表示从 ii 到 jj 节点的权值
  • 邻接表：之前每行只用一个值存储连接的节点信息，现在需要两个，即
    1. 相应的索引——即之前存储的值
    2. 对应的权值

邻接表

  • 代码中，边通过指针的形式存储

实现：

边的抽象：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
template<typename Weight>
class Edge{
private:
    int a,b;    // 边的两个端点
    Weight weight;  // 边的权值

public:
    // 构造函数
    Edge(int a, int b, Weight weight){
        this->a = a;
        this->b = b;
        this->weight = weight;
    }
    // 空的构造函数, 所有的成员变量都取默认值
    Edge(){}

    ~Edge(){}

    int v(){ return a;} // 返回第一个顶点
    int w(){ return b;} // 返回第二个顶点
    Weight wt(){ return weight;}    // 返回权值

    // 给定一个顶点, 返回另一个顶点
    int other(int x){
        assert( x == a || x == b );
        return x == a ? b : a;
    }

    // 输出边的信息
    friend ostream& operator<<(ostream &os, const Edge &e){
        os<<e.a<<"-"<<e.b<<": "<<e.weight;
        return os;
    }

    // 边的大小比较, 是对边的权值的大小比较
    bool operator<(Edge<Weight>& e){
        return weight < e.wt();
    }
    bool operator<=(Edge<Weight>& e){
        return weight <= e.wt();
    }
    bool operator>(Edge<Weight>& e){
        return weight > e.wt();
    }
    bool operator>=(Edge<Weight>& e){
        return weight >= e.wt();
    }
    bool operator==(Edge<Weight>& e){
        return weight == e.wt();
    }
};

稠密图——邻接矩阵：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
template <typename Weight>
class DenseGraph{
private:
    int n, m;       // 节点数和边数
    bool directed;  // 是否为有向图
    vector<vector<Edge<Weight> *>> g;   // 图的具体数据（存放指针）

public:
    // 构造函数
    DenseGraph( int n , bool directed){
        assert( n >= 0 );
        this->n = n;
        this->m = 0;
        this->directed = directed;
        // g初始化为n*n的矩阵, 每一个g[i][j]指向一个边的信息, 初始化为NULL
        g = vector<vector<Edge<Weight> *>>(n, vector<Edge<Weight> *>(n, NULL));
    }

    // 析构函数
    ~DenseGraph(){
        for( int i = 0 ; i < n ; i ++ )
            for( int j = 0 ; j < n ; j ++ )
                if( g[i][j] != NULL )
                    delete g[i][j];
    }

    int V(){ return n;} // 返回节点个数
    int E(){ return m;} // 返回边的个数

    // 向图中添加一个边, 权值为weight
    void addEdge( int v, int w , Weight weight ){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );

        // 如果从v到w已经有边, 删除这条边
        if( hasEdge( v , w  ) ){
            delete  g[v][w];//删除之前的边
            if( v != w && !directed )
                delete g[w][v];
            m --;
        }

        g[v][w] = new Edge<Weight>(v, w, weight);
        if( v != w && !directed )
            g[w][v] = new Edge<Weight>(w, v, weight);
        m ++;
    }

    // 验证图中是否有从v到w的边
    bool hasEdge( int v , int w ){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
        return g[v][w] != NULL;//判断是否为空
    }

    // 显示图的信息
    void show(){
        for( int i = 0 ; i < n ; i ++ ){
            for( int j = 0 ; j < n ; j ++ )
                if( g[i][j] )
                    cout<<g[i][j]->wt()<<"\t";
                else
                    cout<<"NULL\t";
            cout<<endl;
        }
    }

    // 邻边迭代器, 传入一个图和一个顶点,
    // 迭代在这个图中和这个顶点向连的所有边
    class adjIterator{
    private:
        DenseGraph &G;  // 图G的引用
        int v;
        int index;

    public:
        // 构造函数
        adjIterator(DenseGraph &graph, int v): G(graph){
            this->v = v;
            this->index = -1;   // 索引从-1开始, 因为每次遍历都需要调用一次next()
        }

        ~adjIterator(){}

        // 返回图G中与顶点v相连接的第一个边
        Edge<Weight>* begin(){
            // 索引从-1开始, 因为每次遍历都需要调用一次next()
            index = -1;
            return next();
        }

        // 返回图G中与顶点v相连接的下一个边
        Edge<Weight>* next(){
            // 从当前index开始向后搜索, 直到找到一个g[v][index]为true
            for( index += 1 ; index < G.V() ; index ++ )
                if( G.g[v][index] )
                    return G.g[v][index];
            // 若没有顶点和v相连接, 则返回NULL
            return NULL;
        }

        // 查看是否已经迭代完了图G中与顶点v相连接的所有边
        bool end(){
            return index >= G.V();//G.g[v].size() ?
        }
    };
};
  • 边通过一个二维指针数组来表示

稀疏图 - 邻接表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
template<typename Weight>
class SparseGraph{
private:
    int n, m;       // 节点数和边数
    bool directed;  // 是否为有向图
    vector<vector<Edge<Weight> *> > g;   // 图的具体数据

public:
    // 构造函数
    SparseGraph( int n , bool directed){
        assert(n >= 0);
        this->n = n;
        this->m = 0;    // 初始化没有任何边
        this->directed = directed;
        // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
        g = vector<vector<Edge<Weight> *> >(n, vector<Edge<Weight> *>());
    }

    // 析构函数
    ~SparseGraph(){
        for( int i = 0 ; i < n ; i ++ )
            for( int j = 0 ; j < g[i].size() ; j ++ )
                delete g[i][j];
    }

    int V(){ return n;} // 返回节点个数
    int E(){ return m;} // 返回边的个数

    // 向图中添加一个边, 权值为weight
    void addEdge( int v, int w , Weight weight){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );

        // 注意, 由于在邻接表的情况, 查找是否有重边需要遍历整个链表
        // 我们的程序允许重边的出现

        g[v].push_back(new Edge<Weight>(v, w, weight));
        if( v != w && !directed )
            g[w].push_back(new Edge<Weight>(w, v, weight));
        m ++;
    }

    // 验证图中是否有从v到w的边
    bool hasEdge( int v , int w ){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
        for( int i = 0 ; i < g[v].size() ; i ++ )
            if( g[v][i]->other(v) == w )// edge中的other:判断与v相接的另一个顶点是否为w
                return true;
        return false;
    }

    // 显示图的信息
    void show(){
        for( int i = 0 ; i < n ; i ++ ){
            cout<<"vertex "<<i<<":\t";
            for( int j = 0 ; j < g[i].size() ; j ++ )
                cout<<"( to:"<<g[i][j]->w()<<",wt:"<<g[i][j]->wt()<<")\t";
            cout<<endl;
        }
    }

    // 邻边迭代器, 传入一个图和一个顶点,
    // 迭代在这个图中和这个顶点向连的所有边
    class adjIterator{
    private:
        SparseGraph &G; // 图G的引用
        int v;
        int index;

    public:
        // 构造函数
        adjIterator(SparseGraph &graph, int v): G(graph){
            this->v = v;
            this->index = 0;
        }

        ~adjIterator(){}

        // 返回图G中与顶点v相连接的第一个边
        Edge<Weight>* begin(){
            index = 0;
            if( G.g[v].size() )
                return G.g[v][index];
            // 若没有顶点和v相连接, 则返回NULL
            return NULL;
        }

        // 返回图G中与顶点v相连接的下一个边
        Edge<Weight>* next(){
            index += 1;
            if( index < G.g[v].size() )
                return G.g[v][index];
            return NULL;
        }

        // 查看是否已经迭代完了图G中与顶点v相连接的所有顶点
        bool end(){
            return index >= G.g[v].size();
        }
    };
};

最小生成树

最小生成树（Minimum Span Tree，MST）：对于一个完全连通的带权图来说，需要找到一个这个图所属的生成树（生成树：一张图如果有v个节点，则使用v-1条边连接的这v个节点所形成的树），且这棵树上的所有边上的权值相加为最小

生成树

该问题通常针对带权无向图、连通图

通常用切分定理来解决该问题，一般有两种算法：

  1. Prim算法
  2. Kruskal算法

切分定理

切分（Cut）：将图中的节点分为两部分，这样一分后，则说这个图形成了两个切分。

横切边（ Crossing Edge）：如果一个边的两个端点，属于切分不同的两边，这个边称为横切边。

切分定理：在一张图中给定任意切分，横切边中权值最小的边必然属于最小生成树。

切分定理

注意：如果横切边有相等的边，根据下面的每一个算法的不同实现，使得结果会有所不同，且下述的每种算法都只能找到其中的一个最小生成树

Lazy Prim算法

Lazy Prim算法

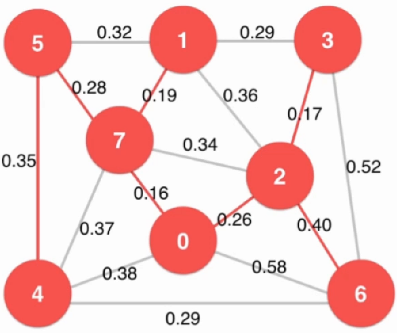
  1. 选定起始点0，与剩下节点做切分，分成两部分
  2. 使用[最小堆](# 1.最大堆)结构从堆中选出最短边
    • 注意：有可能取出的最短边不是横切边，此情况需要排除，见步骤4
  3. 将上述选出的最短边加入节点0的切分中来，重新形成切分与新的横切边
  4. 重新上述1-3步，直到取出的最短边的两个顶点均为节点0的切分内部的边时（不属于横切边），舍弃该边，重新寻找，直至算法完成。如下图为舍弃时的情况

寻找时舍弃内部边

  • 淡蓝色边：横切边
  • 红色边：寻找到的边
  • 上方三条灰色边：舍弃的边

算法时间复杂度：O(ElogE)O(ElogE)

  • E：整个图的所有边的数量

实现：

最小堆：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
template<typename Item>
class MinHeap{
private:
    Item *data;
    int count;
    int capacity;

    void shiftUp(int k){
        while( k > 1 && data[k/2] > data[k] ){
            swap( data[k/2], data[k] );
            k /= 2;
        }
    }

    void shiftDown(int k){
        while( 2*k <= count ){
            int j = 2*k;
            if( j+1 <= count && data[j+1] < data[j] ) j ++;
            if( data[k] <= data[j] ) break;
            swap( data[k] , data[j] );
            k = j;
        }
    }

public:
    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    MinHeap(int capacity){
        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }

    // 构造函数, 通过一个给定数组创建一个最小堆
    // 该构造堆的过程, 时间复杂度为O(n)
    MinHeap(Item arr[], int n){
        data = new Item[n+1];
        capacity = n;

        for( int i = 0 ; i < n ; i ++ )
            data[i+1] = arr[i];
        count = n;

        for( int i = count/2 ; i >= 1 ; i -- )
            shiftDown(i);
    }

    ~MinHeap(){
        delete[] data;
    }

    // 返回堆中的元素个数
    int size(){
        return count;
    }

    // 返回一个布尔值, 表示堆中是否为空
    bool isEmpty(){
        return count == 0;
    }

    // 向最小堆中插入一个新的元素 item
    void insert(Item item){
        assert( count + 1 <= capacity );
        data[count+1] = item;
        shiftUp(count+1);
        count ++;
    }

    // 从最小堆中取出堆顶元素, 即堆中所存储的最小数据
    Item extractMin(){
        assert( count > 0 );
        Item ret = data[1];
        swap( data[1] , data[count] );
        count --;
        shiftDown(1);
        return ret;
    }

    // 获取最小堆中的堆顶元素
    Item getMin(){
        assert( count > 0 );
        return data[1];
    }
};

求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
// 使用Prim算法求图的最小生成树
template<typename Graph, typename Weight>
class LazyPrimMST{
private:
    Graph &G;                   // 图的引用
    MinHeap<Edge<Weight>> pq;   // 最小堆, 算法辅助数据结构
    bool *marked;               // 标记数组, 在算法运行过程中标记节点i是否被访问（切分区）
    vector<Edge<Weight>> mst;   // 最小生成树所包含的所有边
    Weight mstWeight;           // 最小生成树的累计总权值

    // 访问节点v（辅助函数）
    void visit(int v){
        assert( !marked[v] );
        marked[v] = true;// 标记，即代表访问过 或 切分到最小生成树节点区域

        // 将和节点v相连接的所有未访问的边放入最小堆中
        typename Graph::adjIterator adj(G,v);
        for( Edge<Weight>* e = adj.begin() ; !adj.end() ; e = adj.next() )//遍历图中所有边
            if( !marked[e->other(v)] )//e->other(v)：节点v相连的另一个节点 判断此节点是否已经访问过
                pq.insert(*e);// 最小堆中插入该边
    }

public:
    // 构造函数, 使用Prim算法求图的最小生成树
    LazyPrimMST(Graph &graph):G(graph), pq(MinHeap<Edge<Weight>>(graph.E())){//最小堆pq大小默认为整个图中边的数量
        // 算法初始化
        marked = new bool[G.V()];
        for( int i = 0 ; i < G.V() ; i ++ )
            marked[i] = false;
        mst.clear();

        // Lazy Prim
        visit(0);
        while( !pq.isEmpty() ){
            // 使用最小堆找出已经访问的边中权值最小的边
            Edge<Weight> e = pq.extractMin();
            // 如果这条边的两端都已经访问过了, 则扔掉这条边
            if( marked[e.v()] == marked[e.w()] )
                continue;
            // 否则, 这条边则应该存在在最小生成树中（此时该边一定为横切边）
            mst.push_back( e );

            // 访问和这条边连接的还没有被访问过的节点（定为横切边）
            if( !marked[e.v()] )
                visit( e.v() );
            else
                visit( e.w() );
        }

        // 计算最小生成树的权值
        mstWeight = mst[0].wt();
        for( int i = 1 ; i < mst.size() ; i ++ )
            mstWeight += mst[i].wt();
    }

    // 析构函数
    ~LazyPrimMST(){
        delete[] marked;
    }

    // 返回最小生成树的所有边
    vector<Edge<Weight>> mstEdges(){
        return mst;
    };

    // 返回最小生成树的权值
    Weight result(){
        return mstWeight;
    };
};
Prim算法

该算法是Lazy Prim算法的优化版本

算法时间复杂度：O(ElogV)O(ElogV)

  • E：整个图的所有边的数量
  • V：整个图的节点数量
  • 由于整个遍历过程少了，节省的时间非常可观

lazy prim算法缺点：

  1. 所有边都需要经过最小堆，其中有些边随着切分的改变会变为不是横切边
  2. 虽然有很多横切边，但是通常只关注最短的那一条横切边

优化思路：

  1. 使用新的数据结构来维护横切边，存储每个节点相连的最短的横切边
  2. 在不断变化的切分中，只需要不断更新该数据机构即可

满足上述两点的数据结构：[索引堆](# 6.索引堆)

优化后的Prim算法

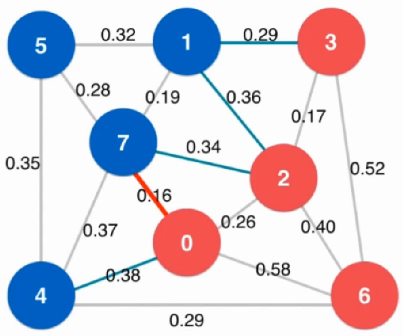
  • 通过一个数组来保存最短临边
  • 从节点0开始，其余节点2、4、6、7临边依次更新进数组，并选出最短临边0.16（节点7）
  • 由0、7组成的切分继续扩充横切边
    • 遍历节点7的临边，未在表中的直接加入，已在表中的判断是否最小值，表中仅仅保留最小值
  • 重复上述步骤直至所有节点全部更新完毕

实现：

最小索引堆：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
template<typename Item>
class IndexMinHeap{
private:
    Item *data;     // 最小索引堆中的数据
    int *indexes;   // 最小索引堆中的索引, indexes[x] = i 表示索引i在x的位置
    int *reverse;   // 最小索引堆中的反向索引, reverse[i] = x 表示索引i在x的位置

    int count;
    int capacity;

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftUp( int k ){
        while( k > 1 && data[indexes[k/2]] > data[indexes[k]] ){
            swap( indexes[k/2] , indexes[k] );
            reverse[indexes[k/2]] = k/2;
            reverse[indexes[k]] = k;
            k /= 2;
        }
    }

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftDown( int k ){
        while( 2*k <= count ){
            int j = 2*k;
            if( j + 1 <= count && data[indexes[j]] > data[indexes[j+1]] )
                j += 1;

            if( data[indexes[k]] <= data[indexes[j]] )
                break;

            swap( indexes[k] , indexes[j] );
            reverse[indexes[k]] = k;
            reverse[indexes[j]] = j;
            k = j;
        }
    }

public:
    // 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
    IndexMinHeap(int capacity){

        data = new Item[capacity+1];
        indexes = new int[capacity+1];
        reverse = new int[capacity+1];

        for( int i = 0 ; i <= capacity ; i ++ )
            reverse[i] = 0;

        count = 0;
        this->capacity = capacity;
    }

    ~IndexMinHeap(){
        delete[] data;
        delete[] indexes;
        delete[] reverse;
    }

    // 返回索引堆中的元素个数
    int size(){
        return count;
    }

    // 返回一个布尔值, 表示索引堆中是否为空
    bool isEmpty(){
        return count == 0;
    }

    // 向最小索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
    // 传入的i对用户而言,是从0索引的
    void insert(int index, Item item){
        assert( count + 1 <= capacity );
        assert( index + 1 >= 1 && index + 1 <= capacity );

        index += 1;
        data[index] = item;
        indexes[count+1] = index;
        reverse[index] = count+1;
        count++;
        shiftUp(count);
    }

    // 从最小索引堆中取出堆顶元素, 即索引堆中所存储的最小数据
    Item extractMin(){
        assert( count > 0 );

        Item ret = data[indexes[1]];
        swap( indexes[1] , indexes[count] );
        reverse[indexes[count]] = 0;
        reverse[indexes[1]] = 1;
        count--;
        shiftDown(1);
        return ret;
    }

    // 从最小索引堆中取出堆顶元素的索引
    int extractMinIndex(){
        assert( count > 0 );

        int ret = indexes[1] - 1;
        swap( indexes[1] , indexes[count] );
        reverse[indexes[count]] = 0;
        reverse[indexes[1]] = 1;
        count--;
        shiftDown(1);
        return ret;
    }

    // 获取最小索引堆中的堆顶元素
    Item getMin(){
        assert( count > 0 );
        return data[indexes[1]];
    }

    // 获取最小索引堆中的堆顶元素的索引
    int getMinIndex(){
        assert( count > 0 );
        return indexes[1]-1;
    }

    // 看索引i所在的位置是否存在元素
    bool contain( int index ){

        return reverse[index+1] != 0;
    }

    // 获取最小索引堆中索引为i的元素
    Item getItem( int index ){
        assert( contain(index) );
        return data[index+1];
    }

    // 将最小索引堆中索引为i的元素修改为newItem
    void change( int index , Item newItem ){

        assert( contain(index) );
        index += 1;
        data[index] = newItem;

        shiftUp( reverse[index] );
        shiftDown( reverse[index] );
    }
};

求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
// 使用优化的Prim算法求图的最小生成树
template<typename Graph, typename Weight>
class PrimMST{
private:
    Graph &G;                     // 图的引用
    IndexMinHeap<Weight> ipq;     // 最小索引堆, 算法辅助数据结构
    vector<Edge<Weight>*> edgeTo; // 访问的点所对应的最短横切边, 算法辅助数据结构
    bool* marked;                 // 标记数组, 在算法运行过程中标记节点i是否被访问
    vector<Edge<Weight>> mst;     // 最小生成树所包含的所有边
    Weight mstWeight;             // 最小生成树的权值

    // 访问节点v
    void visit(int v){
        assert( !marked[v] );
        marked[v] = true;

        // 将和节点v相连接的未访问的另一端点, 和与之相连接的边, 放入最小堆中
        typename Graph::adjIterator adj(G,v);
        for( Edge<Weight>* e = adj.begin() ; !adj.end() ; e = adj.next() ){//遍历节点v的临边
            int w = e->other(v);
            // 如果边的另一端点未被访问（即横切边）
            if( !marked[w] ){
                // 如果从没有考虑过这个端点, 直接将这个端点和与之相连接的边加入索引堆
                if( !edgeTo[w] ){
                    edgeTo[w] = e;
                    ipq.insert(w, e->wt());
                }
                // 如果曾经考虑这个端点, 但现在的边比之前考虑的边更短, 则进行替换
                else if( e->wt() < edgeTo[w]->wt() ){
                    edgeTo[w] = e;// 存储最短横切边
                    ipq.change(w, e->wt());
                }
            }
        }

    }
public:
    // 构造函数, 使用Prim算法求图的最小生成树
    PrimMST(Graph &graph):G(graph), ipq(IndexMinHeap<double>(graph.V())){
        assert( graph.E() >= 1 );

        // 算法初始化
        marked = new bool[G.V()];
        for( int i = 0 ; i < G.V() ; i ++ ){
            marked[i] = false;
            edgeTo.push_back(NULL);
        }
        mst.clear();

        // Prim
        visit(0);
        while( !ipq.isEmpty() ){
            // 使用最小索引堆找出已经访问的边中权值最小的边
            // 最小索引堆中存储的是点的索引, 通过点的索引找到相对应的边
            int v = ipq.extractMinIndex();
            assert( edgeTo[v] );//确保节点v的最小横切边存在
            mst.push_back( *edgeTo[v] );
            visit( v );
        }
	    //求解累计权值	
        mstWeight = mst[0].wt();
        for( int i = 1 ; i < mst.size() ; i ++ )
            mstWeight += mst[i].wt();
    }

    ~PrimMST(){
        delete[] marked;
    }

    vector<Edge<Weight>> mstEdges(){
        return mst;
    };

    Weight result(){
        return mstWeight;
    };
};
Kruskal算法

依次找到图中的最短的边，只要这些边之间不构成一个环，则一定是最小生成树中相应的边

Kruskal算法

  1. 将所有边从小到大进行排序
  2. 选取最小边进行判断，若不会形成环则为最小生成树的边
    • 判断是否为环这个操作可以通过并查集来实现
  3. 重复上述1-2步，直至找到n-1条边，其中n为节点个数

时间复杂度：O(ElogE)O(ElogE)，较上述两种算法耗时，但是实现较为简单

  • E：整个图的所有边的数量

实现：

并查集：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
// Quick Union + rank + path compression
class UnionFind{
private:
    // rank[i]表示以i为根的集合所表示的树的层数
    // 在后续的代码中并不会维护rank的语意, 也就是rank的值在路径压缩的过程中, 有可能不在是树的层数值
    // 这也是我们的rank不叫height或者depth的原因, 他只是作为比较的一个标准
    int* rank;
    int* parent; // parent[i]表示第i个元素所指向的父节点
    int count;   // 数据个数

public:
    // 构造函数
    UnionFind(int count){
        parent = new int[count];
        rank = new int[count];
        this->count = count;
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            rank[i] = 1;
        }
    }

    // 析构函数
    ~UnionFind(){
        delete[] parent;
        delete[] rank;
    }

    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    int find(int p){
        assert( p >= 0 && p < count );

        // path compression 1
        while( p != parent[p] ){
            parent[p] = parent[parent[p]];
            p = parent[p];
        }
        return p;

        // path compression 2, 递归算法
//            if( p != parent[p] )
//                parent[p] = find( parent[p] );
//            return parent[p];
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    bool isConnected( int p , int q ){
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    void unionElements(int p, int q){

        int pRoot = find(p);
        int qRoot = find(q);

        if( pRoot == qRoot )
            return;

        // 根据两个元素所在树的元素个数不同判断合并方向
        // 将元素个数少的集合合并到元素个数多的集合上
        if( rank[pRoot] < rank[qRoot] ){
            parent[pRoot] = qRoot;
        }
        else if( rank[qRoot] < rank[pRoot]){
            parent[qRoot] = pRoot;
        }
        else{ // rank[pRoot] == rank[qRoot]
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;   // 此时, 需要维护rank的值
        }
    }
};

Kruskal算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
template <typename Graph, typename Weight>
class KruskalMST{
private:
    vector<Edge<Weight>> mst;   // 最小生成树所包含的所有边
    Weight mstWeight;           // 最小生成树的权值
public:
    // 构造函数, 使用Kruskal算法计算graph的最小生成树
    KruskalMST(Graph &graph){
        // 将图中的所有边存放到一个最小堆中（并排序）
        MinHeap<Edge<Weight>> pq( graph.E() );
        for( int i = 0 ; i < graph.V() ; i ++ ){
            typename Graph::adjIterator adj(graph,i);
            for( Edge<Weight> *e = adj.begin() ; !adj.end() ; e = adj.next() )
                if( e->v() < e->w() )// 防止每条边被正向、反向遍历两边
                    pq.insert(*e);
        }

        // 创建一个并查集, 来查看已经访问的节点的联通情况
        UnionFind uf = UnionFind(graph.V());
        while( !pq.isEmpty() && mst.size() < graph.V() - 1 ){

            // 从最小堆中依次从小到大取出所有的边
            Edge<Weight> e = pq.extractMin();
            // 如果该边的两个端点是联通的, 说明加入这条边将产生环, 扔掉这条边
            if( uf.isConnected( e.v() , e.w() ) )
                continue;

            // 否则, 将这条边添加进最小生成树, 同时标记边的两个端点联通
            mst.push_back( e );
            uf.unionElements( e.v() , e.w() );
        }
	    //求和
        mstWeight = mst[0].wt();
        for( int i = 1 ; i < mst.size() ; i ++ )
            mstWeight += mst[i].wt();
    }

    ~KruskalMST(){ }

    // 返回最小生成树的所有边
    vector<Edge<Weight>> mstEdges(){
        return mst;
    };

    // 返回最小生成树的权值
    Weight result(){
        return mstWeight;
    };
};

Vyssotsky算法

基本思想：将任意一条边逐渐地添加到生成树中，一旦形成环，删除环中权值最大的边

该算法需要删除边、且需要在环上的最长边（需要探测环的存在且找到环中权值最大的边），对于这个操作暂时没有优秀的数据结构能够快速的处理该事，所以一般实现较为复杂

八、最短路径

对于无向图、有向图均成立

最短路径问题：求从一个节点到另一个节点耗费最小的路径

对于一个无权图，从某个一节点开始进行广度优先遍历，结果其实就是求从一个节点到其他所有节点相应的最短路径，其实这形成了从起始节点开始到其他所有节点的一棵树，通常称之为最短路径树（Shortest Path Tree），求这棵树的过程通常称之为单源最短路径（Single Source Shortest Path）

松弛(relaxation)：指对于图 G=(V,E)G = (V, E) 中每个顶点 v∈Vv ∈ V ，都设置一个属性 dist[v]dist[v] ，用来描述从源点 ss 到 vv 的最短路径上权值的上界。在开始进行一个最短路径算法时，只知道图中边和权值。随着算法的进行，逐渐得到各对顶点的最短路径的信息。算法会逐渐更新这些信息，每步都会检查是否可以找到一条路径比当前给定路径更短。这一过程通常称为松弛。

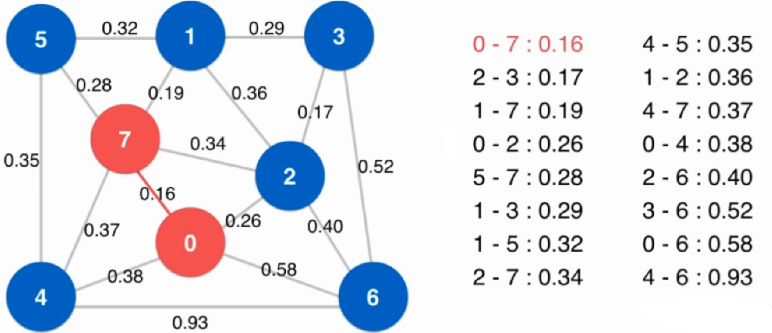
dijkstra单源最短路径算法

前提：图中不能有负权边

在最优的情况下时间复杂度为：O(ElogV)O(ElogV)

  • E：整个图的所有边的数量
  • V：整个图的节点数量

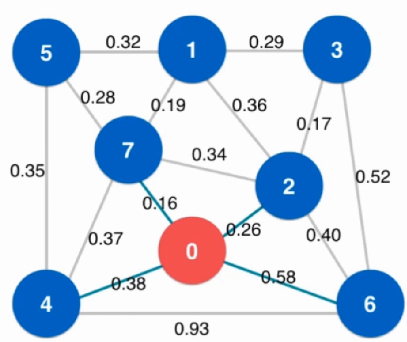
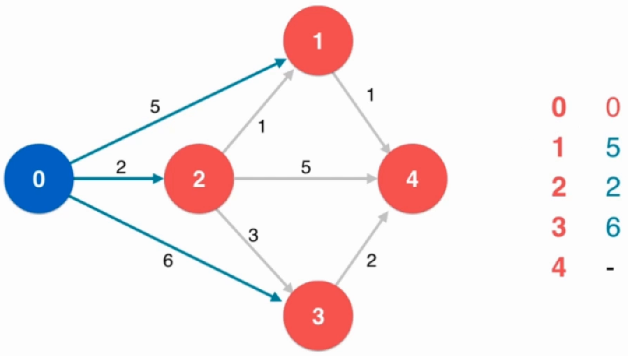
dijkstra算法

  • 选定初始点：节点0，标出节点0的所有临边
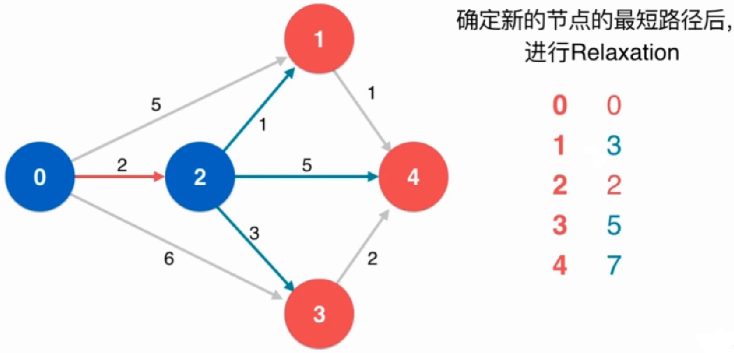
  • 找到未访问节点中能够以最短路径访问的节点，即节点2
    • 因为没有负权，且到其他节点的距离都>2，所以不可能有比2更短的距离到节点2

松弛操作

  • 进行松弛操作：从节点2开始到其他节点有没有可能比 已经找到的、从原点到其他节点 路径更短的路线
    • 由于0-2-1比之前的0-1路径短，所以在表中更新（即松弛过程）
    • 由于0-2-3比之前的0-3路径短，所以在表中更新（即松弛过程）
  • 由于之前没有到过节点4，所以表中直接填
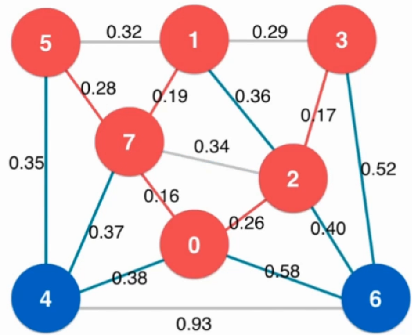
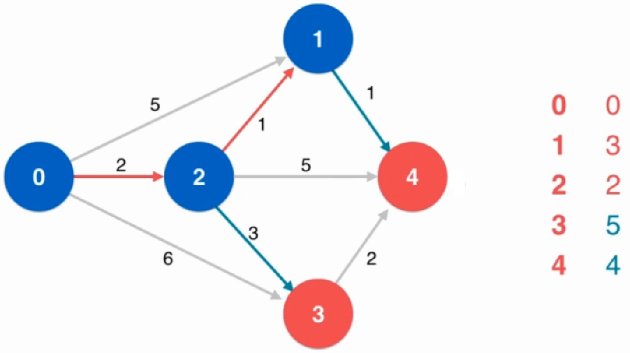
  • 重复上述循环：找到此时未访问节点中能够以最短路径访问的节点，即节点1

重复

  • 进行松弛操作：从节点1开始到其他节点有没有可能比 已经找到的、从原点到其他节点 路径更短的路线
    • 由于0-2-1-4比之前的0-2-4路径短，所以在表中更新（即松弛过程）
  • 重复上述循环：找到此时未访问节点中能够以最短路径访问的节点，即节点4
  • 最后只剩下节点3，此时长度就为5，至此算法结束

实现：

最小索引堆：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
template<typename Item>
class IndexMinHeap{
private:
    Item *data;     // 最小索引堆中的数据
    int *indexes;   // 最小索引堆中的索引, indexes[x] = i 表示索引i在x的位置
    int *reverse;   // 最小索引堆中的反向索引, reverse[i] = x 表示索引i在x的位置

    int count;
    int capacity;

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftUp( int k ){

        while( k > 1 && data[indexes[k/2]] > data[indexes[k]] ){
            swap( indexes[k/2] , indexes[k] );
            reverse[indexes[k/2]] = k/2;
            reverse[indexes[k]] = k;
            k /= 2;
        }
    }

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftDown( int k ){

        while( 2*k <= count ){
            int j = 2*k;
            if( j + 1 <= count && data[indexes[j]] > data[indexes[j+1]] )
                j += 1;

            if( data[indexes[k]] <= data[indexes[j]] )
                break;

            swap( indexes[k] , indexes[j] );
            reverse[indexes[k]] = k;
            reverse[indexes[j]] = j;
            k = j;
        }
    }

public:
    // 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
    IndexMinHeap(int capacity){

        data = new Item[capacity+1];
        indexes = new int[capacity+1];
        reverse = new int[capacity+1];

        for( int i = 0 ; i <= capacity ; i ++ )
            reverse[i] = 0;

        count = 0;
        this->capacity = capacity;
    }

    ~IndexMinHeap(){
        delete[] data;
        delete[] indexes;
        delete[] reverse;
    }

    // 返回索引堆中的元素个数
    int size(){
        return count;
    }

    // 返回一个布尔值, 表示索引堆中是否为空
    bool isEmpty(){
        return count == 0;
    }

    // 向最小索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
    // 传入的i对用户而言,是从0索引的
    void insert(int index, Item item){
        assert( count + 1 <= capacity );
        assert( index + 1 >= 1 && index + 1 <= capacity );

        index += 1;
        data[index] = item;
        indexes[count+1] = index;
        reverse[index] = count+1;
        count++;
        shiftUp(count);
    }

    // 从最小索引堆中取出堆顶元素, 即索引堆中所存储的最小数据
    Item extractMin(){
        assert( count > 0 );

        Item ret = data[indexes[1]];
        swap( indexes[1] , indexes[count] );
        reverse[indexes[count]] = 0;
        reverse[indexes[1]] = 1;
        count--;
        shiftDown(1);
        return ret;
    }

    // 从最小索引堆中取出堆顶元素的索引
    int extractMinIndex(){
        assert( count > 0 );

        int ret = indexes[1] - 1;
        swap( indexes[1] , indexes[count] );
        reverse[indexes[count]] = 0;
        reverse[indexes[1]] = 1;
        count--;
        shiftDown(1);
        return ret;
    }

    // 获取最小索引堆中的堆顶元素
    Item getMin(){
        assert( count > 0 );
        return data[indexes[1]];
    }

    // 获取最小索引堆中的堆顶元素的索引
    int getMinIndex(){
        assert( count > 0 );
        return indexes[1]-1;
    }

    // 看索引i所在的位置是否存在元素
    bool contain( int index ){

        return reverse[index+1] != 0;
    }

    // 获取最小索引堆中索引为i的元素
    Item getItem( int index ){
        assert( contain(index) );
        return data[index+1];
    }

    // 将最小索引堆中索引为i的元素修改为newItem
    void change( int index , Item newItem ){

        assert( contain(index) );
        index += 1;
        data[index] = newItem;

        shiftUp( reverse[index] );
        shiftDown( reverse[index] );
    }
};

Dijkstra算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
template<typename Graph, typename Weight>
class Dijkstra{
private:
    Graph &G;                   // 图的引用
    int s;                      // 起始点
    Weight *distTo;             // distTo[i]存储从起始点s到i的最短路径长度
    bool *marked;               // 标记数组, 在算法运行过程中标记节点i是否被访问
    vector<Edge<Weight>*> from; // from[i]记录最短路径中, 到达i点的边是哪一条边
                                // 可以用来恢复整个最短路径

public:
    // 构造函数, 使用Dijkstra算法求最短路径
    Dijkstra(Graph &graph, int s):G(graph){
        // 算法初始化
        assert( s >= 0 && s < G.V() );
        this->s = s;
        distTo = new Weight[G.V()];
        marked = new bool[G.V()];
        for( int i = 0 ; i < G.V() ; i ++ ){
            distTo[i] = Weight();// 调用模板的默认构造函数
            marked[i] = false;
            from.push_back(NULL);
        }

        // 使用索引堆记录当前找到的到达每个顶点的最短距离
        IndexMinHeap<Weight> ipq(G.V());

        // 对于其实点s进行初始化
        distTo[s] = Weight();// 调用模板的默认构造函数
        from[s] = new Edge<Weight>(s, s, Weight());
        ipq.insert(s, distTo[s] );
        marked[s] = true;
        while( !ipq.isEmpty() ){
            int v = ipq.extractMinIndex();//取出最小索引堆中距原点最近的点

            // distTo[v]就是s到v的最短距离
            marked[v] = true;

            // 对v的所有相邻节点进行更新（核心操作——松弛操作）
            typename Graph::adjIterator adj(G, v);
            for( Edge<Weight>* e = adj.begin() ; !adj.end() ; e = adj.next() ){//对v邻边进行遍历
                int w = e->other(v);//找到邻边的另一个节点w
                // 如果从s点到w点的最短路径还没有找到
                if( !marked[w] ){//松弛操作
                    // 如果w点以前没有访问过,
                    // 或者访问过, 但是通过当前的v点到w点距离更短, 则进行更新
                    if( from[w] == NULL || distTo[v] + e->wt() < distTo[w] ){
                        distTo[w] = distTo[v] + e->wt();
                        from[w] = e;
                        if( ipq.contain(w) )//维护最小索引堆
                            ipq.change(w, distTo[w] );//如果包含该节点，则更新最小距离
                        else
                            ipq.insert(w, distTo[w] );//否则直接插入
                    }
                }
            }
        }
    }

    // 析构函数
    ~Dijkstra(){
        delete[] distTo;
        delete[] marked;
        delete from[s];
    }

    // 返回从s点到w点的最短路径长度
    Weight shortestPathTo( int w ){
        assert( w >= 0 && w < G.V() );
        assert( hasPathTo(w) );
        return distTo[w];
    }

    // 判断从s点到w点是否联通
    bool hasPathTo( int w ){
        assert( w >= 0 && w < G.V() );
        return marked[w];
    }

    // 寻找从s到w的最短路径, 将整个路径经过的边存放在vec中
    void shortestPath( int w, vector<Edge<Weight>> &vec ){
        assert( w >= 0 && w < G.V() );
        assert( hasPathTo(w) );

        // 通过from数组逆向查找到从s到w的路径, 存放到栈中
        stack<Edge<Weight>*> s;
        Edge<Weight> *e = from[w];
        while( e->v() != this->s ){//不是原点
            s.push(e);//放入栈中
            e = from[e->v()];//取出上一条边
        }
        s.push(e);//存入最后一条边

        // 从栈中依次取出元素, 获得顺序的从s到w的路径
        while( !s.empty() ){
            e = s.top();
            vec.push_back( *e );
            s.pop();
        }
    }

    // 打印出从s点到w点的路径
    void showPath(int w){
        assert( w >= 0 && w < G.V() );
        assert( hasPathTo(w) );

        vector<Edge<Weight>> vec;
        shortestPath(w, vec);
        for( int i = 0 ; i < vec.size() ; i ++ ){
            cout<<vec[i].v()<<" -> ";
            if( i == vec.size()-1 )
                cout<<vec[i].w()<<endl;
        }
    }
};

Bellman-Ford单源最短路径算法

dijkstra算法的缺点就是不能够处理负权边

负权环：从某一点到该点的一个环，环上权重和为负数。

当一个图中出现负权环，则不存在最短路径或最短路径为−∞-\infty

前提：图中不能有负权环，若图中有负权环，该算法虽然找不到最短路径，但是可以判断是否有负权环

基本思想：如果一个图没有负权环，从一点到另外一点的最短路径，最多经过所有的V个顶点（一个图中假设有V个顶点），有V-1条边。否则，存在顶点经过了两次，既存在负权环

注意：在无向图中，只要有一条负权边，即可认为有一个负权环

时间复杂度：O(EV)O(EV)

  • E：整个图的所有边的数量
  • V：整个图的节点数量

松弛操作

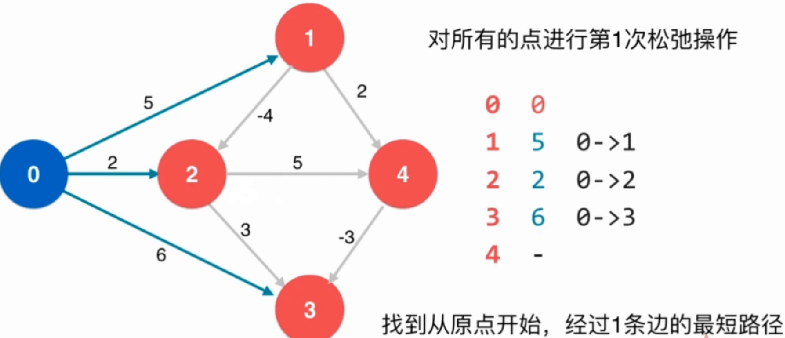
  1. 找到初始节点0相邻的所有邻边，即可暂时找到和其他节点之间的一个路径，且暂时得到一个最短路径
    • 上述操作可以视为对节点0相邻的所有节点进行了一次松弛操作，得到的结果是从原点开始经过一条边到其他节点的最短路径
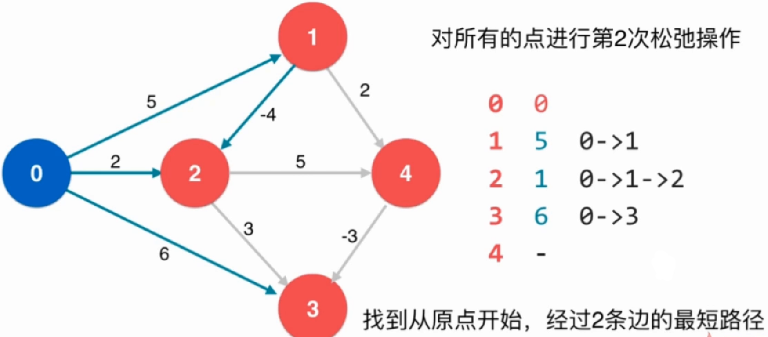
  2. 在进行一次松弛操作：

第二次松弛操作

  • 再次松弛操作后，能够找到从原点开始通过两条路径的最短路径

综上：对所有的点进行V-1次松弛操作，理论上就找到了从源点到其他所有点的最短路径。如果还可以继续松弛，所说原图中有负权环。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
// 使用BellmanFord算法求最短路径
template <typename Graph, typename Weight>
class BellmanFord{
private:
    Graph &G;                   // 图的引用
    int s;                      // 起始点
    Weight* distTo;             // distTo[i]存储从起始点s到i的最短路径长度
    vector<Edge<Weight>*> from; // from[i]记录最短路径中, 到达i点的边是哪一条边
                                // 可以用来恢复整个最短路径
    bool hasNegativeCycle;      // 标记图中是否有负权环

    // 判断图中是否有负权环（继续松弛操作）
    bool detectNegativeCycle(){
        for( int i = 0 ; i < G.V() ; i ++ ){
            typename Graph::adjIterator adj(G,i);
            for( Edge<Weight>* e = adj.begin() ; !adj.end() ; e = adj.next() )
                if( from[e->v()] && distTo[e->v()] + e->wt() < distTo[e->w()] )
                    return true;
        }
        return false;
    }

public:
    // 构造函数, 使用BellmanFord算法求最短路径
    BellmanFord(Graph &graph, int s):G(graph){
        this->s = s;
        distTo = new Weight[G.V()];
        // 初始化所有的节点s都不可达, 由from数组来表示
        for( int i = 0 ; i < G.V() ; i ++ )
            from.push_back(NULL);

        // 设置distTo[s] = 0, 并且让from[s]不为NULL, 表示初始s节点可达且距离为0
        distTo[s] = Weight();
        from[s] = new Edge<Weight>(s, s, Weight()); // 这里我们from[s]的内容是new出来的, 注意要在析构函数里delete掉

        // Bellman-Ford的过程
        // 进行V-1次循环, 每一次循环求出从起点到其余所有点, 最多使用pass步可到达的最短距离
        for( int pass = 1 ; pass < G.V() ; pass ++ ){
            // 每次循环中对所有的边进行一遍松弛操作
            // 遍历所有边的方式是先遍历所有的顶点, 然后遍历和所有顶点相邻的所有边
            for( int i = 0 ; i < G.V() ; i ++ ){
                // 使用邻边迭代器遍历和所有顶点相邻的所有边
                typename Graph::adjIterator adj(G,i);
                for( Edge<Weight>* e = adj.begin() ; !adj.end() ; e = adj.next() )
                    // 对于每一个边首先判断e->v()可达
                    // 之后看如果e->w()以前没有到达过， 显然我们可以更新distTo[e->w()]
                    // 或者e->w()以前虽然到达过, 但是通过这个e我们可以获得一个更短的距离, 即可以进行一次松弛操作, 我们也可以更新distTo[e->w()]
                    if( from[e->v()] && (!from[e->w()] || distTo[e->v()] + e->wt() < distTo[e->w()]) ){
                        distTo[e->w()] = distTo[e->v()] + e->wt();
                        from[e->w()] = e;
                    }
            }
        }

        hasNegativeCycle = detectNegativeCycle();//继续松弛操作，即进行第V次循环，判断是否为负权环
    }

    // 析构函数
    ~BellmanFord(){
        delete[] distTo;
        delete from[s];
    }

    // 返回图中是否有负权环
    bool negativeCycle(){
        return hasNegativeCycle;
    }

    // 返回从s点到w点的最短路径长度
    Weight shortestPathTo( int w ){
        assert( w >= 0 && w < G.V() );
        assert( !hasNegativeCycle );
        assert( hasPathTo(w) );
        return distTo[w];
    }

    // 判断从s点到w点是否联通
    bool hasPathTo( int w ){
        assert( w >= 0 && w < G.V() );
        return from[w] != NULL;
    }

    // 寻找从s到w的最短路径, 将整个路径经过的边存放在vec中
    void shortestPath( int w, vector<Edge<Weight>> &vec ){
        assert( w >= 0 && w < G.V() );
        assert( !hasNegativeCycle );
        assert( hasPathTo(w) );

        // 通过from数组逆向查找到从s到w的路径, 存放到栈中
        stack<Edge<Weight>*> s;
        Edge<Weight> *e = from[w];
        while( e->v() != this->s ){
            s.push(e);
            e = from[e->v()];
        }
        s.push(e);

        // 从栈中依次取出元素, 获得顺序的从s到w的路径
        while( !s.empty() ){
            e = s.top();
            vec.push_back( *e );
            s.pop();
        }
    }

    // 打印出从s点到w点的路径
    void showPath(int w){
        assert( w >= 0 && w < G.V() );
        assert( !hasNegativeCycle );
        assert( hasPathTo(w) );

        vector<Edge<Weight>> vec;
        shortestPath(w, vec);
        for( int i = 0 ; i < vec.size() ; i ++ ){
            cout<<vec[i].v()<<" -> ";
            if( i == vec.size()-1 )
                cout<<vec[i].w()<<endl;
        }
    }
};

思考：最长路径

  • 最长路径问题不能有正权环
  • 无权图的最长路径问题是指数级难度的
  • 对于有权图，不能使用 Dijkstra求最长路径问题
  • 可以使用 Bellman-Ford算法（将权重取负，然后求最短路径）