SVM数学推导

SVM（线性模型）数学推导

作者：zihuanqiu

学习路线：先线性二分类解释清楚，再加入核方法扩展至非线性二分类

几个重要的概念

1. 训练样本集

   $(\boldsymbol{x}_i,y_i)$，其中$\boldsymbol{x_i}$为$n$维列向量，表示$n$维特征；$y_i$为标签，当$y_i=+1$时为正样本，$y_i=-1$时为负样本。

   则训练样本集为：$D=\left\{\left(\boldsymbol{x}_{\boldsymbol{1}},y_1 \right),\left(\boldsymbol{x}_2,y_2\right),\cdots,\left(\boldsymbol{x}_m,y_m\right)\right\},y\in\left\{-1,+1\right\}$

2. 什么叫超平面

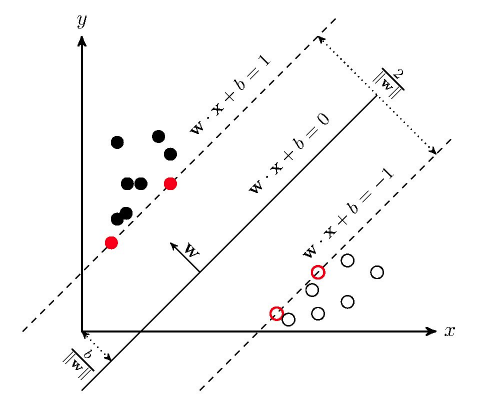
   如上图，若在二维空间内（两个特征），若数据为线性可分，则可以用一条直线将正负样本区分开来（2分类问题）；若在三维空间则为一个平面；三维空间以上无法想象统称为超平面。

   但上图中区分正负样本肯定又不止一种划分方法，何者为最优？最优者才叫做SVM的超平面。

   最优的判断标准则是，若对数据样本加以扰动（可以理解为采样样本总有误差），那么SVM超平面具有最佳的鲁棒性。从几何上来看，在上图中，若将超平面左右平移，直至触碰到最近的样本，那么这个被界定的范围记为$d$，则SVM的超平面是有最大$d$的那个超平面。

3. 什么叫支持向量

   SVM超平面左右平移最先触碰到的为支持向量

4. 超平面的方程

   $\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+b=0$

   其中：$\boldsymbol{w}$和$\boldsymbol{x}$都是$n\times 1$的列向量，$n$是特征维数。$b$为标量；$\boldsymbol{w}$还是超平面的法向量，$b$控制了超平面到原点的距离。确定了$\boldsymbol{w}$和$b$，超平面就被完全确定了。

   那么在超平面上方数据$\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+b>0$；在超平面下方数据$\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+b<0$；

5. $\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+b=0$与$\zeta\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+\zeta b=0$表示的是同一个超平面

   如：$4x+4y=0$ 和 $x+y=0$ 是同一个平面，$4x+4y=4$ 和 $x+y=1$也是同一个平面

6. 线性可分数据集的定义

   在数据集$\left\{ \left( \boldsymbol{x}_i,y_i \right) \right\} _{i=1\sim m}$中，$\exists \left( \boldsymbol{w},b \right)$，使得对于$\forall i=1 \sim m$，有：

   $\begin{cases} \text{若}y_i=+1, \text{则}\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{i}}+b> 0\\ \text{若}y_i=-1, \text{则}\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{i}}+b< 0\\ \end{cases}$

   即正样本全部分到上方，负样本全部分到下方

   等价于 $y_i(\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{i}}+b)> 0$

7. 点到平面距离公式

   点$(x_0,y_0)$到平面$w_1x+w_2y+b=0$的距离表示为：

   $d=\frac{\left| w_1x_0+w_2y_0+b \right|}{\sqrt{w_{1}^{2}+w_{2}^{2}}}$

   则样本点到超平面的距离表示为：

   $d=\frac{\left| \boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{i}}+b \right|}{\lVert \boldsymbol{w} \rVert}$

8. 若假设支持向量过超平面的平行线为$\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+b=1$和$\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+b=-1$（如上图所示），那么可求得

   支持向量到超平面的距离为:

   $d=\frac{1}{\lVert \boldsymbol{w} \rVert}$

   那么超平面左右平移被限制的范围（即两个异类支持向量到超平面的距离之和）为：

   $\varUpsilon =\frac{2}{\lVert \boldsymbol{w} \rVert}$

   $\varUpsilon$被称为SVM的“间隔”（margin）

   为什么可以假设支持向量过超平面的平行线为$\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+b=1$和$\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+b=-1$呢？正如上面第5点所述，由于$\boldsymbol{W}$和$b$可以整体缩放倍数，超平面不变。那么总可以通过$\zeta \cdot \left( \boldsymbol{w},b \right) \rightarrow \left( \boldsymbol{w'},b' \right)$，使$\left| \boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}+b \right|=1$。归一化的操作为我们带来便利

求解超平面转化为下列优化问题

在限制条件 $y_i(w^Tx_i+b)\geqslant 1,i=1\sim m$ 下，最小化 $\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2$ 的问题

即：

$\begin{aligned} &\underset{\boldsymbol{w},b}{\min}\,\,\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2 \\ &s.t.\quad y_i(\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{i}}+b)\geqslant 1,i=1\sim m \end{aligned}$

最大化$\varUpsilon =\frac{2}{\lVert \boldsymbol{w} \rVert}$等价于最小化$\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2$，而限制条件$y_i(w^Tx_i+b)\geqslant 1,i=1\sim m$表示求解超平面的前提条件是所有样本都被正确分类的情况下

这样就把支持向量机的求解转化为凸优化问题中的二次规划问题

二次规划（Quadratic Programming）

1. 目标函数（Objective Function）为二次项
2. 限制条件为一次项

要么无解，要么只有一个极值

SVM（非线性模型）数学推导

若数据集非线性可分，那么线性SVM的优化问题会变得无解。通过加入正则项，可以使SVM应用于非线性可分的数据集。

改写优化目标函数和限制条件

$\begin{aligned} &\underset{\boldsymbol{w},b}{\min}\,\,\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2+C\sum_{i=1}^m{\xi _i}\\ &s.t.\quad \begin{cases} y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{i}}+b \right) \geqslant 1-\xi _i\\ \xi _i\geqslant 0\\ \end{cases},i=1\sim m\\ \end{aligned} \tag{1}$

其中：$\xi_i$称为松弛变量（Slack Variable），$\sum_{i=1}^m{\xi _i}$称为正则项

若$\xi_i$足够大，则限制条件可以被轻易满足（即为限制条件加入了容忍度）。但$\xi_i$又不能太大，那么限制条件就失去了意义。因此在优化目标函数里需要添加$\xi_i$，并用一个超参数$C$来权衡最小化$\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2$与最小化$\sum_{i=1}^m{\xi _i}$之间的关系

低维到高维的映射

改写优化目标函数和限制条件后的SVM可以应用于非线性可分的数据集中。但是这样的SVM仍然是在试图寻找一条直线将正负样本划分，在某些情况下这仍然不够好，例如：

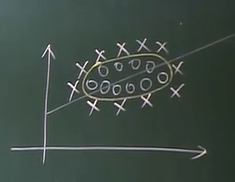
不同于其他机器学习算法，SVM试图通过高维映射，使低维空间的线性不可分问题变成高维空间中的线性可分问题，从而在高维空间中画出超平面对数据集进行划分。

我们定义高维映射$\varphi (\boldsymbol{x})$：

$\boldsymbol{x}\xrightarrow{\varphi }\varphi \left( \boldsymbol{x} \right)$

其中$\boldsymbol{x}$是低维向量，而$\varphi (\boldsymbol{x})$为高维向量

那么SVM的优化条件变为：

$\begin{aligned} &\underset{\boldsymbol{w},b}{\min}\,\,\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2 +C\sum_{i=1}^m{\xi _i} \\ &s.t.\quad \begin{cases} y_i(\boldsymbol{w}^{\boldsymbol{T}}\varphi (\boldsymbol{x}_{\boldsymbol{i}})+b) \geqslant 1-\xi _i\\ \xi _i\geqslant 0\\ \end{cases},i=1\sim m \end{aligned}$

此时$\boldsymbol{w}$的维度也升高了，与$\varphi (\boldsymbol{x})$的维度相同

例子：

对于这么一个异或问题，我们有：

$\begin{aligned} &\boldsymbol{x}_{\boldsymbol{1}}=\left[ \begin{array}{c} 0\\ 0\\ \end{array} \right] \in C_1,\quad \boldsymbol{x}_{\boldsymbol{2}}=\left[ \begin{array}{c} 1\\ 1\\ \end{array} \right] \in C_1,\quad \\ &\boldsymbol{x}_{\boldsymbol{3}}=\left[ \begin{array}{c} 1\\ 0\\ \end{array} \right] \in C_2,\quad \boldsymbol{x}_{\boldsymbol{4}}=\left[ \begin{array}{c} 0\\ 1\\ \end{array} \right] \in C_2 \end{aligned}$

定义映射关系：

$\boldsymbol{x}=\left[ \begin{array}{c} a\\ b\\ \end{array} \right] \xrightarrow{\varphi }\varphi \left( \boldsymbol{x} \right) =\left[ \begin{array}{c} a^2\\ b^2\\ a\\ \begin{array}{c} b\\ ab\\ \end{array}\\ \end{array} \right]$

则升维后的样本为

$\begin{aligned} &\varphi \left( \boldsymbol{x}_{\boldsymbol{1}} \right) =\left[ \begin{array}{c} \begin{array}{c} 0\\ 0\\ \end{array}\\ \begin{array}{c} 0\\ 0\\ 0\\ \end{array}\\ \end{array} \right] \in C_1,\quad \varphi \left( \boldsymbol{x}_{\boldsymbol{2}} \right) =\left[ \begin{array}{c} \begin{array}{c} 1\\ 1\\ \end{array}\\ \begin{array}{c} 1\\ 1\\ 1\\ \end{array}\\ \end{array} \right] \in C_1,\quad \\ &\varphi \left( \boldsymbol{x}_{\boldsymbol{3}} \right) =\left[ \begin{array}{c} \begin{array}{c} 1\\ 0\\ \end{array}\\ \begin{array}{c} 1\\ 0\\ 0\\ \end{array}\\ \end{array} \right] \in C_2,\quad \varphi \left( \boldsymbol{x}_{\boldsymbol{4}} \right) =\left[ \begin{array}{c} \begin{array}{c} 0\\ 1\\ \end{array}\\ \begin{array}{c} 0\\ 1\\ 0\\ \end{array}\\ \end{array} \right] \in C_2 \end{aligned}$

求得$\boldsymbol{w}$为：

$\boldsymbol{w}=\left[ \begin{array}{c} \begin{array}{c} -1\\ -1\\ \end{array}\\ \begin{array}{c} -1\\ -1\\ 6\\ \end{array}\\ \end{array} \right] ,\quad b=1$

则

$\begin{aligned} \widehat{y}_1&=\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{1}}+b\,\,=\,\,1>0\\\widehat{y}_2&=\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{2}}+b\,\,=\,\,3>0\\\widehat{y}_3&=\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{3}}+b\,\,=\,\,-1<0\\\widehat{y}_4&=\boldsymbol{w}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{4}}+b\,\,=\,\,-1<0 \end{aligned}$

可见的确通过升维，在高维空间划分了超平面，实现了非线性可分数据的分类问题。

核函数

可以证明：若升的维度越高，则数据集越有可能在高维空间被线性划分。可以猜想，若$\varphi (\boldsymbol{x})$为无限维度，则必定可以在无限高维空间划分任意数据集。但这样，会使得$\boldsymbol{w}$也变为无限维度，使优化问题$(1)$变得不可解（因为$\boldsymbol{w}$是代求参数）。

定理：我们可以不知道无限维映射$\varphi (\boldsymbol{x})$的显式表达，我们只要知道一个核函数（Kernel Function）

$K\left( \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}} \right) \,\,=\,\,\varphi \left( \boldsymbol{x}_{\boldsymbol{1}} \right) ^T\cdot \varphi \left( \boldsymbol{x}_{\boldsymbol{2}} \right)$

则$(1)$这个优化式仍然可解。

常用核函数：

1. 高斯核

   $K\left( \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}} \right) \,\,=\,\,e^{-\frac{\lVert x_1-x_2 \rVert ^2}{2\sigma ^2}}$

2. 多项式核

$K\left( \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}} \right) \,\,=\,\,\left( \boldsymbol{x}_{\boldsymbol{1}}^{\boldsymbol{T}}\boldsymbol{x}_{\boldsymbol{2}}+1 \right) ^d$

我们知道核$K\left( \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}} \right)$的表达式，且知道$K\left( \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}} \right)$可以表示为$\varphi \left( \boldsymbol{x}_{\boldsymbol{1}} \right) ^T \varphi \left( \boldsymbol{x}_{\boldsymbol{2}} \right)$，并且$\varphi (\boldsymbol{x})$是无限维的（不需要知道$\varphi (\boldsymbol{x})$的显示表达）。

$K\left( \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}} \right)$能写成$\varphi \left( \boldsymbol{x}_{\boldsymbol{1}} \right) ^T \varphi \left( \boldsymbol{x}_{\boldsymbol{2}} \right)$的充要条件为（Mercer’s Theorem）：

1. $K\left( \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}} \right) = K\left( \boldsymbol{x}_{\boldsymbol{2}},\boldsymbol{x}_{\boldsymbol{1}} \right)$（交换性）
2. $\forall C_i, \,\, \boldsymbol{x_i}(i=1\sim N)$，有$\sum_{i=1}^N{\sum_{j=1}^N{C_iC_jK\left( \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}} \right) \geqslant 0}}\,\,$成立（半正定性）

原问题和对偶问题

现在我们要在只知道$K\left( \boldsymbol{x}_{\boldsymbol{1}},\boldsymbol{x}_{\boldsymbol{2}} \right)$不知道$\varphi (\boldsymbol{x})$的情况下，解优化问题$(1)$，因此我们需要一些理论知识铺垫。

这是优化理论的内容，用到就学一下吧

原问题（Prime Problem）：

最小化：

$f(\boldsymbol{\omega})$

限制条件：

$\begin{array}{cc} g_i\left( \boldsymbol{\omega} \right) \leqslant 0 \left( i=1\sim K \right) \\ h_i\left( \boldsymbol{\omega} \right) =0 \left( i=1\sim M \right) \end{array}$

则其对偶问题（Dual Problem）为：

最大化：

$\varTheta \left( \boldsymbol{\alpha} ,\boldsymbol{\beta}\right) \,\,=\,\,\underset{for\,\,all\,\,\boldsymbol{\omega}}{inf}\left\{ L\left( \boldsymbol{\omega} ,\boldsymbol{\alpha} ,\boldsymbol{\beta} \right) \right\}$

限制条件：

$\boldsymbol{\alpha }\geqslant 0$

其中$L\left( \boldsymbol{\omega} ,\boldsymbol{\alpha },\boldsymbol{\beta } \right)$为：

$\begin{aligned} L\left( \boldsymbol{\omega} ,\boldsymbol{\alpha },\boldsymbol{\beta } \right) \,\,&=\,\,f\left( \boldsymbol{\omega} \right) +\sum_{i=1}^K{\alpha _ig_i\left( \boldsymbol{\omega} \right)}+\sum_{i=1}^M{\beta _ih_i\left( \boldsymbol{\boldsymbol{\omega}} \right)}\,\, \\ &=\,\,f\left( \boldsymbol{\omega} \right) +\boldsymbol{\alpha }^{\boldsymbol{T}}g\left( \boldsymbol{\omega} \right) +\boldsymbol{\beta }^{\boldsymbol{T}}h\left( \boldsymbol{\omega} \right) \end{aligned}$

$\underset{for\,\,all\,\,\boldsymbol{\omega}}{inf}$的意思是，在所有$\boldsymbol{\omega}$取值上取得的最小值

原问题和对偶问题的关系：如果$\boldsymbol{\omega}^*$是原问题的解，而$\boldsymbol{\alpha}^*,\boldsymbol{\beta}^*$是对偶问题的解，则有：

$f\left( \boldsymbol{\omega} ^* \right) \geqslant \theta \left( \boldsymbol{\alpha} ^*,\boldsymbol{\beta} ^* \right)$

proof:

$\begin{aligned} \theta \left( \boldsymbol{\alpha }^*,\boldsymbol{\beta }^* \right) \,\,&=\,\,\underset{for\,\,all\,\,\omega}{inf}\left\{ L\left( \boldsymbol{\omega },\boldsymbol{\alpha }^*,\boldsymbol{\beta }^* \right) \right\} \leqslant L\left( \boldsymbol{\omega }^*,\boldsymbol{\alpha }^*,\boldsymbol{\beta }^* \right) \\ &=\,\,f\left( \boldsymbol{\omega }^* \right) +\sum_{i=1}^K{\boldsymbol{\alpha }_{i}^{*}g_i\left( \boldsymbol{\omega }^* \right)}+\sum_{i=1}^M{\boldsymbol{\beta }_{i}^{*}h_i\left( \boldsymbol{\omega }^* \right)}\leqslant \,\,f\left( \boldsymbol{\omega }^* \right) \end{aligned}$

因为其中$\boldsymbol{\alpha^* }\geqslant 0$, $g_i\left( \boldsymbol{\omega ^*} \right) \leqslant 0$，$h_i\left( \boldsymbol{\omega^* } \right) =0$

强对偶定理

若$f(\boldsymbol{\omega})$为凸函数，且$g(\boldsymbol{\omega}) = \boldsymbol{A\omega} + b$，$h(\boldsymbol{\omega}) = \boldsymbol{C\omega} + d$，则优化问题的原问题与对偶问题间距为0，即：

$f\left( \boldsymbol{\omega} ^* \right) = \theta \left( \boldsymbol{\alpha} ^*,\boldsymbol{\beta} ^* \right)$

再观察上面的proof过程，可以立即得出：

对 $\forall i=1 \sim K$，有$\boldsymbol{\alpha^*_i }=0$ 或者 $g_i\left( \boldsymbol{\omega ^*} \right) =0$

以上称为KKT条件

将SVM原问题转化为对偶问题

核函数SVM优化目标可以改写为（为了使形式上靠近优化理论，将$\xi _i\geqslant 0\rightarrow \xi _i\leqslant 0$）

最小化：

$\underset{\boldsymbol{w},b}{\min}\,\,\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2+C\sum_{i=1}^m{\xi _i}\rightarrow \underset{\boldsymbol{w},b}{\min}\,\,\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2-C\sum_{i=1}^m{\xi _i}$

限制条件：

$\begin{aligned} y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b \right) \geqslant 1-\xi _i\,\,&\rightarrow \,\,y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b \right) \geqslant 1+\xi _i\,\, \\ &\rightarrow \,\,1+\xi _i-y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b \right) \leqslant 0 \\ \xi _i\geqslant 0&\rightarrow \xi _i\leqslant 0 \end{aligned}$

1. 原问题	1.核函数SVM原问题
最小化： $f(\boldsymbol{\omega})$	最小化： $\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2-C\sum_{i=1}^m{\xi _i}$
限制条件： $\begin{array}{cc} g_i\left( \boldsymbol{\omega} \right) \leqslant 0 \left( i=1\sim K \right) \\h_i\left( \boldsymbol{\omega} \right) =0 \left( i=1\sim M \right) \end{array}$	限制条件： $\begin{array}{cc} \,1+\xi _i-y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b \right) \leqslant 0 \\ \xi _i\leqslant 0 \end{array}$

从限制条件可知，左边的不等式限制条件$g_i\left( \boldsymbol{\omega} \right) \leqslant 0$对应右边的$\,1+\xi _i-y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b \right) \leqslant 0$和$\xi _i\leqslant 0$；而没有等式限制条。

优化目标函数$f(\boldsymbol{\omega})$对应$\frac{1}{2}\lVert \boldsymbol{w} \rVert ^2+C\sum_{i=1}^m{\xi _i}$

左边只有一个变量$\boldsymbol{\omega}$，而右边对应有三个变量$\boldsymbol{\omega}，\xi _i， b$

因此可以推导出核函数SVM的对偶问题：

2. 对偶问题	2. 核函数SVM对偶问题
最大化： $\varTheta \left( \boldsymbol{\alpha} ,\boldsymbol{\beta}\right) \,=\,\underset{for\,\,all\,\,\boldsymbol{\omega}}{inf}\left\{ L\left( \boldsymbol{\omega} ,\boldsymbol{\alpha} ,\boldsymbol{\beta} \right) \right\}$	最大化： $\begin{aligned}\varTheta\left(\boldsymbol{\alpha },\boldsymbol{\beta}\right)\,=\,\underset{for\,\,all\,\left(\,\boldsymbol{\omega},\xi_i,b\right)}{inf}\left\{\frac{1}{2}\lVert\boldsymbol{w}\rVert^2-C\sum_{i=1}^m{\xi_i}+\sum_{i=1}^m{\alpha_i}\,\left(1+\xi_i-y_i\left(\boldsymbol{w}^{\boldsymbol{T}}\varphi\boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b\right)\right)+\sum_{i=1}^m{\beta_i\xi_i}\right\}\end{aligned}$
限制条件： $\alpha_i\geqslant 0 \quad (i=1 \sim K)$	限制条件： $\alpha_i\geqslant 0 , \beta_i \geqslant 0 \quad(i=1 \sim m)$
$L\left( \boldsymbol{\omega },\boldsymbol{\alpha },\boldsymbol{\beta } \right) \,\,=\,\,f\left( \boldsymbol{\omega } \right) +\sum_{i=1}^K{\alpha _ig_i\left( \boldsymbol{\omega } \right)}+\sum_{i=1}^M{\beta _ih_i\left( \boldsymbol{\omega } \right)}\,\,$

注意，由于SVM中的不等式限制条件有$\alpha_i$和$\beta_i$两个，因此实际上左边的$\alpha_i$对应右边的$\alpha_i$和$\beta_i$

现在我们来求解下式的具体表达式

$\begin{aligned} \varTheta \left( \boldsymbol{\alpha },\boldsymbol{\beta } \right) \,&=\underset{for\,\,all\,\left( \,\boldsymbol{\omega },\xi _i,b \right)}{inf}\left\{ L\left( \boldsymbol{\omega },\boldsymbol{\xi },b \right) \right\} \, \\ &=\underset{for\,\,all\,\left( \,\boldsymbol{\omega },\boldsymbol{\xi },b \right)}{inf}\left\{ \frac{1}{2}\lVert \boldsymbol{w} \rVert ^2-C\sum_{i=1}^m{\xi _i}+\sum_{i=1}^m{\alpha _i}\,\left( 1+\xi _i-y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b \right) \right) +\sum_{i=1}^m{\beta _i\xi _i} \right\} \end{aligned}$

$\underset{for\,\,all\,\left( \,\boldsymbol{\omega },\xi _i,b \right)}{inf}$表示求关于$\left( \,\boldsymbol{\omega },\xi _i,b \right)$的最小值，即求$\frac{\partial}{\partial \boldsymbol{\omega }}L\left( \boldsymbol{\omega },\xi _i,b \right)$，$\frac{\partial}{\partial \xi _i}L\left( \boldsymbol{\omega },\xi _i,b \right)$，$\frac{\partial}{\partial b}L\left( \boldsymbol{\omega },\xi _i,b \right)$，并使他们等于零：

$\begin{aligned} &\frac{\partial}{\partial \boldsymbol{\omega }}L\left( \boldsymbol{\omega },\xi _i,b \right) =0\rightarrow \boldsymbol{\omega }=\sum_{i=1}^m{\alpha _iy_i\varphi \left( x_i \right)}\\ &\frac{\partial}{\partial \xi _i}L\left( \boldsymbol{\omega },\xi _i,b \right) =0\rightarrow \alpha _i+\beta _i=C\\ &\frac{\partial}{\partial b}L\left( \boldsymbol{\omega },\xi _i,b \right) =0\rightarrow \sum_{i=1}^m{\alpha _iy_i=0}\\ \end{aligned} \tag2$

其中用到矩阵求导参考矩阵论，这里给出结果

若$f\left( \boldsymbol{\omega } \right) =\frac{1}{2}\lVert \boldsymbol{\omega } \rVert ^2$，则$\frac{\partial}{\partial \boldsymbol{\omega }}f\left( \boldsymbol{\omega } \right) =\boldsymbol{\omega }$

若$f\left( \boldsymbol{\omega } \right) =\boldsymbol{\omega }^{\text{T}}x$，则$\frac{\partial}{\partial \boldsymbol{\omega }}f\left( \boldsymbol{\omega } \right) =x$

将$(2)$带入$\varTheta \left( \boldsymbol{\alpha },\boldsymbol{\beta } \right)$，得到：

$\varTheta \left( \boldsymbol{\alpha }\right) =\sum_{i=1}^m{\alpha _i-\frac{1}{2}\sum_{i=1}^m{\sum_{j=1}^m{\alpha _i\alpha _jy_iy_j}}}K\left( x_i,x_j \right)$

这时，通过把原问题转换为对偶问题，得到了核函数的表示形式！

将$(2)$带入限制条件$\alpha_i\geqslant 0 , \beta_i \geqslant 0 (i=1 \sim m)$得到：

$\begin{array}{cc} 0\leqslant \alpha _i\leqslant C \\ \sum_{i=1}^m{\alpha _iy_i=0} \end{array}$

于是我们求得了核函数SVM的优化对偶问题

核函数SVM对偶问题
最大化：$\varTheta \left( \boldsymbol{\alpha }\right) =\sum_{i=1}^m{\alpha _i-\frac{1}{2}\sum_{i=1}^m{\sum_{j=1}^m{\alpha _i\alpha _jy_iy_j}}}K\left( x_i,x_j \right)$
限制条件：$0\leqslant \alpha _i\leqslant C \quad\quad \sum_{i=1}^m{\alpha _iy_i=0}$

于是只有一个参数待求解：$\boldsymbol{\alpha}$，通常可以使用SMO算法

在测试流程中，我们可以有如下判断：

$\begin{cases} \text{若}\boldsymbol{w}^{\boldsymbol{T}}\varphi \left( \boldsymbol{x}_{\text{i}} \right) +b>0,\text{则}y_{\text{i}}=+1\\ \text{若}\boldsymbol{w}^{\boldsymbol{T}}\varphi \left( \boldsymbol{x}_{\text{i}} \right) +b<0,\text{则}y_{\text{i}}=-1\\ \end{cases}$

在$(2)$中，我们知道有$\boldsymbol{\omega }=\sum_{i=1}^m{\alpha _iy_i\varphi \left( \boldsymbol{x_i} \right)}$，则：

$\begin{aligned} \boldsymbol{w}^{\boldsymbol{T}}\varphi \left( \boldsymbol{x}_{\boldsymbol{i}} \right) &=\sum_{j=1}^m{\left[ \alpha _iy_i\varphi \left( \boldsymbol{x}_j \right) \right] ^{\text{T}}}\varphi \left( \boldsymbol{x}_{\boldsymbol{i}} \right) \\&=\sum_{j=1}^m{\alpha _iy_i\varphi \left( \boldsymbol{x}_{\boldsymbol{j}} \right) ^{\text{T}}\varphi \left( \boldsymbol{x}_{\boldsymbol{i}} \right)}\\&=\sum_{j=1}^m{\alpha _iy_iK\left( \boldsymbol{x}_{\boldsymbol{i}},\boldsymbol{x}_{\boldsymbol{j}} \right)} \end{aligned} \tag{3}$

只剩下$b$待求解。确定了$b$，则核函数SVM训练完成

$b$的求解需要用到KKT条件，

3. KKT条件	3. SVM的KKT条件
$\forall i=1 \sim K$， $\boldsymbol{\alpha^*_i }=0$ 或者 $g_i\left( \boldsymbol{\omega ^*} \right) =0$	$\forall i=1 \sim m$， 1. $\boldsymbol{\alpha_i }=0$ 或者 $\,1+\xi _i-y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b \right) = 0$ 2. $\boldsymbol{\beta_i }=0$或者$\xi_i=0$

取一个$0<\boldsymbol{\alpha }_{\boldsymbol{i}}<C\Rightarrow \boldsymbol{\beta }_{\boldsymbol{i}}=C-\boldsymbol{\alpha }_{\boldsymbol{i}}>0$，此时有：

$\begin{aligned} \boldsymbol{\beta }_{\boldsymbol{i}}\ne 0&\Rightarrow \xi _i=0 \\ \boldsymbol{\alpha }_{\boldsymbol{i}}\ne 0&\Rightarrow 1+\xi _i-y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b \right) =0 \\ &\Rightarrow 1-y_i\left( \boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}+b \right) =0 \end{aligned}$

带入$(3)$，得到：

$\begin{aligned} b&=\frac{1}{y_i}-\boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}=\frac{1-y_i\boldsymbol{w}^{\boldsymbol{T}}\varphi \boldsymbol{(x}_{\boldsymbol{i}}\text{)}}{y_i} \\ &=\frac{1-y_i\sum_{j=1}^m{\alpha _iy_iK\left( \boldsymbol{x}_{\boldsymbol{i}},\boldsymbol{x}_{\boldsymbol{j}} \right)}}{y_i} \end{aligned}$

以上就是核函数SVM原问题转换为对偶问题，并用对偶问题训练SVM（求出$\boldsymbol{\alpha_i}$和$b$的过程）的推导过程

核函数SVM算法总结

SVM算法

1. 训练流程：

   • 输入${(\boldsymbol{x_i},y_i)}_{i=1 \sim m}$

   • 解优化问题：

     ​ 最大化：$\varTheta \left( \boldsymbol{\alpha }\right) =\sum_{i=1}^m{\alpha _i-\frac{1}{2}\sum_{i=1}^m{\sum_{j=1}^m{\alpha _i\alpha _jy_iy_j}}}K\left( x_i,x_j \right)$

     ​ 限制条件：$0\leqslant \alpha _i\leqslant C, \quad\sum_{i=1}^m{\alpha _iy_i=0}$

     ​ 求解$b$：找一个$0<\boldsymbol{\alpha }_{\boldsymbol{i}}<C$，可以算得$b=\frac{1-y_i\sum_{j=1}^m{\alpha _iy_iK\left( \boldsymbol{x}_{\boldsymbol{i}},\boldsymbol{x}_{\boldsymbol{j}} \right)}}{y_i}$

2. 测试流程

   • 输入测试样本$\boldsymbol{x}$

     $\begin{cases} \text{若}\sum_{j=1}^m\alpha _iy_iK\left( \boldsymbol{x}_{\boldsymbol{i}},\boldsymbol{x}_{\boldsymbol{j}} \right) +b>0,\text{则}y_{\text{i}}=+1\\ \text{若}\sum_{j=1}^m\alpha _iy_iK\left( \boldsymbol{x}_{\boldsymbol{i}},\boldsymbol{x}_{\boldsymbol{j}} \right) +b<0,\text{则}y_{\text{i}}=-1\\ \end{cases}$

通过转换为对偶问题，我们可以看到上面没有出现$\varphi (\boldsymbol{x})$，而待求解的参数只有$\boldsymbol{\alpha_i}$和$b$

SVM处理多分类问题

上面都在说如何用SVM处理二分类问题，那么怎么样用SVM处理多分类问题呢？

我们有一下三种方法：

1. 改造优化的目标函数和限制条件，使之能处理多分类问题。

   这种方法通常效果一般，SVM专为二分类而生

2. 一类VS其他类

   例子：

   若有$C_1 ,C_2 ,C_3$三类，则可以设计三个SVM

   SVM1：$(C_1 ,C_2)VS(C_3)$

   SVM2：$(C_1 ,C_3)VS(C_2)$

   SVM3：$(C_2 ,C_3)VS(C_1)$

   若$y_1=+1,y_2=+1,y_3=-1$，则 显然为第一类

   若$y_1=+1,y_2=-1,y_3=-1$，在看看SVM1和SVM2的$\boldsymbol{w}^{\boldsymbol{T}}\varphi \left( \boldsymbol{x}_{\text{i}} \right) +b$哪一个负的比较多就判断为哪一个

3. 一类VS另一类

   例子：

   若有$C_1 ,C_2 ,C_3$三类，则可以设计三个SVM

   SVM1：$(C_1 )VS(C_2)$

   SVM2：$(C_1 )VS(C_3)$

   SVM3：$(C_2)VS(C_3)$

   若$y_1=+1,y_2=+1,y_3=-1$，则 显然为第一类（$C_1$被投了两票，$C_3$被投了一票）

对于n分类问题：

用一类VS其他类我们需要用n个SVM；

用一类VS另一类我们需要用$\frac{n\left( n-1 \right)}{2}$个SVM。

根据经验，用一类VS另一类的效果最佳，但同时也是最复杂的。